扩展热阻(2)-二维情况下的解析解
扩展热阻(2)-二维情况的解析解
扩展热阻(1)里介绍了三维情况的解析解,这里推导一下二维情况的解析解。
问题陈述
系统的控制方程为拉普拉斯方程:
\[ \nabla^{2} \theta=\frac{\partial^{2} \theta}{\partial x^{2}}+\frac{\partial^{2} \theta}{\partial z^{2}}=0 \]
在顶部存在热源的区域,满足等热流边界条件:
\[ \left.\frac{\partial \theta}{\partial z}\right|_{z=0}=-\frac{\left(Q / A_{s}\right)}{k_{1}} \]
其中\(A_s = c\),在热源区域外,满足:
\[ \left.\frac{\partial \theta}{\partial z}\right|_{z=0}=0 \]
底部满足对流换热边界条件:
\[ \left.\frac{\partial \theta}{\partial z}\right|_{z=t_{1}}=-\frac{h}{k_{1}}\theta(x,t_1) \]
侧边界为绝热边界条件:
\[ \begin{aligned} &\left.\frac{\partial \theta}{\partial x}\right|_{x=0, a}=0 \\ \end{aligned} \]
通解
首先采用分离变量法求解拉普拉斯方程:
\[ \nabla^{2} \theta=\frac{\partial^{2} \theta}{\partial x^{2}}+\frac{\partial^{2} \theta}{\partial z^{2}}=0 \]
设解的形式为:
\[ \theta(x,z) = X(x)Z(z) \]
代入:
\[ \frac{1}{X(x)}\frac{\partial ^2 \theta}{\partial x^2} + \frac{1}{Z(z)}\frac{\partial ^2 \theta}{\partial z^2} = 0 \]
一个是\(x\)的函数,一个是\(z\)的函数,于是设:
\[ \begin{aligned} \frac{1}{X(x)}\frac{\partial ^2 \theta}{\partial x^2} &= - \lambda^2 \\ \frac{1}{Z(z)}\frac{\partial ^2 \theta}{\partial z^2} &= \lambda^2 \\ \end{aligned} \]
- 当\(\lambda < 0\)时,满足边界条件的解无意义
- 当\(\lambda = 0\)时,此时
\[ X = C_0x + C_1 \]
代入绝热边界条件后,得到:
\[ X = C_1 \]
此时
\[ Z = C_2z + C_3 \]
- 当\(\lambda > 0\)时,此时
\[ X = C_0 \sin(\lambda x) + C_1 \cos(\lambda x) \]
代入绝热边界条件后,得到:
\[ \begin{aligned} X &= C_1 \cos(\lambda x), \lambda_n = \frac{n\pi}{a}, n = 1,2,\ldots \\ Z &= C_2 e^{\lambda z} + C_3 e^{-\lambda z} \end{aligned} \]
根据叠加原理,可以得到最终解的形式为:
\[ \theta = A_0 + B_0 z + \sum_{n=1}^{\infty} \cos(\lambda_n x) \left( C_n \cosh(\lambda_ n z) + D_n \sinh(\lambda_n z )\right) \]
系数求解
由于通解是线性叠加出来的,因此各个子项都应满足边界条件。代入热沉平面的边界条件:
\[ \left.\frac{\partial \theta}{\partial z}\right|_{z=t_{1}}=-\frac{h}{k_{1}}\theta(x,t_1) \]
\[ \begin{aligned} & \lambda_n \left( C_n \sinh(\lambda_ n z) + D_n \cosh(\lambda_n z )\right) = \\ &-\frac{h}{k_{1}} \left( C_n \cosh(\lambda_ n z) + D_n \sinh(\lambda_n z )\right) \end{aligned} \]
于是\(C_n\)和\(D_n\)的关系可以整理为:
\[ D_n = - C_n \phi_n(\lambda_n) \]
其中,
\[ \phi_n(\lambda_n) = \frac{\lambda_{n} \sinh \left(\lambda_{n} t_1\right)+\frac{h}{k_1} \cosh \left(\lambda_{n} t_1\right)}{\lambda_{n} \cosh \left(\lambda_{n} t_1\right)+\frac{h}{k_1} \sinh \left(\lambda_{n} t_1\right)} \]
对于理想热沉,底边界为等温边界条件,\(h\rightarrow +\infty\),此时\(\phi_n(x)\)退化为
\[ \left. \phi_n(\lambda_n) \right|_{h\rightarrow +\infty} = \coth (\lambda_n t_1) \]
最终通解中的系数可以通过对热源平面的边界条件做傅里叶展开得到,先求温度梯度表达式:
\[ \begin{aligned} \frac{\partial \theta}{\partial z} = B_0 + \lambda_n \sum_{n=1}^{\infty} \cos(\lambda_n x) \left( C_n \sinh(\lambda_ n z) + D_n \cosh(\lambda_n z )\right) \end{aligned} \]
于是
\[ \begin{aligned} \frac{\partial \theta}{\partial z}\Big|_{z=0} = B_0 + \lambda_n \sum_{n=1}^{\infty} D_n \cos(\lambda_n x) \end{aligned} \]
边界条件\(f(x)\)为:
\[ f(x) = \left\{ \begin{array}{l} \dfrac{\partial \theta}{\partial z} = -\dfrac{\left(Q / c\right)}{k_{1}}, \quad X_c - \dfrac{c}{2} < x < X_c + \dfrac{c}{2}\\ \dfrac{\partial \theta}{\partial z} = 0, \quad others \end{array} \right. \]
作半幅傅里叶级数展开:
\[ f(x) = a_0 + a_n \cos(\lambda_n x), n=1,2,\ldots \]
系数分别为:
\[ \begin{aligned} a_0 &= \frac{1}{a}\int_0^a f(x)dx \\ a_n &= \frac{2}{a}\int_0^a f(x)\cos(\lambda_n x)dx \end{aligned} \]
对比一下温度梯度的表达式,可以得到:
\[ B_0 = -\frac{Q}{ak_1} \]
\[ D_n = \frac{a_n}{\lambda_n} = - \frac{2\int_{X_c - \frac{c}{2}}^{X_c + \frac{c}{2}} Q\cos(\lambda_n x)dx}{ack_1\lambda_n} = \frac{2Q\left( \sin(\lambda_n(X_c - \frac{c}{2})) - \sin(\lambda_n(X_c + \frac{c}{2})) \right)}{ack_1\lambda_n^2} \]
又有
\[ C_n = - \frac{D_n}{\phi(\lambda_n)} = \frac{2Q\left( \sin(\lambda_n(X_c + \frac{c}{2})) - \sin(\lambda_n(X_c - \frac{c}{2})) \right)}{ack_1\lambda_n^2 \phi(\lambda_n)} \]
线性部分的解为:
\[ A_0 = \frac{Q}{a}\left( \frac{t_1}{k_1} + \frac{1}{h} \right) \]
此时已经解出来所需要的表达式了..
温度与热阻
热源平面的温度表达式为:
\[ \begin{aligned} \theta \Big|_{z=0} &= A_0 + \sum_{n=1}^{\infty} \cos(\lambda_n x) C_n\\ &= \frac{Q}{a}\left( \frac{t_1}{k_1} + \frac{1}{h} \right) + \sum_{n=1}^{\infty} \cos(\lambda_n x)\frac{2Q\left( \sin(\lambda_n(X_c - \frac{c}{2})) - \sin(\lambda_n(X_c + \frac{c}{2})) \right)}{ack_1\lambda_n^2 \phi(\lambda_n)} \end{aligned} \]
热源区域的平均温度为:
\[ \begin{aligned} \bar{\theta}_s &= \frac{1}{c} \int_{X_c + \frac{c}{2}}^{X_c - \frac{c}{2}} A_0 + \sum_{n=1}^{\infty} \cos(\lambda_n x) C_n dx \\ &= \frac{Q}{a}\left( \frac{t_1}{k_1} + \frac{1}{h} \right) + \sum_{n=1}^{\infty} \frac{8 Q \sin ^{2}\left(\frac{c \lambda_n}{2}\right) \cos ^{2}\left(X_{c} \lambda_n\right)}{a c^2 k_{1} \lambda_n^{3} \phi_n(\lambda_n)} \end{aligned} \]
总热阻为
\[ R_t = \frac{\bar{\theta_s}}{Q} = R_{1D} + R_s \]
一维热阻的表达式为
\[ R_{1D} = \frac{1}{a}\left( \frac{t_1}{k_1} + \frac{1}{h} \right) \]
扩展热阻
\[ R_{s} = \sum_{n=1}^{\infty} \frac{8 \sin ^{2}\left(\frac{c \lambda_n}{2}\right) \cos ^{2}\left(X_{c} \lambda_n\right)}{a c^2 k_{1} \lambda_n^{3} \phi_n(\lambda_n)} \]
一个例子
考虑下面这个二维、热源处在顶部中心,底部为等温边界条件的情况
此时总热阻的表达式为:
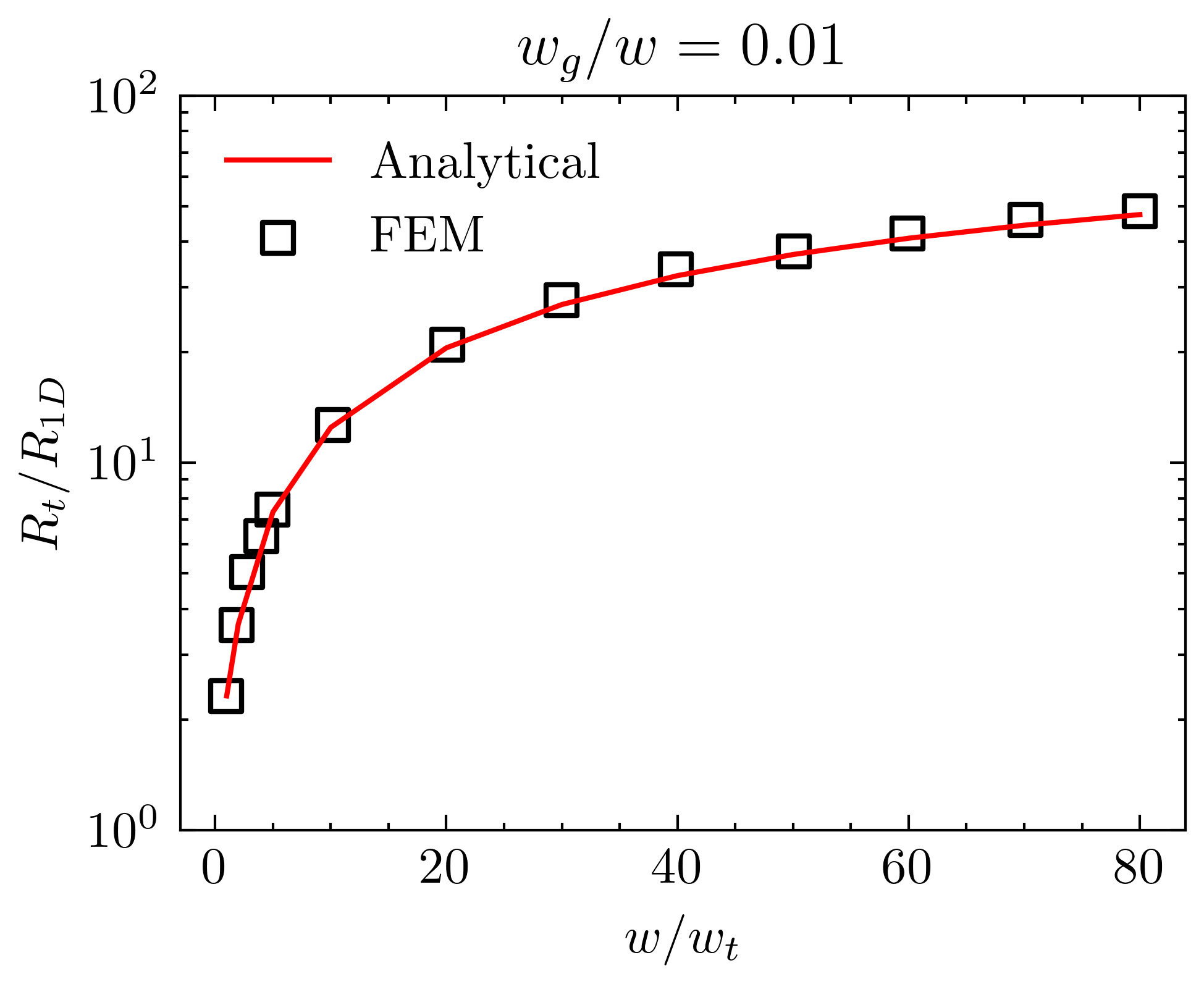
\[ \begin{aligned} R_t / R_{1D} &= 1 + \sum_{n=1}^{\infty} \frac{8 \sin ^{2}\left(\frac{w_g n\pi}{2w}\right)\cos^2(\frac{n\pi}{2})}{w_g^2 t (\frac{n\pi}{w})^{3} \coth(\frac{tn\pi}{w} )} \\ &= 1 + (\frac{w}{w_g})^2(\frac{w}{t})\sum_{n=1}^{\infty} \frac{8 \sin ^{2}\left(\frac{w_g n\pi}{2w}\right) * \cos^2(\frac{n\pi}{2})}{(n\pi)^3 \coth(\frac{tn\pi}{w} )} \end{aligned} \]
1 | import numpy as np |
和有限元结果对比一下,因为它没引入任何近似,所以实际上就是真实解: