输运过程(1)-从BTE到声子热导率

Chen G. Nanoscale energy transport and conversion: a parallel treatment of electrons, molecules, phonons, and photons[M]. Oxford university press, 2005.

线性Boltzmann方程

在弛豫时间近似下，BTE的形式为： \[ \frac{\partial f}{\partial t}+v \cdot \nabla_{r} f+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f=-\frac{f-f_{0}}{\tau} \] 引入偏差函数： \[ g = f - f_0 \] 此时BTE可以改写为： \[ \frac{\partial g}{\partial t}+\frac{\partial f_{0}}{\partial t}+v \cdot \nabla_{r} f_{0}+v \cdot \nabla_{r} g+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} g=-\frac{g}{\tau} \] 考虑分布函数离平衡态偏差很小的情况，此时成立以下假设：

• 非稳态项可以忽略
• \(g\)的梯度远远小于\(f_0\)的梯度
• \(g\)远小于\(f_0\)

于是方程可以简化为： \[ g=-\tau\left(v \cdot \nabla_{r} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}\right) \] 即： \[ f=f_0-\tau\left(v \cdot \nabla_{r} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}\right) \] 在小扰动情况下，分布函数的解可以通过把\(g\)看成是\(f\)的一阶展开（\(f_0\)是\(f\)的零阶展开）并忽略高阶项得到，这个方程被称作线性Boltzmann方程，由分布函数可以计算各种感兴趣物理量的通量，进而计算等效输运系数。

傅立叶定律与声子热导率

考虑声子的热传导，这种情况没有外力，平衡分布为玻色-爱因斯坦分布，这个分布只是温度的函数： \[ f_{0}=\frac{1}{\exp \left(\hbar \omega / k_{\mathrm{B}} T\right)-1} \] 于是线性BTE可以写为： \[ f(\boldsymbol{r}, \boldsymbol{k})=f_{0}-\tau \frac{\mathrm{d} f_{0}}{\mathrm{~d} T} \boldsymbol{v} \cdot \nabla T \] x方向的热通量公式为： \[ J_{q x}(x)=\sum_{s}\left[\frac{1}{V} \sum_{k_{x 1}} \sum_{k_{y 1}} \sum_{k_{z 1}}v_{x} \hbar \omega f\right] \] 其中\(\sum_{s}\)代表对所有声子支求和。要注意\(f(\boldsymbol{r}, \boldsymbol{k})\)是一个六维变量的函数，即使三个空间坐标的函数也是三个波矢空间坐标的函数，因此在计算实空间某一点的物理量时，要考虑波矢空间所有的贡献。在统计物理的图像中，可以理解为存在着一系列不同的能级，每一能级上都分布着不同数目的声子，不同能级上的声子的性质也不相同，宏观的性质是各个能级上的声子贡献之和。在声子图像中，我们认为声子有着不同支，每一支又有着不同波矢的状态，这一个状态叫作一个声子模式，就相当于统计物理中的一个能级，\(f\)就代表这个能级上的声子数目。

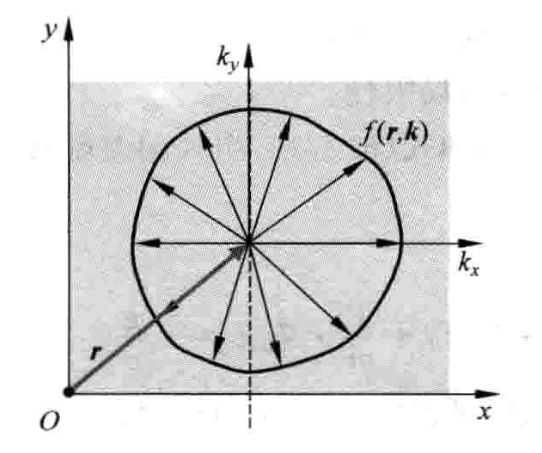
将离散求和改写为积分：

$$ \[\begin{aligned} J_{q x}(x) &=\sum_{s}\left[\frac{1}{V} \sum_{k_{x 1}} \sum_{k_{y 1}} \sum_{k_{z 1}}v_{x} \hbar \omega f\right]\\ &=\sum_{s} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} v_{x} \hbar \omega f \mathrm{~d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} /(2 \pi)^{3} \\ &=\int_{0}^{\omega_{\max }} \mathrm{d} \omega\left[\int_{0}^{2 \pi}\left\{\int_{0}^{\pi} v \cos \theta \hbar \omega f \frac{D(\omega)}{4 \pi} \sin \theta \mathrm{d} \theta\right\} \mathrm{d} \varphi\right] \end{aligned}\]

$$

这里要做一些说明，在量子理论中，在能量准连续的条件下，对于量子数足够大的状态，一个量子态在相空间中对应\(h^r\)的相体积，其中\(r\)为粒子的自由度数目，对于三维的粒子来说，\(r=3\)。于是量子态数目可以表示为：

\[ \begin{aligned} N &= \Omega / h^3 \\ &= \int \mathrm{d}x\mathrm{d}y\mathrm{d}z\mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z / h^3 \\ &= V\int \hbar^3 \mathrm{d} k_x \mathrm{d} k_y \mathrm{d} k_z / h^3\\ &= V/(2\pi)^3 \int \mathrm{d} k_x \mathrm{d} k_y \mathrm{d} k_z \end{aligned} \] 于是\(k\)空间中一个量子态的体积为\((2\pi)^3/V\)，代回到上面热流公式得到第二行的积分表达式。把第二行笛卡尔坐标系积分转化成球坐标系积分： \[ \begin{aligned} & \sum_{s} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} v_{x} \hbar \omega f \mathrm{~d} k_{x} \mathrm{~d} k_{y} \mathrm{~d} k_{z} /(2 \pi)^{3} \\ &=\sum_{s} \int_{0}^{\infty} \mathrm{d}k \int_{0}^{\pi}\mathrm{d}\theta \int_{0}^{2\pi}\mathrm{d} \phi \, k^2\sin\theta v \cos \theta \hbar \omega f / (2 \pi)^{3} \end{aligned} \] 波矢和频率满足： \[ \int_0^{\infty}\mathrm{d}k = \int_0^{\omega_{max}}\frac{\mathrm{d}k}{\mathrm{d}\omega}\mathrm{d}\omega = \int_0^{\omega_{max}}\frac{1}{v}\mathrm{d}\omega \] 于是： \[ \begin{aligned} &\sum_{s} \int_{0}^{\infty} \mathrm{d}k \int_{0}^{\pi}\mathrm{d}\theta \int_{0}^{2\pi}\mathrm{d} \phi \, k^2\sin\theta v \cos \theta \hbar \omega f / (2 \pi)^{3}\\ &=\sum_{s} \int_{0}^{\omega_{\max}} \mathrm{d}\omega \int_{0}^{\pi}\mathrm{d}\theta \int_{0}^{2\pi}\mathrm{d} \phi \, k^2\sin\theta \cos \theta \hbar \omega f / (2 \pi)^{3} \end{aligned} \] 同时，可以把上面量子态数目的表达式写成球坐标的形式： \[ \begin{aligned} N &= V/(2\pi)^3 \int \mathrm{d} k_x \mathrm{d} k_y \mathrm{d} k_z \\ &= V/(2\pi)^3 \int 4\pi k^2 \mathrm{d}k \\ &= V/(2\pi)^3 \int_0^{\omega_{max}} 4\pi k^2 /v \, \mathrm{d}\omega \\ &= V \int_0^{\omega_{max}} \frac{k^2}{2\pi^2 v}d\omega \end{aligned} \] 把\(\dfrac{k^2}{2\pi^2 v}\)定义为态密度\(D(\omega)\)，于是就把量子态沿波矢大小的分布转换到沿频率大小的分布上了，在统计物理中，这个态密度实际上就是能级的简并度。将态密度的表达式代入热流公式的球坐标积分中： \[ J_{q x}(x) = \sum_{s} \int_{0}^{\omega_{\max}} \mathrm{d}\omega \int_{0}^{\pi}\mathrm{d}\theta \int_{0}^{2\pi}\mathrm{d} \phi \,D(\omega)\sin\theta v \cos \theta \hbar \omega f / 4\pi \] 将线性玻尔兹曼方程代入热流公式： \[ \begin{aligned} J_{q x}(x) &=\int_{0}^{\omega_{\max }} \mathrm{d} \omega\left[\int_{0}^{2 \pi}\left\{\int_{0}^{\pi} v \cos \theta \hbar \omega\left[f_{0}-\tau \frac{\mathrm{d} f_{0}}{\mathrm{~d} T} \frac{\mathrm{d} T}{\mathrm{~d} x} v \cos \theta\right] \frac{D(\omega)}{4 \pi} \sin \theta \mathrm{d} \theta\right\} \mathrm{d} \varphi\right] \\ &=-\frac{1}{2} \frac{\mathrm{d} T}{\mathrm{~d} x} \int_{0}^{\omega_{\max }} \mathrm{d} \omega\left\{\int_{0}^{\pi} \tau v^{2} \sin \theta \cos ^{2} \theta \times \hbar \omega D(\omega) \frac{\mathrm{d} f_{0}}{\mathrm{~d} T} \mathrm{~d} \theta\right\} \end{aligned} \] 平衡分布不对通量作出贡献，能量从左到右以及相反传递时，它的值相同。此时热流的表达式可以写成傅里叶定律的形式： \[ J_{q x}(x) = -k \frac{\mathrm{d}T}{\mathrm{d}x} \] 于是热导率的表达式为： \[ k = -\frac{1}{2}\int_{0}^{\omega_{\max }} \mathrm{d} \omega\left\{\int_{0}^{\pi} \tau v^{2} \sin \theta \cos ^{2} \theta \times \hbar \omega D(\omega) \frac{\mathrm{d} f_{0}}{\mathrm{~d} T} \mathrm{~d} \theta\right\} \] 其中， \[ C_{\omega}=\hbar \omega D(\omega) \mathrm{d} f_{0} / \mathrm{d} T \] 是在频率\(\omega\)和温度\(T\)下单位频率的比热，于是： \[ k = \frac{1}{3} \int \tau v^{2} C_{\omega} \mathrm{d} \omega = \frac{1}{3} \int C_{\omega}vl \mathrm{d} \omega \]