输运过程(2)-从BTE到分子粘度

Chen G. Nanoscale energy transport and conversion: a parallel treatment of electrons, molecules, phonons, and photons[M]. Oxford university press, 2005.

线性Boltzmann方程

在弛豫时间近似下，BTE的形式为： \[ \frac{\partial f}{\partial t}+v \cdot \nabla_{r} f+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f=-\frac{f-f_{0}}{\tau} \] 引入偏差函数： \[ g = f - f_0 \] 此时BTE可以改写为： \[ \frac{\partial g}{\partial t}+\frac{\partial f_{0}}{\partial t}+v \cdot \nabla_{r} f_{0}+v \cdot \nabla_{r} g+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} g=-\frac{g}{\tau} \] 考虑分布函数离平衡态偏差很小的情况，此时成立以下假设：

• 非稳态项可以忽略
• \(g\)的梯度远远小于\(f_0\)的梯度
• \(g\)远小于\(f_0\)

于是方程可以简化为： \[ g=-\tau\left(v \cdot \nabla_{r} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}\right) \] 即： \[ f=f_0-\tau\left(v \cdot \nabla_{r} f_{0}+\frac{\boldsymbol{F}}{m} \cdot \nabla_{v} f_{0}\right) \] 在小扰动情况下，分布函数的解可以通过把\(g\)看成是\(f\)的一阶展开（\(f_0\)是\(f\)的零阶展开）并忽略高阶项得到，这个方程被称作线性Boltzmann方程，由分布函数可以计算各种感兴趣物理量的通量，进而计算等效输运系数。

牛顿剪切应力定律

Maxwell速度分布率：

\[ P(p_x,p_y,p_z) = \left(\frac{1}{2 \pi m k T}\right)^{3 / 2} \exp \left[-\frac{p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2 m k T}\right] \]

这个速度分布律实际上是粒子数按能量的分布律，采用玻尔兹曼统计可以很显然地得到这个速度分布，理想气体在温度\(T\)平衡时满足玻尔兹曼分布： \[ n_i = g_ie^{-\alpha - \beta \epsilon_i} \] 其中\(n_i\)是第\(i\)个能级上的粒子数，\(g_i\)是第\(i\)个能级的简并度，\(\beta=1/(kT)\)，\(\epsilon_i\)是第\(i\)个能级的能量，总粒子数可以写成 \[ N = e^{-\alpha}\sum_i g_i e^{-\beta\epsilon_i} = e^{-\alpha}Z \] 把\(Z\)叫作配分函数。这个简并度的意思是一个能量可能对应着多个量子态，比如在能量相等时动量可以分布在一个球面上。但是一个量子态在相空间中的体积永远是\(h^r\)\(r，\)为粒子的自由度，对于三维平动的分子就是3，也就是说从能量的角度考虑，是有简并度的，而从相空间（动量）直接考虑就是没有简并度的，这个时候相空间中的一块体积就代表一个单量子态。因此 \[ \begin{aligned} Z &= \int_0^\infty e^{-\beta\epsilon}g(\epsilon)\mathrm{d}\epsilon\\ &= \frac{1}{h^3}\int e^{-\beta\epsilon}\mathrm{d}x\mathrm{d}y\mathrm{d}z\mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\\ &= \frac{4\pi V}{h^3}\int e^{-\dfrac{p^2}{2mkT}}p^2\mathrm{d}p\\ &= \frac{V}{h^3}\left(2\pi m kT \right)^{3/2} \end{aligned} \] 因此 \[ e^{-\alpha} = \frac{N}{V}h^3 (2\pi mkT)^{-3/2} \] 因此 \[ n_i = g_ie^{-\alpha - \beta \epsilon_i} =\frac{N}{V}h^3 (2\pi mkT)^{-3/2} g_i e^{-\beta \epsilon_i} \] 现在考虑动量空间中的\(g_i\)，在相空间体积元\(\mathrm{d}\Omega\)的单粒子态数目为： \[ \mathrm{d}\Omega/h^3 = \mathrm{d}x\mathrm{d}y\mathrm{d}z\mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z/h^3 \] 因此在动量空间内一个体积元\(\mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\)的粒子态数目为\(V/h^3 \mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\)

于是 \[ n(p_x,p_y,p_z) = N \left(\frac{1}{2 \pi m k T}\right)^{3 / 2} \exp \left[-\frac{p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2 m k T}\right] \]

一维粘性层流

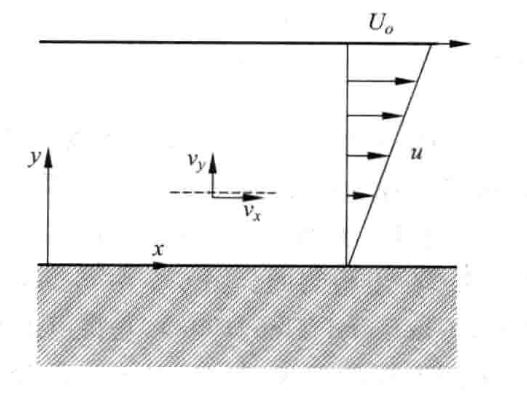
一维粘性层流的速度分布可以认为是平均速度和分子随机运动速度的叠加，因此粒子的速度分布可以认为是麦克斯韦分布的偏移： \[ P(p_x,p_y,p_z) = \left(\frac{1}{2 \pi m k T}\right)^{3 / 2} \exp \left[-\frac{(p_{x} - mu)^{2}+p_{y}^{2}+p_{z}^{2}}{2 m k T}\right] \] 假设粒子数密度为\(n\)，于是具有动量\(\boldsymbol{p}\)的粒子数密度为： \[ f_0 (p_x,p_y,p_z) = n\left(\frac{1}{2 \pi m k T}\right)^{3 / 2} \exp \left[-\frac{(p_{x} - mu)^{2}+p_{y}^{2}+p_{z}^{2}}{2 m k T}\right] \] 于是分布函数为： \[ f = f_0 - \tau v_y\frac{\partial f_0}{\partial y} = f_0 - \tau v_y\frac{\partial f_0}{\partial u}\frac{\partial u}{\partial y} \] 求粘度实际上就是用分布函数写出动量通量的表达式，在垂直于y轴的平面内，沿x方向的剪切应力对应着在单位时间内通过垂直y轴平面的流体分子沿x方向的动量通量，因此 \[ \begin{aligned} \tau_{xy} &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\left[mv_x\right]v_yf \mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\\ &= -\frac{\partial u}{\partial y} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} mv_xv_y \tau v_y\frac{\partial f_0}{\partial u} \mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z \end{aligned} \] 于是 \[ \begin{aligned} \mu &= -\tau/m^2\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} p_xp_y^2 \frac{\partial f_0}{\partial u} \mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\\ \end{aligned} \]

\[ \frac{\partial f_0}{\partial u} = n\left(\frac{1}{2 \pi m k T}\right)^{3 / 2} \exp \left[-\frac{(p_{x} - mu)^{2}}{2 m k T}\right] \exp \left[\frac{p_{y}^{2}}{2mkT}\right] \exp \left[\frac{p_{z}^{2}}{2mkT}\right]\frac{p_x - mu}{kT} \]

于是 \[ \begin{aligned} \mu &= -\tau/m^2\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} p_xp_y^2 \frac{\partial f_0}{\partial u} \mathrm{d}p_x\mathrm{d}p_y\mathrm{d}p_z\\ &= \tau n / m^2 \left(\frac{1}{2 \pi m k T}\right)^{3 / 2}\int_{-\infty}^\infty p_x(\frac{p_x - mu}{kT})\exp \left[-\frac{(p_{x} - mu)^{2}}{2 m k T}\right] \mathrm{d}p_x\\ &\times \int_{-\infty}^\infty \exp \left[\frac{p_{y}^{2}}{2mkT}\right]p_y^2 \mathrm{d}p_y \int_{-\infty}^\infty \exp \left[\frac{p_{z}^{2}}{2mkT}\right] \mathrm{d}p_z\\ & = n\tau k T \end{aligned} \] 通过麦克斯韦速度分布及平均自由程表达式，可以得到粘度的最终表达式为： \[ \mu = \frac{1}{4 d^{2}} \sqrt{\frac{m \kappa_{\mathrm{B}} T}{\pi}} \]