刘维尔定理
刘维尔定理与不可压流体
刘维尔定理
密度函数\(\rho(\boldsymbol{q},\boldsymbol{p},t)\) : 在任意时刻\(t\), 在相空间内点\((\boldsymbol{q},\boldsymbol{p})\)周围的体积元\(d^{3N}qd^{3N}p\)中,代表点的数目由乘积\(\rho(q,p,t)d^{3N}\boldsymbol{q}d^{3N}\boldsymbol{p}\)确定. 也就是说,密度函数是相点分布的一种描述方式. 其中\(\boldsymbol{q},\boldsymbol{p}\)分别是广义坐标和广义动量,其在相空间中的运动满足哈密顿方程:
\[ \dot{\boldsymbol{q}} = \frac{\partial H}{\partial \boldsymbol{p}} \\ \dot{\boldsymbol{p}} = -\frac{\partial H}{\partial \boldsymbol{q}} \] 相空间中的代表点运动,就相当于流体在物理空间中运动,只不过相点是\((q,p,t)\)的函数,而流体是\((q,t)\)的函数. 同样,可以定义相空间中的速度: \[ v = \frac{d(\boldsymbol{q},\boldsymbol{p})}{dt} = (\frac{dq_1}{dt},\ldots,\frac{dq_{3N}}{dt},\frac{dp_1}{dt},\ldots,\frac{dp_{3N}}{dt}) \] 用上方的哈密顿方程代换,则有: \[ v = \frac{d(q,\boldsymbol{p})}{dt} =(\frac{\partial H}{\partial p_1},\ldots,\frac{\partial H}{\partial p_{3N}},-\frac{\partial H}{\partial q_1},\ldots,-\frac{\partial H}{\partial q_{3N}}) \] 自然,相空间中的速度同样可以定义散度: \[ div(v) = \sum_{i=1}^{3N}\left[\partial(\frac{dq_i}{dt})/\partial q_i + \partial(\frac{dp_i}{dt})/\partial p_i\right] = \sum_{i=1}^{3N}(\frac{\partial^2H}{\partial p_i\partial q_i}-\frac{\partial^2H}{\partial q_i\partial p_i}) = 0 \] 相空间速度的散度为0,实际上对应了物理空间中的不可压缩流体的运动,考察密度函数的连续性方程: \[ \frac{\partial \rho}{\partial t}+\sum_{i=1}^{d}\left(\frac{\partial\left(\rho \dot{q}^{i}\right)}{\partial q^{i}}+\frac{\partial\left(\rho \dot{p}_{i}\right)}{\partial p_{i}}\right)=0 \] 可以将对流项展开: \[ \sum_{i=1}^{3N}\left(\frac{\partial\left(\rho \dot{q}^{i}\right)}{\partial q^{i}}+\frac{\partial\left(\rho \dot{p}_{i}\right)}{\partial p_{i}}\right) = \sum_{i=1}^{3N}\left( \rho div(\boldsymbol{v}) + \frac{\partial \rho}{\partial q^{i}} \dot{q}^{i}+\frac{\partial \rho}{\partial p_{i}} \dot{p}_{i}\right) = \sum_{i=1}^{3N}\left(\frac{\partial \rho}{\partial q^{i}} \dot{q}^{i}+\frac{\partial \rho}{\partial p_{i}} \dot{p}_{i}\right) \] 于是连续性方程可变为:
\[ \frac{d \rho(\boldsymbol{q},\boldsymbol{p},t)}{d t}=\frac{\partial \rho}{\partial t}+\sum_{i=1}^{3N}\left(\frac{\partial \rho}{\partial q^{i}} \dot{q}^{i}+\frac{\partial \rho}{\partial p_{i}} \dot{p}_{i}\right)=0 \] 这说明\(\rho(\boldsymbol{q},\boldsymbol{p},t)\)的随体导数为0,即刘维尔定理:相空间的分布函数沿着系统的轨迹是常数——即给定一个系统点,在相空间游历过程中,该点邻近的系统点的密度关于时间是常数. 在体系达到平衡时: \[ \frac{\partial \rho}{\partial t} = 0 \] 即: \[ \sum_{i=1}^{3N}\left(\frac{\partial \rho}{\partial q^{i}} \dot{q}^{i}+\frac{\partial \rho}{\partial p_{i}} \dot{p}_{i}\right)=0 \] 满足这个分布的密度函数应该是什么样的呢?可以假设\(\rho\)就是哈密顿函数\(H(q,p)\)的泛函: \[ \rho(\boldsymbol{q},\boldsymbol{p}) = \rho[H(\boldsymbol{q},\boldsymbol{p})] \] 哈密顿量为常数,自然满足上面的方程.
实际上正则系综的密度函数就是: \[ \rho(\boldsymbol{q},\boldsymbol{p}) \propto \exp\left[ -\frac{H(\boldsymbol{q},\boldsymbol{p})}{kT} \right] \]
不可压缩流体
体积守恒
刘维尔定理说明了相点在相空间中的运动是不可压缩流体的运动,也就是说明相空间中的体积是守恒的,这反映了相空间的不可压缩性. 对应一大块不可压缩流体,流体在运动的过程中形状可能发生改变,但是流体的总体积保持不变. 追随一个相点,其密度在演化过程中保持不变. 这是拉格朗日描述.
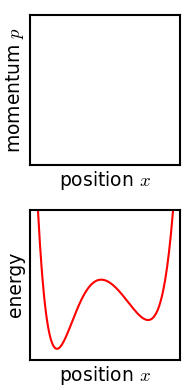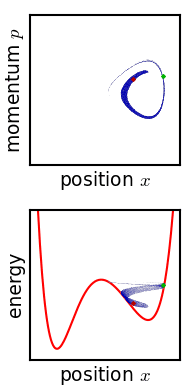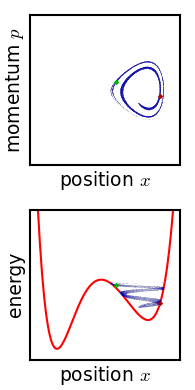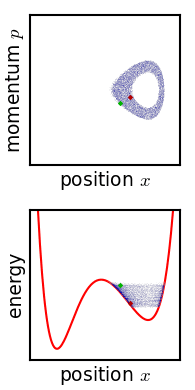
分布函数
不可压缩流体不代表这个密度函数就是均匀分布的,不可压缩的水和油掺混后整体还是不可压缩的. 混合液体在流动中形状可能发生改变,但是流体的总体积保持不变,这和用刘维尔定理描述相空间的不可压缩性是一样的. 追随一个无限小的油或者一个无限小的水滴观察,会发现他们在运动中的密度都是保持不变的. 将油和水扩展为无数种密度不同的小液滴掺混而成的混合流体,会发现流体中的每一点的密度都是不一样的,也就因此可以用一个分布函数来描述这种分布,但整体还是不可压缩的.
所以这也就解释了即使相空间是不可压缩的,但是仍然可以存在一个密度分布: \[ \rho(\boldsymbol{q},\boldsymbol{p}) \propto \exp\left[ -\frac{H(\boldsymbol{q},\boldsymbol{p})}{kT} \right] \] 对于正则分布的密度函数,也就可以理解为只要选定了一个相点\((\boldsymbol{q},\boldsymbol{p})\)观察它的演化,它的密度函数就是保持不变的.
总结
相空间不可压缩 ------ 流体不可压缩
相空间在演化过程中总体积保持不变 ------ 不可压缩流体总体积保持不变
相空间的密度分布函数在全空间积分为1 ------ 流体总质量不变
相空间存在密度分布函数 ------ 由多种不可压缩流体混合成的混合物存在密度分布