射频系统入门：信息和能量

[TOC]

引言：一场跨越空间的二重奏

通信的根本挑战，千百年来从未改变：如何将信息从一个点，有效传递到另一个点。

但这背后隐藏着一个更深的物理现实：信息本身是抽象的，要让它旅行，就必须将其“附着”在一个物理载体上；而驱动这个载体跨越空间，则必须消耗能量。

在古代，一封信（信息载体）的传递，依靠的是马匹或信鸽消耗的生物代谢能。信息与能量，被捆绑在同一个物理实体上。现代的有线网络，如办公室的局域网，原理也异曲同工：信息被编码成电脉冲，而驱动这些脉冲的能量则由电网供给，两者都被牢牢地约束在实体线缆之中。

然而，当物理的连接不复存在时——对于天空中的飞行员、口袋里的智能手机、或是荒野中的探险家——挑战便升级为一场关于信息与能量的二重奏：

1. 信息的挑战： 我们该如何将复杂的信息（语音、图像、数据）打包，赋予它一种能够在开放空间中自由穿行的形态？
2. 能量的挑战： 我们又该如何为这个“信息包裹”注入足够强大的能量，让它能够克服距离、障碍和干扰，精准地抵达目的地？

这便是无线通信的本质。而物理学为我们提供的完美答案，就是电磁波。

电磁波，是物理世界的一项杰作。它既是承载信息的精妙载体，又是投射能量的有力炮弹。

这双重属性，定义了整个射频工程领域，也是我们这趟探索之旅的核心主题。在这篇博客中，我们将一同探寻这两个根本问题的答案：

• 关于信息： 我们如何巧妙地操控电磁波的属性——它的幅度、频率和相位——来“雕刻”出我们想传递的消息？这将带领我们进入调制与带宽的世界。
• 关于能量： 我们如何从电池或插座中获取原始的电能，将其转换为高频信号，并用千百倍的力量将其放大，最终成功地发射到空中？这将带领我们深入功率放大器、效率与阻抗匹配的核心。

那么，就让我们从这个神奇的“信使”——电磁波本身开始，去揭示它如何同时服务于信息与能量这两位“主人”的吧。

电磁波

基本概念

根据经典的电磁学理论，电磁波是由同相振荡且相互垂直的电场和磁场在空间中以波的形式传播的能量和动量。变化的电场会激发出磁场，而变化的磁场又会反过来产生电场。这个过程如同一个永动机，电场和磁场相互激励、交替产生，形成一个自我传播的整体。这个电磁场组合以光速向外传播，并且其传播方向同时垂直于电场和磁场的振动方向。 在著名的麦克斯韦方程组中，电磁波本质上就是一个随时间震荡的电场和磁场的解：

\[ E(t)\sim\sin(\omega t), B(t)\sim\sin(\omega t) \] 要发射和接收电磁波，我们需要一个关键器件——天线。天线是无线通信系统不可或缺的组成部分，它负责将电信号转换成电磁波辐射出去，或者将空间中的电磁波捕获并转换回电信号。

最简单也最基础的天线形式之一是偶极子天线 (Dipole antenna)。它通常由两根对称放置的导体制成。

• 发射过程：当我们将一个高频交流电压施加到偶极子天线的两个导体臂上时，导体上的电子会随着电压的交替变化而来回振荡。 这种电子的加速运动会在天线周围产生一个迅速变化的电场。根据电磁感应定律，这个变化的电场会继而产生一个变化的磁场。这个新生的、变化的磁场又会再次激发出新的电场，如此循环往复，形成一个相互垂直、不断向外传播的电磁波。

• 接收过程：当传播中的电磁波遇到一个接收天线时，其变化的电场会对天线导体内的电子施加一个力，导致电子在导体中产生振荡，从而在天线两端感应出微弱的交流电压。这个电压的频率与原始发射的电磁波频率完全相同，因此它承载了原始信号的信息。接收设备将这个微弱的信号放大并进行解调，就可以还原出发射端想要传递的信息了。

电磁波特性和波段

在探索一个新领域时，我们有时需要暂时接受一些基本概念作为“公理”，以此为基础来理解更复杂的现象。对于射频通信应用而言，我们可以先将电磁波直观地理解为一个以光速传播、携带能量、以某种频率震荡的“波”，它最核心的两个属性是频率和波长。

电磁波的频率 (\(f\)) 指的是其电场和磁场每秒钟振荡的次数，单位是赫兹 (Hz)。而波长 (\(\lambda\)) 则是指在传播方向上，相邻两个波峰或波谷之间的距离。这两者通过光速 (\(c\)) 紧密相连： \[ c = \lambda f \] 这个简单的关系式意味着，频率越高，波长就越短，反之亦然。电磁波的频率（或波长）直接决定了它的诸多关键物理特性，从而也决定了它在不同领域的应用。我们暂时不去细究频率和波长到底是以什么机理影响电磁波的特性的，只是先接受习惯这些关系。

1. 能量大小

根据普朗克-爱因斯坦关系式，单个光子的能量 (\(E\)) 与其频率成正比： \[ E = h f \] 其中 \(h\) 是普朗克常数。这意味着频率越高的电磁波，其携带的能量就越强。例如，高能量的紫外线、X射线和伽马射线能够破坏分子化学键，甚至引发DNA突变。相比之下，无线电波和微波等低频电磁波的能量则非常低，不足以改变物质的分子结构，其主要效应是引起分子振动或产生热效应。

2. 穿透与绕射能力

电磁波与障碍物的相互作用方式也与波长密切相关。

• 绕射：频率较低、波长较长的电磁波具有更强的绕射能力，这意味着它们可以更好地“绕过”建筑物、山丘等大型障碍物，实现超视距传播。
• 穿透：频率更高、波长更短的电磁波（如X射线）则表现出更强的穿透性。这主要是因为它们的波长远小于原子间距，能量也足够高，可以像微小粒子一样直接穿过物质的原子间隙。然而，这种穿透性并非绝对的，它们仍然会被密度较高的物质（如骨骼对X射线的阻挡）所吸收或散射。

3. 大气传播特性

大气层对不同频率的电磁波会产生不同的影响，主要是吸收和散射。

• 散射：大气中的分子会对电磁波产生散射效应，并且这种散射的强度与频率的四次方成正比（瑞利散射）。这就是为什么天空呈现蓝色，因为波长较短的蓝光比波长较长的红光更容易被大气散射。
• 吸收：大气中的水蒸气和氧气等特定分子会对某些频率的电磁波产生强烈的吸收，形成所谓的“吸收窗口”和“衰减峰”。例如，某些毫米波频段就会受到雨水的严重衰减，这种现象被称为“雨衰”。
• 电离层反射：地球上空的电离层像一面镜子，可以反射特定频段的无线电波（主要是短波），使其能够沿着地球表面传播非常远的距离，实现全球通信。而频率更高的微波和毫米波则会直接穿透电离层，适用于卫星通信和地面点对点通信。

在无线通信领域，我们主要利用的是频率范围在 3 kHz 到 300 GHz 之间的无线电波和微波。在这个广阔的频谱范围内，为了便于管理和应用，人们又将其划分成不同的波段 (Band)。每个波段都因其独特的传播特性而被应用于不同的场景。

上图清晰地展示了卫星通信中常用的几个微波波段及其关键特性：

波段	频率范围 (约)	带宽	天线尺寸	大气衰减 (雨衰)	主要应用
L 波段	1-2 GHz	较小	较大	非常小	GPS、移动卫星电话、海事卫星通信
S 波段	2-4 GHz	较小	较大	小	天气雷达、地面移动通信、部分卫星通信
C 波段	4-8 GHz	中等	中等	较小	早期卫星电视广播、VSAT（甚小孔径终端）
X 波段	8-12 GHz	中等	中等	中等	军事通信、雷达、深空探测
Ku 波段	12-18 GHz	较大	较小	中等	主流卫星电视直播 (DBS)、数据通信
K 波段	18-27 GHz	大	小	较大	(受水蒸气吸收严重，较少直接使用)
Ka 波段	27-40 GHz	非常大	非常小	大	高通量卫星宽带、5G通信、高速数据链

从上表和图中我们可以总结出几个关键规律：

• 频率越高，可用带宽越大：更高的频率意味着可以在单位时间内传输更多的数据，这对于高清视频、高速互联网等大容量业务至关重要。
• 频率越高，天线尺寸越小：天线的物理尺寸通常与波长成正比。频率越高，波长越短，因此可以制造出更小、更便携的接收和发射设备。
• 频率越高，大气衰减越严重：高频信号更容易受到雨、雪、雾等天气现象的影响，信号衰减更严重，通信的可靠性会面临更大挑战。

因此，在设计一个无线通信系统时，工程师必须在带宽、设备尺寸和链路可靠性之间做出权衡，选择最适合应用场景的频段。

信息调制：让电磁波开口说话

概述

我们已经了解，为了实现远距离无线通信，需要通过天线发射特定频率的电磁波。这个用于承载信息的、特定频率的电磁波，我们称之为载波 (Carrier Wave)。

一个关键问题是：为什么需要载波？我们不能直接把声音或数据信号变成电磁波发射出去吗？

原因主要有两点：

1. 天线效率：天线的物理尺寸与它能高效收发的电磁波波长成正比。我们日常通信的音频信号频率很低（例如几百到几千赫兹），对应的波长长达几十甚至上百公里，制造相应尺寸的天线是不现实的。而使用高频载波（如MHz或GHz级别），波长缩短到米、厘米甚至毫米级，天线就可以做得非常小巧。
2. 传播特性：高频信号具有更好的空间传播特性，能够穿透电离层进行卫星通信，或者在地面进行更稳定的视距通信。

因此，我们必须将低频的信息信号 (Message Signal)“附加”到高频的载波上。这个将信息加载到载波上的过程，就叫做调制 (Modulation)。

调制本质上是用信息信号去改变载波的某个参数。当这个携带了信息的载波信号从天线发射出去，被接收方天线接收后，再通过一个逆向的过程——解调 (Demodulation)，将载波信号剥离，就能还原出原始的信息信号。这个过程好比将一封信（信息）装进一个信封并由邮车（载波）运送，到达目的地后再拆开信封取出信。如果邮车在路上被弄脏或损坏（信号受到干扰），我们可能就无法清晰地读出信的内容了。

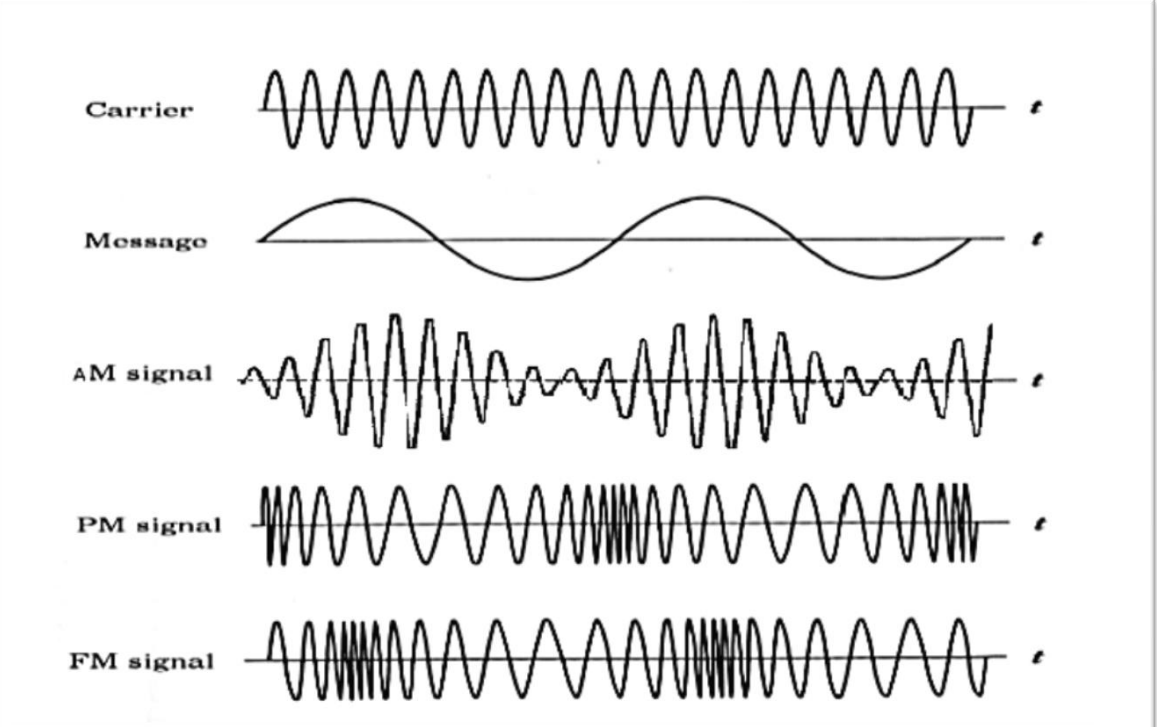
所有的调制方式，万变不离其宗，都是在改变载波信号的三个基本属性之一：幅度 (Amplitude)、频率 (Frequency) 或 相位 (Phase)。

调制方式

幅度调制 (Amplitude Modulation, AM)

这是最经典、最直观的调制方式。AM 的核心思想是：保持载波的频率和相位不变，用信息信号的强弱去控制载波的幅度。

• 什么是幅度？ 信号的幅度可以直观理解为波形的高度。在物理层面，它对应着电磁波电场或磁场强度的峰值。更高的幅度意味着更强的信号能量。
• AM 的优缺点：AM 最大的优点是实现起来非常简单，解调器电路也很容易搭建，这使其成为最早被广泛应用的无线电广播技术。然而，它的致命缺点是抗干扰能力差。自然界和工业环境中的很多噪声源（如雷电、电机火花）产生的干扰，都会表现为信号幅度的突变。AM 接收机无法区分这种突变的幅度变化是来自原始信号还是来自噪声，因此很容易受到干扰，导致收听时背景中常有“嘶嘶”的杂音。

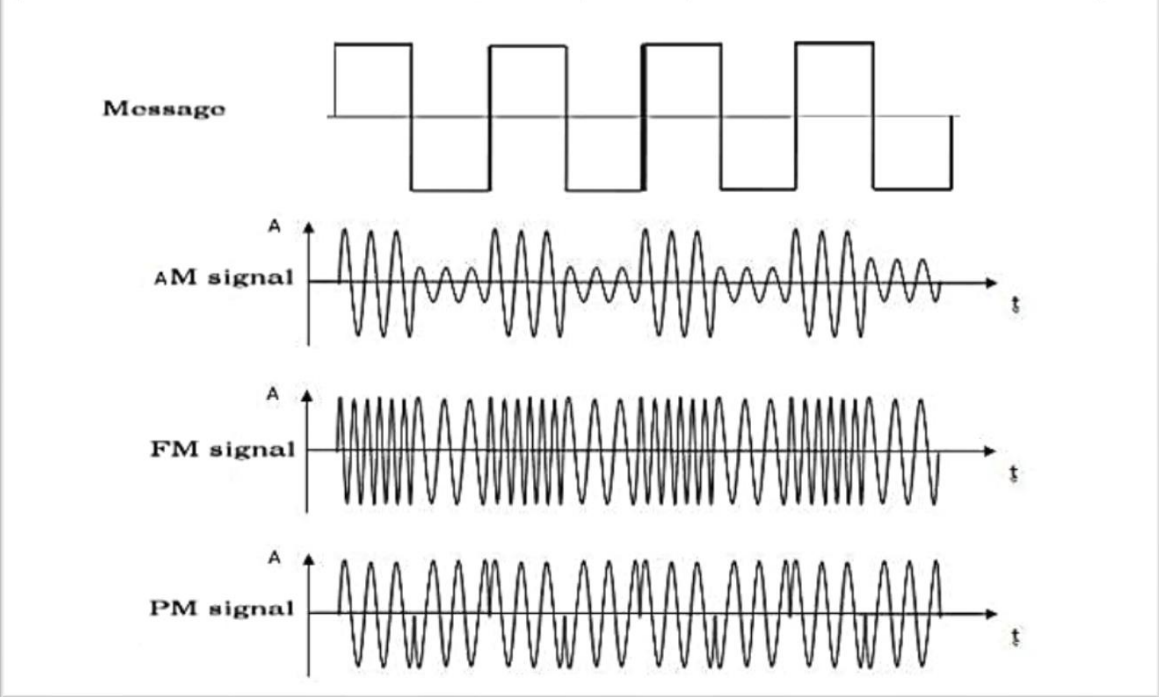
数字版AM：幅移键控 (ASK)

当我们要传输数字信号（0和1）时，可以使用 AM 的数字版本——幅移键控 (Amplitude-Shift Keying, ASK)。最简单的 ASK（也称On-Off Keying, OOK）就是用一个较高的幅度代表“1”，用零幅度（即不发射信号）代表“0”。相比模拟 AM，ASK 对噪声的抵抗力稍强，因为接收端只需要判断信号是“有”还是“无”，而不太关心幅度的微小变化。

---

频率调制 (Frequency Modulation, FM)

为了克服 AM 的噪声问题，人们发明了 FM。FM 的原理是：保持载波的幅度和相位不变，用信息信号的强弱去控制载波的频率。

• 频率变化范围：这是一个非常关键的问题。FM 调制并不会导致载波频率发生巨大的跳变，比如从一个波段跳到另一个波段。实际上，频率的变化非常微小，是围绕着中心载波频率在一个极窄的范围内波动。例如，一个中心频率为 98.1 MHz 的FM广播电台，其频率可能会在 98.025 MHz 到 98.175 MHz 之间变化。这个变化范围远小于该频段的信道宽度，因此它始终工作在指定的“98.1 MHz”信道内，不会干扰其他电台。
• FM的优势：由于信息被编码在频率的变化中，而大多数噪声表现为幅度的变化，因此 FM 接收机可以通过一个“限幅器”电路削平信号顶部，忽略幅度上的干扰，从而获得远比 AM 清晰的音质。

数字版FM：频移键控 (FSK)

与ASK类似，频移键控 (Frequency-Shift Keying, FSK) 是 FM 的数字形式。它使用一个频率（例如 \(f_1\)）来代表“1”，用另一个稍有不同的频率（\(f_2\)）来代表“0”。FSK 的抗干扰能力比 ASK 更强。

延伸知识：为什么收音机要区分AM和FM？

1. 技术不同：AM 和 FM 是两种完全不同的调制解调技术，需要不同的电子线路来处理。
2. 频段不同：根据国际电信联盟 (ITU) 的规定，AM 广播和 FM 广播被分配在完全不同的频率范围。AM广播通常在中波 (MW) 频段（530 kHz - 1700 kHz），而 FM 广播则在甚高频 (VHF) 频段（88 MHz - 108 MHz）。
3. 特性不同：中波 AM 信号波长较长，夜晚可以被电离层反射，实现超远距离传播（能听到几百公里外的电台）。而 VHF 频段的 FM 信号基本是直线传播，覆盖范围较小，但能提供更高的音质（立体声）。

因此，收音机必须内置两套独立的接收和解调系统，并通过一个开关来选择接收 AM 还是 FM 信号。

---

相位调制 (Phase Modulation, PM) 与 相移键控 (Phase-Shift Keying, PSK)

相位调制在现代数字通信中占据着至关重要的地位。其核心思想是：保持载波的幅度和频率不变，用信息信号去改变载波的相位。

正弦波的相位描述了波形在其周期中的起始位置，范围通常是0到360度（或0到2π弧度）。例如，180度的相移意味着波形正好与原始波形上下颠倒。

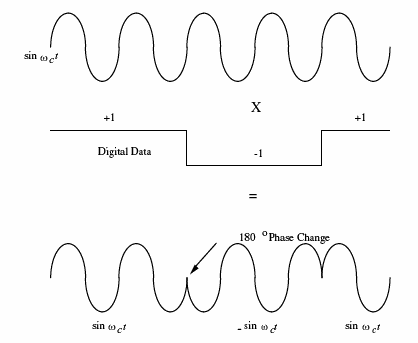
在数字通信中，我们几乎总是使用其数字版本——相移键控 (PSK)。

• BPSK (Binary PSK)：这是最简单的 PSK。它使用两个相反的相位来表示二进制的0和1。例如，用0度相位表示“1”，用180度相位表示“0”。当数据从1跳变为0时，载波的相位会瞬间“翻转”180度。BPSK 非常坚固，抗干扰能力强，但每个符号只能传输1比特信息，效率较低。
• QPSK (Quadrature PSK)：为了提高效率，我们可以使用更多的相位点。QPSK 使用4个相位点（通常是0°, 90°, 180°, 270°）。由于有4个不同的状态，每个相位状态就可以代表2个比特的信息（例如，0° → 00, 90° → 01, 180° → 11, 270° → 10）。这样，在不增加带宽的情况下，QPSK 的数据传输速率是BPSK的两倍。
• 更高阶的PSK：同理，我们还有8-PSK（每个符号传输3比特）、16-PSK（每个符号传输4比特）等。但随着相位点越来越多，它们之间的间隔也越来越小，对噪声就越敏感，更容易出错。

---

高级混合调制：正交幅度调制 (QAM)

如何能进一步提升数据传输速率？一个自然的想法是：将幅移键控 (ASK) 和相移键控 (PSK) 结合起来。这就是正交幅度调制 (Quadrature Amplitude Modulation, QAM) 的核心思想。

QAM同时利用幅度和相位来编码信息。信号的每一个状态都由一个独特的幅度和相位的组合来定义。

这张图生动地解释了 QAM 的效率。我们来解读一下：

• 波特率 (Baud Rate)：也叫符号率，指的是调制信号每秒钟变化的次数。在图中，1秒内信号变化了8次，所以波特率是8 Baud。
• 比特率 (Bit Rate)：指的是每秒钟实际传输的二进制比特数。
• QAM 的威力：在这个例子中（这是一种 8-QAM），每一个符号（baud）都代表了3个比特的信息（例如，某个特定的幅度和相位组合代表"101"）。因此，尽管符号率只有 8 Baud，但实际的数据比特率达到了 8 * 3 = 24 bps (bits per second)。

现代通信系统，如 4G LTE、5G、Wi-Fi 6 等，广泛使用更高阶的 QAM，如 64-QAM（每个符号6比特）、256-QAM（每个符号8比特）甚至 1024-QAM（每个符号10比特），从而在有限的频谱带宽内实现了惊人的数据传输速率。当然，阶数越高的 QAM，对信号质量的要求也越苛刻。

带宽（Bandwidth）

频域和谐波：解锁带宽的钥匙

理解了频率和调制后，我们就可以深入认识带宽的概念了。在射频世界中，带宽指的是一个信号所占据的频率范围的宽度，即其最高频率与最低频率之差。

这是一个至关重要的概念，因为带宽直接与系统的数据承载能力（数据速率）相关联。一个基本法则是：无线系统的带宽越宽，在单位时间内能承载的数据量就越多，数据传输速率也越高。

然而，这个定义初听之下可能会带来一些困惑：

• 在 AM 调制中，我们只是改变载波的振幅，并没有直接去“改变”它的频率，这听起来带宽似乎应该是零？
• 直觉上，似乎应该是载波的频率越高，数据速率才越高？

要解开这些困惑，我们必须引入一个全新的视角——“频域”（Frequency Domain）。我们平时看到的信号随时间变化的波形图，是时域视角。而频域视角则告诉我们，任何复杂的信号，究竟是由哪些频率的纯净正弦波叠加而成的。

这个从时域转换到频域的数学工具就是傅里叶分析。其核心思想是，任何周期性的信号，无论其形状多么奇特，都可以被精确地分解为一系列纯净正弦波（谐波）的线性叠加。

上面这张图诠释了傅里叶分析：一个看似简单的方波（蓝色），实际上是由一个基频正弦波（红色）和一系列频率是基频整数倍的高次谐波（紫色、浅蓝色等）叠加而成的。叠加的谐波越多，合成的波形就越接近完美的方波。

这个理论是理解带宽的基石：调制这个行为本身，就会创造出新的频率成分。

最简单的例子：一次数学证明

为了最清晰地展示这个过程，我们将使用最简单的信号作为原料，通过数学推导来“亲眼”看到新频率的诞生。

第一步：定义我们的“原料”

1. 载波信号 (Carrier Signal), c(t)

   这是一个高频、恒定振幅的纯净波。

\[ c(t) = A_c \cos(2\pi f_c t) \]

​ \(A_c\) 是载波的振幅, \(f_c\) 是载波的频率 (例如 1 MHz)。

2. 信息信号 (Message Signal), m(t)

   我们假设要传递的信息是一个单一频率的纯净“哔”声。

\[ m(t) = A_m \cos(2\pi f_m t) \]

​ \(A_m\) 是信息信号的振幅, \(f_m\) 是信息信号的频率 (例如 1 kHz)。

第二步：进行幅度调制 (AM)

标准的AM调制，就是让载波的整体振幅随着信息信号的瞬时值而变化。因此，调制后总信号 \(s(t)\) 的表达式为： \[ s(t) = [A_c + A_m \cos(2\pi f_m t)] \cdot \cos(2\pi f_c t) \]

第三步：展开表达式（见证新频率的诞生）

利用三角恒等式 \(\cos(A) \cos(B) = \frac{1}{2}[\cos(A-B) + \cos(A+B)]\)，我们将上式展开，得到调制后信号的最终构成： \[ s(t) = \underbrace{A_c \cos(2\pi f_c t)}_{\text{载波}} + \underbrace{\frac{A_m}{2} \cos(2\pi (f_c - f_m) t)}_{\text{下边带 (LSB)}} + \underbrace{\frac{A_m}{2} \cos(2\pi (f_c + f_m) t)}_{\text{上边带 (USB)}} \]

这个公式就是答案，它告诉我们：调制后的信号，虽然在时域上看只是一个振幅变化的波，但在频域上，它不再是单一频率的信号了。它现在是三个不同频率的纯净正弦波的叠加：

1. 原始载波频率: \(f_c\)
2. 下边带频率 (LSB): \(f_c - f_m\)
3. 上边带频率 (USB): \(f_c + f_m\)

第四步：计算带宽

带宽被定义为信号占据的频率范围，即最高频率减去最低频率。 \[ \text{带宽} = (f_c + f_m) - (f_c - f_m) = 2f_m \]

关键结论

带宽由信息决定，与载波无关

所以我们可以理解带宽是如何出现的了。调制行为（在时域是乘法）在频域中必然会导致频率的加和与相减，从而创造出新的频率成分（边带）。带宽不是一个附加品或副作用，它是信息调制这一物理过程内禀的、根本的数学结果。

从对 AM 调制的分析可以看到，最终的带宽公式是 带宽 = \(2f_m\)。我们会发现一个事实：载波频率 \(f_c\) 在最终结果中被完全消掉了。这意味着，一个 AM 信号的带宽只取决于信息信号 \(m(t)\) 本身的频率，而与承载它的载波频率 \(f_c\) 是高是低完全无关。

当然，现实中的音乐或语音信号，并不是一个单一频率的纯音，而是由许多不同频率的正弦波组成的复杂信号（例如，从20Hz到15kHz）。当这个复杂的信号去调制载波时，其中每一个频率成分都会产生自己的一对上下边带。最终，整个调制信号的带宽将由信息信号中最高频率的那个成分来决定。

• 例子：假设我们要广播一段最高频率为15kHz的音乐。
  • 音乐中的100Hz成分会产生 \(f_c \pm 100\text{Hz}\) 的边带。
  • 音乐中的5000Hz成分会产生 \(f_c \pm 5000\text{Hz}\) 的边带。
  • 音乐中的最高频15000Hz成分会产生 \(f_c \pm 15000\text{Hz}\) 的边带。
  • 整个信号的频谱范围从 \(f_c - 15000\text{Hz}\) 延展到 \(f_c + 15000\text{Hz}\)。
  • 总带宽 = \((f_c + 15000) - (f_c - 15000) = 30000\text{Hz} = 30\text{kHz}\)。

这再次证明，带宽是由信息信号的复杂度（最高频率）决定的。信息变化得越快、越复杂（包含的频率成分越高），就需要越宽的带宽来承载。

调和理论与现实的矛盾

上面的 AM 数学推导给了我们一个看似确凿的结论：带宽只由信息信号决定，载波只是搬运工。然而，我们在前面的“电磁波波段”部分又学到：频率越高的波段（如 Ka 波段），其可用带宽越大。

这两个结论看起来是矛盾的：载波频率到底影不影响带宽？

答案是：数学推导和工程现实都在讲述真理，只是角度不同。我们需要区分“信号需要的带宽”和“信道能提供的带宽”。

我们在推导中看到的 \(BW = 2f_m\) 是不可动摇的数学真理。它告诉我们：对于一个特定的信息信号，无论把它搬移到哪个载波频率上，它自身所“必需”占据的频谱宽度是不变的。如果有一个带宽为 10 kHz 的语音信号，无论你用 1 MHz 的中波载波发射它，还是用 30 GHz 的 Ka 波段载波发射它，这个信号本身在频谱上始终只占 10 kHz 的宽度。仅仅提高载波频率，并不会自动让同一个信号传输更多的数据。

既然如此，为什么 5G、卫星通信都要拼命往高频走呢？这就涉及到“可用频谱资源”的问题。让我们用房地产来做一个比喻：

• 电磁频谱 = 土地资源。
• 载波频率 (\(f_c\)) = 土地的地理位置（比如低频是拥挤的市中心，高频是广阔的郊区）。
• 带宽 (BW) = 一块地皮的面积。
• 数据速率 = 在这块地皮上能盖多大的楼（地皮越大，楼能盖得越大）。

现在我们来看不同的频段：

• 低频段（“市中心”）：比如几百 kHz 到几百 MHz 的区域。这里开发得最早，挤满了 AM/FM 广播、电视、对讲机等各种业务。这里的“空地”非常稀缺且狭窄。我们只能申请到很窄的带宽（例如 10 kHz 或 200 kHz）。虽然我们想盖大楼（高数据率），但这里只能提供盖小房子的地皮。
• 高频段（“大郊区/荒漠”）：比如几十 GHz 的毫米波或 Ka 波段。这里以前技术达不到，尚未被大规模开发。这里有连绵不断的、巨大的空闲频谱。在这里，可以轻松划分出 几百 MHz 甚至几 GHz 宽 的连续频带（巨大的地皮）。

所以结论就是，高载波频率本身不创造带宽，但它允许我们使用极宽的带宽，而不会干扰别人：我们想传输超高速数据（如高清视频流）。所以我们的信息信号变化极快，需要极宽的带宽（比如 100 MHz）。（数学真理：信息决定需求）但是低频段没有这么宽的连续空闲位置。因此我们必须把载波频率移到高频段（如 28 GHz），那里才有能力提供 100 MHz 的位置供我们使用。（工程现实：位置决定供给）

回到我们最初的困惑，我们可以这样总结这三者的关系：

1. 数据速率的需求 决定了信号 必须占用的带宽宽度。（想运送多少货物，决定了需要多宽的卡车）。
2. 载波频率的选择 决定了我们在频谱的哪个位置 能找到足够宽的道路 来让这辆卡车通过。（低频只有小路，高频有超级高速公路）。

所以，当我们说“Ka 波段带宽大”时，我们是指那个频段有潜力容纳极宽的信号；而当我们说“带宽由信息决定”时，是指一个具体的信号实际需要占用多少空间。两者相辅相成，共同构成了现代高容量通信的基础。

方波和实际带宽

现在我们来讨论数字信号，它通常由类似方波的脉冲组成。一个理论上完美的方波，拥有绝对垂直的上升沿和下降沿。这意味着信号的值是在零时间内瞬间完成跳变的。

1. 无限的变化速度：一个“瞬间”的变化，意味着变化的速度是无限快的。
2. 无限的高频成分：根据傅里叶理论，要完美合成一个无限快的瞬时跳变，你需要叠加频率无限高的正弦波谐波。

因此，一个完美的方波，其带宽是无限大的。当然，在现实世界中，没有任何信道能提供无限的带宽。我们传输的都是一个近似的、带宽有限的方波。

1. 带宽限制 = “削去”高频谐波：真实的信道就像一个滤波器，会自动“砍掉”信号中超过其带宽上限的那些超高频谐波。
2. “不完美”的代价：当高频谐波丢失后，方波的边沿会变缓，拐角会变圆，甚至在平坦部分产生“振铃”（小的波动），就像图中最终合成的那个黑色波形一样。
3. “足够好”即可：幸运的是，我们不需要一个完美的方波。只要带宽足够宽，能保留足够多的关键谐波，使得接收端能够清晰地识别出“高电平(1)”和“低电平(0)”，通信就可以成功。

所以数字信号的数据速率（bps）越高，意味着构成它的方波脉冲就越窄、变化越快。这反过来就需要一个更宽的物理带宽来保留其关键的高频谐波成分，以防信号失真到无法识别。这正是为什么5G通信（追求Gbps速率）比4G（追求Mbps速率）需要分配更宽阔的频谱资源。

功率放大器：无线通信的引擎

能量转换的核心

发射机方框图	接收机方框图

到目前为止，我们已经从信息和数据的视角，理解了射频系统是如何将信息通过“调制”加载到高频载波上，从而实现远距离通信的。现在，让我们切换视角，从更根本的物理和能量层面来审视这个过程。

从能量的角度看，发射机的核心任务，就是将电路中的直流电能高效地转换为向空间辐射出去的电磁波能量。当我们追求极远距离的通信或探测时——例如战斗机的机载雷达需要锁定数百公里外的目标，或者广播塔要覆盖整个城市——就意味着发射出去的电磁波必须携带极其巨大的能量。

我们如何才能产生如此强大的电磁波呢？

答案的源头在天线。正如我们之前所讨论的，天线是通过振荡的电流和电压来产生变化的电场和磁场，从而辐射电磁波的。其辐射能量的强度与天线导体上电流和电压的强度（即功率）直接相关。简而言之，要让电磁波“喊”得更响、传得更远，就必须向天线馈送一个功率足够强大的高频电信号。

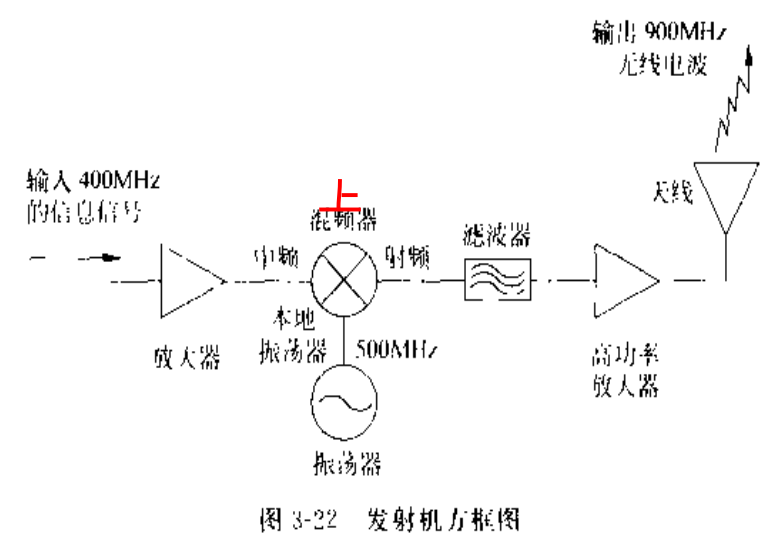
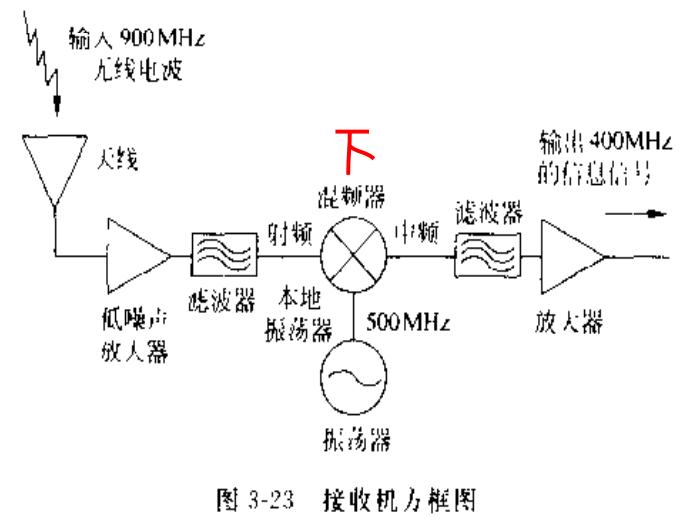
然而，这个最终馈入天线的高功率信号，并不是凭空产生的。在它被发射前的旅程中，它最初其实非常微弱。让我们跟随上图左侧的发射机方框图，看看一个射频信号是如何“诞生”的：

1. 振荡器 (Oscillator)：这是射频系统的心脏。它负责产生一个频率极其稳定、纯净的高频正弦波，也就是我们的载波。在图中，它产生了一个 500 MHz 的“本地振荡”信号。这个信号本身不携带任何信息，它只是一个准备被“装载”的“搬运车”。

2. 混频器 (Mixer)：这是一个进行频率“搬移”的关键部件。它接收两路输入：一路是已经承载了原始信息、频率较低的信号（图中的“输入400MHz的信息信号”，这在实际系统中通常被称为中频信号 IF），另一路就是振荡器产生的载波（本振信号 LO）。混频器将两者“混合”，产生一个新的频率，即射频信号 (RF)。根据混频原理，输出会包含和频与差频，通过滤波器选择我们需要的频率。在这个例子中，它执行的是上变频操作：\(400 \text{ MHz (IF)} + 500 \text{ MHz (LO)} = 900 \text{ MHz (RF)}\)。

经过这一系列处理后，一个携带了特定信息、工作在目标发射频率（900 MHz）上的射FIN信号就诞生了。但此时，它有一个致命的弱点：功率极低。通常，从混频器或更早期的调制器出来的信号功率非常小，典型值可能只有几个毫瓦 (mW)，甚至微瓦 (µW)。在射频工程中，这通常用 dBm 来表示，0 dBm 就代表 1 毫瓦。这个级别的能量，如果直接送到天线，可能连房间的另一头都无法有效通信。

于是，在信号链的最后一环、天线之前的那个至关重要的位置，我们必须部署一个“大力士”——它的任务只有一个：将这个微弱的高频信号，放大成一个拥有足够“肌肉”的强大信号。

这个装置，就是功率放大器（Power Amplifier, PA）。

PA接收这个低功率的射频信号，并以它为模板，输出一个频率和波形完全相同，但功率被放大了成千上万倍的复制品。

• 它放大的是什么？电压还是电流？ 它放大的既是电压也是电流。因为功率 (\(P\)) 是电压 (\(V\)) 和电流 (\(I\)) 的乘积 (\(P = V \times I\))，所以为了实现功率的巨大增益，PA必须同时提升信号的电压和电流驱动能力。因此，它被称为“功率”放大器。

• 能量从何而来？ 这是一个核心问题。根据能量守恒定律，能量不能凭空产生。PA本身并不创造能量，它是一个高效的能量转换器。它从一个外部的直流电源（如电池、电源适配器）获取大量的直流电能，然后在这个微弱的输入射频信号的“指挥”下，将这些直流能量巧妙地转换并附加到输出的射频信号上。

因此，功率放大器是整个发射系统的“引擎”和“心脏”。它连接了微弱的信号处理世界和强大的物理辐射世界，通过消耗直流电能，为最终的电磁波注入了足以跨越山川湖海的澎湃动力。

基础知识回顾

在深入探索功率放大器复杂的工作原理之前，让我们先花点时间，为工具箱补充一些必备的、贯穿整个射频领域的“通用工具”。

分贝 (dB) - 射频工程师的“标尺”

在射频系统中，信号的功率变化范围极其巨大。例如，发射机发射的信号功率，可能是天线最终接收到的信号功率的数万亿倍（甚至更多！）。直接用这么大的数字进行乘除运算既繁琐又容易出错。

因此，在射频领域，我们采用一种更便捷的对数标尺——分贝 (dB)——来表示功率的增益或损耗。其定义如下： \[ \text{增益 (dB)} = 10 \cdot \log_{10}\left(\frac{P_\mathrm{out}}{P_\mathrm{in}}\right) \] 使用分贝，可以将复杂的乘除运算转换为简单的加减法，极大地方便了计算。例如，一个放大1000倍的放大器（+30dB）串联一个衰减100倍的衰减器（-20dB），总增益就是 30 + (-20) = +10dB，即净放大10倍。

在日常工程中，有两个经验法则最为常用：

• +3 dB ≈ 功率变为 2 倍
• +10 dB ≈ 功率变为 10 倍

此外，为了表示一个信号的绝对功率，我们使用 dBm。它是一个以 1毫瓦 (mW) 为基准的分贝值。

• 0 dBm = 1 mW (基准点)
• 10 dBm = 10 mW
• 20 dBm = 100 mW
• 30 dBm = 1000 mW = 1 W

电路分析定律 - 从宇宙真理到工程实践

我们熟悉的直流电路遵循简单的欧姆定律。然而，功率放大器是一个包含复杂有源器件（晶体管）的交流电路，其行为是非线性的。幸运的是，我们不需要每次都从最底层开始分析，只需掌握一套分层次的法则，即可理解功放电路。

层次一：宇宙的终极法则 —— 麦克斯韦方程组

这是射频、电磁学世界里唯一的、永恒的、绝对的真理。

它是由四个方程组成的方程组，是整个电磁世界的“宪法”。所有的电学、磁学、光学现象，包括我们后面要谈到的基尔霍夫定律和欧姆定律，都只是它在特定条件下的简化特例。对于射频工程，它从第一性原理层面解释了一切：

• 电磁波的传播：它预言了电磁波的存在，并揭示了光和无线电的本质。
• 天线的辐射：它解释了天线如何将电路中的能量有效地转换为空间中的电磁波能量。
• 串扰与耦合：它解释了为何高频信号能“凭空”影响相邻的导线，因为能量是通过电磁场传递的。
• 趋肤效应：它解释了为何高频电流倾向于在导体的表面流动。

层次二：电路世界的实用法则 —— 基尔霍夫定律 + 复阻抗

尽管麦克斯韦方程组是终极真理，但在分析集总电路（元件尺寸远小于波长的电路）时，我们无需动用这门“屠龙之技”。一套更实用的法则足以应对：

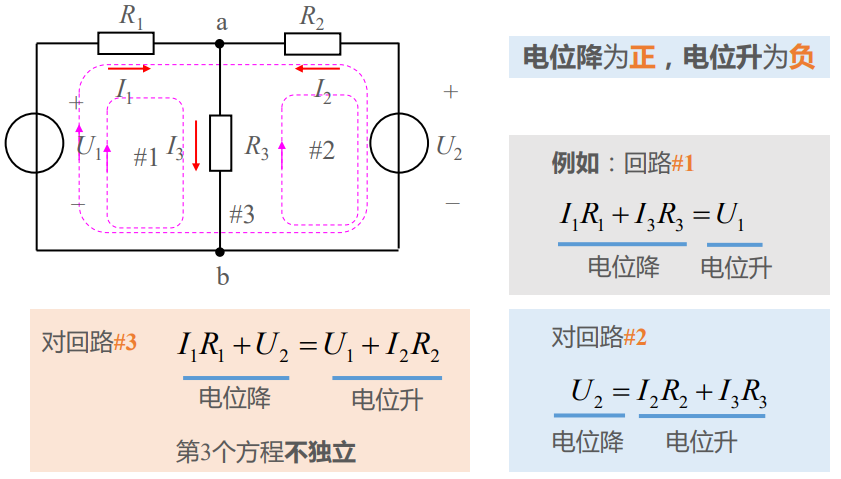
1. 基尔霍夫定律 (Kirchhoff's Laws)

这两条定律源自电荷守恒和能量守恒，在任何电路中都永不失效。

• 电流定律 (KCL): 流入一个节点的电流之和等于流出电流之和。
• 电压定律 (KVL): 沿任何闭合回路的电压升与电压降代数和为零。

基尔霍夫电流定律 (KCL)	基尔霍夫电压定律 (KVL)

2. 交流欧姆定律 (V = I · Z) —— Ohm's Law的进化形态

在直流世界里，欧姆定律 (\(V=IR\)) 简单而完美。但在交流世界，当电感(L)和电容(C)加入后，情况变得复杂。因为电感和电容对电流的“阻碍”行为，并不仅仅是“电阻”，它们还会引入相位差：

• 在电感中，电压的相位会超前电流 90°。
• 在电容中，电压的相位会落后电流 90°。

为了在一个统一的框架下，既能描述幅度关系，又能描述相位关系，我们引入了强大的数学工具——复数。我们将交流电压和电流表示为包含幅度和相位的相量 (Phasor)，并定义了复阻抗 (Z)。

复阻抗 \(Z\) 是一个复数，通常写作 \(Z = R + jX\)：

• 实部 R (电阻, Resistance): 这是我们所熟悉的、会产生热量的“真实”电阻。它代表电路中消耗并转化为热能的部分。流过它的电流和它两端的电压始终是同相的。

• 虚部 X (电抗, Reactance): 这是交流电路独有的部分，代表由电感和电容产生的“阻碍”效应。它不消耗能量，只进行能量的暂时存储和释放。

  • 感抗 (\(X_L = \omega L = 2\pi fL\)): 由电感产生，为正值。频率越高，感抗越大。它使电压超前电流。
  • 容抗 (\(X_C = -1/\omega C = -1/2\pi fC\)): 由电容产生，为负值。频率越高，容抗越小。它使电压落后电流。

通过复阻抗，我们将 R、L、C 的行为统一到了一个框架下。V = I · Z 这条“进化版”的欧姆定律，允许我们使用与直流电路完全相同的分析方法（如基尔霍夫定律）来解决复杂的交流电路问题，只不过所有的计算都在复数域中进行。这使得我们能用一个公式，同时解出电路中各处的电压、电流的幅度和相位。

层次三：器件的个性法则 —— 非线性器件模型

对于晶体管这样的有源、非线性器件，简单的 V=IZ 完全不适用。我们需要一套专门描述它“个性脾气”的法则——器件模型。例如MOSFET的平方律模型 Id = k * (Vgs - Vth)²，它描述了输出电流Id如何被输入电压Vgs所控制，这是一个典型的非线性关系。

在这里，我们着重讨论一下天线。天线是一个非常特殊的器件，它横跨了两个世界：对电路而言，它是一个负载；对空间而言，它是一个能量转换器。为了能在电路图中分析天线，工程师们建立了一个极其巧妙的等效模型——输入阻抗 (\(Z_\mathrm{in}\))。

从功率放大器的输出端看过去，天线的接线端子表现出的所有电学特性，都可以等效为一个复阻抗 \(Z_\mathrm{in}\)。这个 \(Z_\mathrm{in}\) 就是PA“看到”的负载。 \[ Z_\mathrm{in} = R_\mathrm{in} + jX_\mathrm{in} \] 这个阻抗的两个部分，有着非常深刻的物理意义：

• 虚部 \(X_\mathrm{in}\) (输入电抗): 代表在天线近场（紧邻天线体的区域）来回“振荡”而未辐射出去的能量。这部分能量在电源和天线之间来回交换，是无功功率的来源。在天线设计和匹配中，我们的首要目标通常是让 \(X_\mathrm{in} = 0\)，以确保能量能最有效地传递给天线。

• 实部 \(R_\mathrm{in}\) (输入电阻): 这是模型的精髓所在。它代表所有从电路中被取走且永不返回的功率。这部分功率有两个去向，因此我们可以把它进一步分解为：

\[ R_\mathrm{in} = R_\mathrm{rad} + R_\mathrm{loss} \]

• \(R_\mathrm{loss}\) (损耗电阻): 这是一个真实的物理电阻。它代表了天线导体材料（如铜）自身的电阻，以及绝缘材料的介电损耗。流过这部分电阻的功率，会转化为热量，是被浪费掉的、我们不希望看到的功率。
• \(R_\mathrm{rad}\) (辐射电阻): 这是一个等效的、虚拟的电阻。它本身并不存在于天线的材料中，你无法用万用表测出它。它是一个数学上的概念模型，用来量化天线将电能成功转化为电磁波能量并辐射到空间中去的能力。

所以，为了计算天线实际辐射出去的功率，我们引入了这个等效的“辐射电阻”。 我们可以像分析普通电阻一样，计算流过天线的输入电流 \(I_\mathrm{in}\)。那么：

• 天线总共接收到的有功功率是：\(P_\mathrm{total} = \frac{1}{2}|I_\mathrm{in}|^2 \cdot R_\mathrm{in}\)
• 其中，真正辐射出去的有用功率是：\(P_\mathrm{rad} = \frac{1}{2}|I_\mathrm{in}|^2 \cdot R_\mathrm{rad}\)
• 因为发热而浪费掉的功率是：\(P_\mathrm{loss} = \frac{1}{2}|I_\mathrm{in}|^2 \cdot R_\mathrm{loss}\)

电功率 - 能量转换的语言

功率的计算是射频工程的核心，因为功率放大器的本质就是进行能量转换。

一个器件的瞬时功率由一个普适的、永恒的公式给出： \[ P(t) = U(t) \cdot I(t) \] 这个公式，如同力学中的 P(t) = F(t)·v(t)，是物理世界的基本定律。无论对于何种器件（电阻、电容、晶体管、天线），其在任何瞬间消耗或产生的功率，永远是该瞬间其两端电压与流过电流的乘积。

在交流电路中，由于电压和电流随时间周期性变化，且可能存在相位差，瞬时功率的平均效果就变得十分有趣。这就引出了三个关键的功率概念：

• 瞬时功率 (p(t)) 就是上面定义的 U(t) · I(t)。它表示在任意时刻，能量流动的速率和方向。它可能是正值（电源向负载输送能量），也可能是负值（负载向电源返还能量）。

• 有功功率 / 平均功率 (P) 也称为“实功”，它是在一个完整周期内，瞬时功率的平均值。这部分功率是真正被消耗掉并转化为其他形式能量的功率，例如：

  • 在电阻上，它转化为热能。
  • 在天线的辐射电阻上，它转化为电磁波能量并辐射出去。
  • 在电动机中，它转化为机械能。 有功功率的单位是瓦特 (W)。如上表所示，纯电阻负载上消耗的就是有功功率。

• 无功功率 (Q) 这部分功率并不做“有用功”，它不产生热量也不辐射出去。它是在一个周期内，电源与电抗性元件（电感、电容）之间来回“交换”或“暂存”的能量。

  • 在一个半周期，电源为电感（建立磁场）或电容（建立电场）充电，能量从电源流向负载。
  • 在另一个半周期，电感（磁场塌缩）或电容（电场消失）放电，将储存的能量返还给电源。 虽然无功功率的周期平均值为零，但它的存在是建立交变电磁场和维持电路正常工作所必需的。它的单位是乏 (var)，即伏安无功。

对于功率放大器而言，它的目标就是将直流电源提供的有功功率，高效地转换为射频信号的有功功率，并最终通过天线辐射出去。而电路中的电感电容所产生的无功功率，虽然是必要的，但过多的无功功率会增加电路损耗，降低效率，是设计中需要仔细管理和匹配的部分。

阻抗匹配 - 最高效的能量传输之道

我们已经知道，功率放大器的核心任务是向负载（通常是天线）输送尽可能大的功率。但这不仅仅是“推得更用力”那么简单。在电源和负载之间，存在一个深刻的物理法则，决定了能量能否被高效地传递，这个法则就是阻抗匹配。

1. 直流世界：简单的功率拔河

想象一个最简单的电路：一个有内阻的真实电源，连接到一个负载电阻上。

• \(V_s\): 理想电压源，代表能量的源头。
• \(R_s\): 电源内阻 (Source Resistance)。可以看作是电源内部固有的、会消耗能量的“摩擦力”。
• \(R_L\): 负载电阻 (Load Resistance)。这是我们想要把能量传递给的对象。

我们的目标是： 调整负载 \(R_L\) 的大小，使得 \(R_L\) 上消耗的功率 \(P_L\) 达到最大化。

通过简单的电路分析可以发现一个有趣的“拔河”现象：

• 当负载电阻 \(R_L\) 太大时 (接近开路):
  • 虽然负载分得了很高的电压，但整个回路的电流 I 变得极小。根据 \(P_L = I^2 R_L\)，一个极小的电流无法产生显著的功率。能量无法有效流出。
• 当负载电阻 \(R_L\) 太小时 (接近短路):
  • 整个回路的电流 I 变得很大，但绝大部分能量都被电源内阻 \(R_s\) 自身以发热的形式消耗掉了。负载几乎没有获得功率，我们只是在给电源“加热”。
• 当负载电阻等于电源内阻 (\(R_L = R_s\)) 时 —— 完美匹配！
  • 通过微积分可以严格证明，此时负载获得的功率 \(P_L\) 达到最大值。
  • 在这个最佳状态下，电源产生的总功率中，50% 被成功传递给了负载，另外 50% 则消耗在了自身的内阻上。这听起来效率不高（只有50%），但这已经是我们能从这个真实电源中“榨取”出的最大外部功率了。

这就是直流世界中的最大功率传输定理。

2. 交流世界：与“电抗”共舞

进入交流世界，情况变得更加复杂。我们的阻抗不再是简单的电阻 R，而是包含了电抗 X 的复阻抗 Z = R + jX。

假设一个更真实的射频场景：

• \(Z_s = 50 + j25 \Omega\): 我们的功放（电源）输出阻抗是50Ω，但它还带有一个+j25的感性部分（代表输出引脚的寄生电感）。
• \(Z_L = 100 - j50 \Omega\): 我们的天线（负载）输入阻抗是一个100Ω的电阻，但它还带有一个-j50的容性部分（代表天线输入端的寄生电容）。

在交流电路中，最大功率传输的条件变得更加严格，它要求负载阻抗必须等于电源阻抗的复共轭。 \[ Z_L = Z_s^* \] 如果 \(Z_s = R_s + jX_s\)，那么它的共轭 \(Z_s^* = R_s - jX_s\)。这个目标可以分解为两步：

1. 电阻部分匹配: \(R_L = R_s\)。这和直流世界的结论一样，保证了有功功率的传输通道是通畅的。
2. 电抗部分“抵消”: \(X_L = -X_s\)。这是全新的、至关重要的部分！

“抵消”的物理意义：谐振 (Resonance)

电抗（jX）的本质是不消耗能量，只进行能量的暂时存储和释放。

• 电源的感性电抗 +jX_s 像一个弹簧，在一个半周期内压缩（储存能量），在另一个半周期内释放。
• 负载的容性电抗 -jX_L 则像另一个特性相反的弹簧。

当 \(X_L = -X_s\) 时，这两个“弹簧”的动作完美互补。在一个周期内，从电源侧电感释放的能量，正好被负载侧电容吸收；反之亦然。这些“无功”的能量在两者之间形成了完美的内部循环，自给自足。从整个电路的角度看，这两个电抗的效应互相抵消了，总的电抗为零！能量得以顺畅地从电源的 \(R_s\) 传递到负载的 \(R_L\)，不再需要去克服电抗的“阻碍”。

3. 匹配网络：电路的“翻译官”

在上面的例子中，电源和负载显然既不相等也不共轭。如果直接连接，能量传输效率会极低。此时，我们必须在它们之间插入一个由无源、无损的电感(L)和电容(C)组成的匹配网络 (Matching Network)。

         Z_s                [ Matching Network ]               Z_L
Source --(50+j25)--o---------|   由 L 和 C 组成   |----------o--(100-j50)-- Load

这个匹配网络如同一个精巧的“翻译官”或“变速箱”，它的神奇任务是：将负载 \(Z_L\) “伪装”成电源 \(Z_s\) 最希望看到的那个阻抗。

也就是说，它需要把自己和 \(Z_L\) 打包在一起，使得从电源 \(Z_s\) 的“视角”向右看过去，看到的等效阻抗正好是 \(Z_s\) 的共轭，也就是 \(50 - j25 \Omega\)。当匹配网络设计正确时：

• 电源 Z_s = 50 + j25 Ω 看向右边，看到了它梦寐以求的 50 - j25 Ω。
• +j25 和 -j25 的电抗在接口处完美抵消（谐振）。
• 50Ω 的源电阻看到了一个 50Ω 的等效负载电阻。
• 最大功率传输得以实现！

4. 史密斯圆图：射频工程师的寻宝图

我们已经确定，必须在电源和负载之间插入一个“电路翻译官”——匹配网络。但这个网络该如何设计呢？我们总不能靠着试错来焊接电感和电容吧？

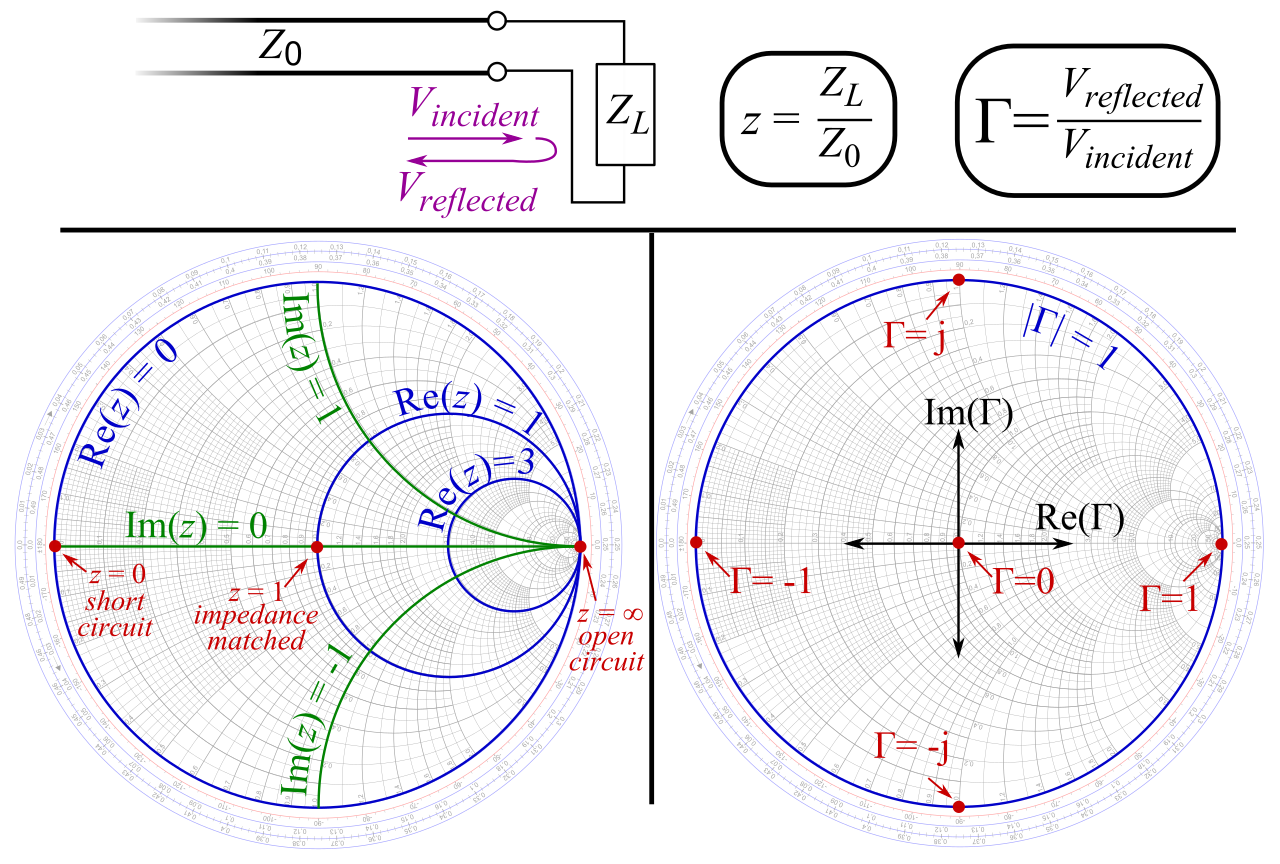
这时，我们就需要请出射频工程师的“寻宝图”——史密斯圆图 (Smith Chart)。

第一眼看到它，可能会觉得头晕目眩，像一张复杂的天体运行图。但一旦理解了它的语言，它就会成为我们设计匹配网络时最直观、最强大的导航工具。它的核心思想，就是将所有可能的复阻抗（Z = R + jX）都映射到这一个圆形的图表上。

让我们对照上图，把这张图拆解开来看：

1. 中心点 (Reference Impedance, Γ=0)：图表的最中心，就是我们梦寐以求的“宝藏”所在地。这个点代表完美匹配（在50Ω系统中，它就是50Ω）。在这里，反射系数(Γ)为零，意味着所有能量都被顺利传输，没有任何反射。
2. 最外圈 (Total Reflected Signal, |Γ|=1)：这是最糟糕的情况，代表完全反射。任何落在最外圈上的阻抗（比如短路 R=0 或开路 R=∞）都会将所有能量反弹回来。
3. 水平中轴线：这条线代表纯电阻世界，没有任何电抗（jX = 0）。中心是50Ω，最左端是0Ω（短路），最右端是无穷大Ω（开路）。
4. 恒定电阻圆 (Constant Resistance circles)：图中的这一系列圆形，每个圆上所有点的电阻R值都是相同的。中心点的那个圆是R=1（标准化后为50Ω），越往右的圆代表的电阻值越大。
5. 恒定电抗弧 (Constant Reactance arcs)：从最右侧发散出来的这些弧线。每条弧线上所有点的电抗X值都是相同的。
   • 上半圆（灰色区域）：代表感性电抗 (+jX)。越往上，电感性越强。
   • 下半圆（橙色区域）：代表容性电抗 (-jX)。越往下，电容性越强。

所以，任何一个复阻抗，比如 \(100 - j50 \Omega\)，都能在这个图上通过一个电阻圆和一个电抗弧的交点，找到它唯一的坐标。

设计匹配网络的过程，在史密斯圆图上就变成了一个非常直观的“寻路游戏”：从代表负载阻抗的“起点”，通过添加元件，一步步“走”到我们想要的“终点”。

“走路”的规则非常简单：

• 串联一个电感：从当前的点，顺时针沿着所在的“恒定电阻圆”移动。
• 串联一个电容：从当前的点，逆时针沿着所在的“恒定电阻圆”移动。

在开始我们的实际案例前，先回答几个关键问题：

1. 是不是只能串联？可以并联吗？ 当然可以！并联电路也非常常用。在史密斯圆图上处理并联会稍微复杂一点，通常需要切换到它的“对偶”——导纳图（可以简单理解为把整个图旋转180°）。在导纳图上，并联电容和电感也有着类似“顺时针/逆时针”的简单移动规则。很多时候，一个“串联+并联”的组合拳（即L型网络）是最高效的匹配方式。

2. 为什么只加电感(L)和电容(C)，不加电阻(R)？ 这是一个核心概念！我们的目标是做“翻译官”，而不是“收费站”。电感和电容是无损元件，它们只储存和释放能量，不消耗能量。而电阻是有损耗的，它会把宝贵的射频能量变成热量耗散掉。我们的目标是最大化功率传输，所以匹配网络必须由无损的L和C组成。

现在，让我们用这张“寻宝图”来解决之前的案例。

• 起点 (负载): \(Z_L = 100 - j50 \Omega\)。标准化后为 \(z_L = \bf{2 - j1}\)。
• 终点 (目标): \(Z_{target} = 50 - j25 \Omega\)。标准化后为 \(z_{target} = \bf{1 - j0.5}\)。

我们的旅程开始：

1. 定位起点A: 在图上找到“电阻圆R=2”和“电抗弧X=-1”的交点。它在图的右下方橙色区域。
2. 定位终点B: 在图上找到“电阻圆R=1”和“电抗弧X=-0.5”的交点。它在中心点靠下的位置。
3. 规划路径: 我们需要从A点走到B点。这里有无数条路径，对应着不同的匹配网络设计。我们选择一种简单的“两步走”策略：
   • 第一步：串联一个电感。我们从A点(\(2-j1\))出发，沿着它所在的r=2电阻圆，顺时针移动（增加感性电抗）。我们一直走到与终点B所在的r=1电阻圆相交的那个点，我们称之为中间点C。
   • 第二步：串联一个电容。现在我们位于C点。从这里，我们沿着r=1电阻圆逆时针移动（增加容性电抗），直到我们精确地落在终点B(\(1-j0.5\))上。

旅程结束！ 我们通过在图上画出的这两段弧长，就可以直接换算出第一步需要串联的电感值（单位nH）和第二步需要串联的电容值（单位pF）。这样，一个复杂的复数运算问题，就这样被我们转化成了一个直观的、在地图上从A点走到B点的寻路问题。这就是史密斯圆图的魅力所在——它让抽象的阻抗匹配变得触手可及。

5. 失配的灾难性后果：能量反射

你可能会问一个很深刻的问题：“不都是电路吗？为什么低频电路失配只是效率低，到了射频这里就会有什么‘反射’，甚至造成‘灾难性’后果呢？”

这个问题的核心在于信号的波长。

• 在低频电路中（比如50Hz交流电），信号的波长长达数千公里。相对于我们几厘米的电路板，整个电路就像一个“点”，电压变化是瞬间同步的。这叫集总参数电路。
• 但在射频领域（比如2.4GHz WiFi），信号波长只有12.5厘米，和我们电路板上的走线长度在同一个数量级。信号不再是瞬间同步的，而是像波浪一样在走线（我们称之为“传输线”）上传播。这叫分布式参数电路。

现在，想象一下你正晃动一根长长的绳子，制造出一个波形向前传播。

如果绳子的另一端连接着一根完全相同的绳子，波形会顺滑地传递过去，这就是阻抗匹配。但如果绳子的另一端是系在一堵墙上（阻抗突变），波形到达墙壁时会怎么样？它会被反射回来！

在射频电路里，传输线就是这根绳子，电磁波就是绳子上的波形。当电磁波从50Ω的传输线，突然遇到一个\(100 - j50 \Omega\)的天线时，这个阻抗突变点就像一堵“墙”，一部分能量无法被吸收，只能被反射回来。

结合上图，这个过程会产生一系列可以用精密仪器测量的参数，它们都在描述失配的严重程度：

• 反射 (Reflection)：图中 Reflected A 就是被弹回来的能量波。它的大小由反射系数 (Γ 或 S11) 来描述。反射系数为0代表完美匹配。
  • 驻波比 (SWR)：入射波和反射波在传输线上干涉，会形成“驻波”（某些点电压始终很高，某些点很低）。SWR就是衡量驻波严重程度的指标，是失配最经典的“症状”。SWR=1代表完美匹配。
  • 回波损耗 (Return Loss)：从另一个角度描述反射有多弱。回波损耗越大，说明反射回来的能量越小，匹配效果越好。
• 传输 (Transmission)：图中 Transmitted B 才是我们真正想要的、成功被负载（天线）接收的能量。它的大小由传输系数 (T 或 S21) 描述。
  • 插入损耗 (Insertion Loss)：衡量了因为失配等原因，有多少能量在传输过程中损失掉了。

最后，为什么这对功率放大器是“灾难性的”？

功率放大器就像一个单向的高压水泵，它的输出级晶体管被设计用来将能量奋力地“推”出去。但它天生就很脆弱，完全没有为承受反向回来的能量做准备。

当严重失配发生时，巨大的反射能量会像一道冲击波，沿着传输线原路返回，狠狠地撞在功放的输出级上。这股无处可去的能量只能在脆弱的晶体管内部转化为剧烈的热量。对于一个本就在高功率下工作的功放，这股额外的热量是致命的，会导致其温度瞬间飙升，轻则性能下降、信号失真，重则永久性烧毁！

这就是为什么在射频工程，尤其是在大功率应用中，阻抗匹配不是一个“锦上添花”的选项，而是一个必须严格遵守的“生死法则”。

电路等效 - “化繁为简”的分析利器

在功放电路分析中，我们将面对一个“混合”的世界：一个强大的直流电源与一个微弱的交流信号在同一个晶体管中共存。 * 直流电源负责为晶体管“供电”，使其建立一个稳定的静态工作点 (Quiescent Point, or Bias)，让它处于准备好工作的“待命”状态。 * 微弱的交流信号（我们的输入信号）则在这个静态工作点的基础上进行摆动，晶体管接收这个小信号，并利用直流电源提供的能量，将其放大为一个强大的交流输出信号。

要同时分析这种直流和交流叠加的复杂情况是非常困难的。因此，工程师们采用了一种极其有效且优雅的“分而治之”策略：利用电路等效原理，将复杂的混合电路分解为两个更简单的、可以独立分析的电路。

1. 直流通路：建立电路的“舞台” (Biasing Analysis)

分析目标： 确定晶体管的静态工作点 (Q-point)。这个工作点由直流电压和直流电流（如 \(I_\mathrm{DQ}\), \(V_\mathrm{DSQ}\)）定义，它决定了晶体管的工作模式和基本性能，是整个放大器性能的基石。

为了只看直流部分的影响，我们必须暂时“忽略”所有交流相关的元件。我们遵循以下等效规则：

• 电容视为开路： 一个理想的电容器在直流电压下，一旦充电完成，就不会再有稳态电流流过。因此，在直流分析中，所有电容器都相当于断开的电路。
• 电感视为短路： 一个理想的电感器对于直流电流来说，没有阻碍作用，就如同一根导线。因此，在直流分析中，所有电感器都相当于短路。
• 交流信号源视为短路： 根据叠加原理，在分析直流电源的作用时，我们应将其他独立电源的效果置零。对于一个理想的交流电压源，其直流分量为零，因此等效为短路。（若信号源有内阻，则保留其内阻）。

通过这些规则，我们可以得到一个纯粹的直流通路，并用简单的直流电路法则（如欧姆定律、基尔霍夫定律）计算出电路中各点的静态电压和电流。

2. 交流通路：上演“放大”的戏剧 (Small-Signal Analysis)

分析目标： 研究电路的动态参数，如增益、输入/输出阻抗、频率响应等。这是分析电路作为“放大器”性能的核心。

现在，我们的视角切换到那个在静态工作点上叠加的、微小的交流信号。我们只关心信号的“变化量”，而不再关心绝对的直流数值。因此，我们遵循一套新的等效规则：

• 容量大的电容视为短路： 耦合电容或旁路电容的容值通常很大。对于高频的交流信号，其容抗 \(X_C = 1/(2\pi fC)\) 会变得非常小，与电路中其他电阻相比可以忽略不计。因此，我们将其近似为交流信号的通路——短路。

• 无内阻的直流电压源视为短路 (AC Ground)： 这是最关键也最巧妙的一步。一个理想的直流电压源，其定义是“无论流过多少电流，其两端电压永远保持恒定”。

  • 从交流信号的视角来看，交流信号是一种“电压的变化”。既然直流电源两端的电压恒定不变，那么它两端的电压变化量永远为零。
  • 在电路中，一个两端电压差永远为零的元件，其定义就是短路。
  • 因此，对于交流信号而言，直流电源的正极（或负极）是一个电位稳定点，我们称之为“交流地” (AC Ground)。

一个至关重要的澄清：

将直流电源视为“交流地”，不代表我们忘记了它的存在。恰恰相反，这个直流电源的影响已经深深地“烙印”在了我们的交流分析之中：

直流偏置决定了静态工作点，而静态工作点决定了晶体管在此处的“小信号模型参数”（如跨导\(g_m\)、输出电阻\(r_o\)等）。我们正是使用这些由直流决定的参数，来进行后续的交流分析的。

通过以上规则，我们可以画出一个纯粹的交流通路图，并在这个等效电路上计算放大器的各项动态性能指标。这个强大的分析方法，将一个复杂的非线性电路问题，成功地简化为了两个线性电路问题的组合，是我们后续理解功放电路的必备工具。

晶体管作为功放：核心的有源器件

在现代电子学中，功率放大器几乎总是使用晶体管（或其前身电子三极管）来构建。我们将以最常见的场效应晶体管 (MOSFET) 为例，深入剖析其作为放大器的核心工作原理。要理解功放电路，首先必须理解其核心元件——晶体管的“个性脾气”。

1. 物理图景：一个由电压控制的“阀门”

晶体管有三个电极：栅极 (Gate, G)、漏极 (Drain, D) 和 源极 (Source, S)。其工作的本质，是利用栅极的电场来控制源极和漏极之间导电沟道的“开”与“关”，以及“开”的大小。

一个非常有效的心智模型是：不要把晶体管看作一个复杂的三端器件，而要把它看作一个可调节的两端器件。

想象一下，源极和漏极之间是一条水管。而栅极，就是控制这条水管水流的阀门。栅极本身几乎没有水流通过（栅极电流极小），但你转动阀门的角度（栅极电压 \(V_{GS}\)），却能精确地控制水管中水流的大小（漏极电流 \(I_{DS}\)）。

这个“压控阀门”的特性，可以通过其“说明书”—— I-V 特性曲线 —— 来完整描述。

MOSFET 输出特性曲线	MOSFET 转移特性与输出特性

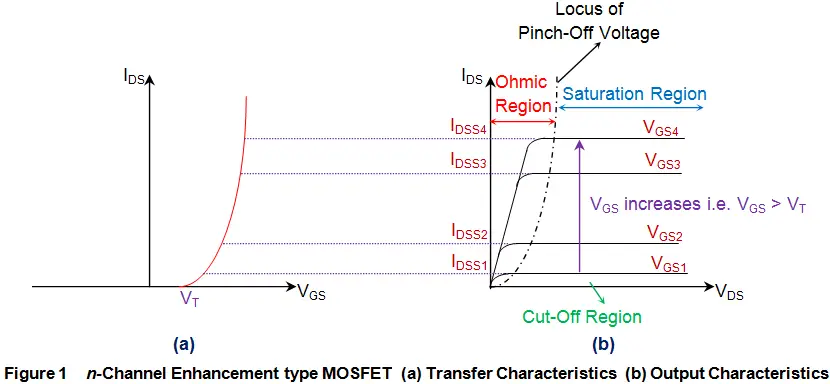上图左侧的输出特性曲线 (\(I_{DS}\) vs \(V_{DS}\)) 展示了晶体管作为“阀门”的三种工作状态：

1. 截止区 (Cut-off Region):

   当栅极电压 \(V_{GS}\) 低于一个阈值电压 \(V_T\) 时，阀门是完全关闭的。源极和漏极之间的导电沟道没有形成。此时，无论你在水管两端施加多大的水压（漏极电压 \(V_{DS}\)），都不会有水流（漏极电流 \(I_{DS}\)）通过。

2. 线性区 / 欧姆区 (Linear / Ohmic Region):

   当栅极电压 \(V_{GS}\) 超过阈值电压，阀门被打开。在漏极电压 \(V_{DS}\) 还比较低的时候，水流的大小不仅取决于阀门的开度 (\(V_{GS}\))，也大致正比于水压 (\(V_{DS}\))。此时，晶体管的行为类似一个可变电阻，其电阻值由栅压 \(V_{GS}\) 控制。这个区域对于用作电子开关非常重要。

3. 饱和区 (Saturation Region):

   这才是放大器的“甜蜜点”。当漏极电压 \(V_{DS}\) 增加到足够大之后，一个奇妙的现象发生了：沟道中的电流达到了一个饱和值。此时，电流的大小几乎不再随漏极电压 \(V_{DS}\) 变化，而只取决于栅极电压 \(V_{GS}\) 的大小。在这个区域，晶体管完美地扮演了一个压控电流源 (Voltage-Controlled Current Source) 的角色：你给栅极一个确定的电压，它就在漏极输出一个确定的、不受输出端电压影响的电流。这就是放大作用的物理基础。

   在我们的阀门比喻中，这就好比水压已经大到足以将阀门在当前开度下能通过的水流全部“吸走”。此时，水流的大小只取决于阀门的开度，再增加水压也无法让水流变得更大。

2. 放大作用的实现：从转移特性说起

我们把晶体管工作在饱和区的特性单独拿出来，绘制成转移特性曲线（上图右部分，\(I_{DS}\) vs \(V_{GS}\)）。这条曲线直接描绘了“控制”与“结果”之间的关系。

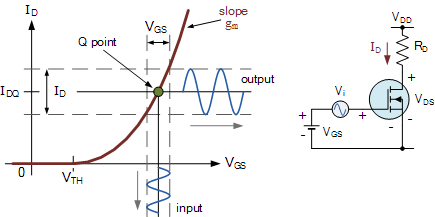
放大的过程如下：

1. 建立静态工作点 (Q-point): 我们首先通过直流电源，给栅极一个固定的直流偏置电压 \(V_{GSQ}\)。这相当于预先将“阀门”拧到一个合适的初始开度，使得电路中有一个稳定的直流“静态”电流 \(I_{DQ}\) 在流动。这个点，就是图中的 Q 点。
2. 叠加输入小信号: 然后，我们将一个微弱的、随时间变化的交流信号（input）叠加在这个直流偏置上。这使得栅极电压在 \(V_{GSQ}\) 上下进行小范围的摆动。
3. 获得放大输出: 由于转移特性曲线在 Q 点附近是陡峭的，栅极电压的这个“小摆动”，会通过晶体管的“杠杆作用”，引起漏极电流在 \(I_{DQ}\) 上下一个大得多的摆动（output）。

我们就这样，成功地将一个微弱的输入电压变化，转换为了一个强大的输出电流变化。 这就是晶体管作为放大器的本质。

3. 量化放大能力：跨导 (\(g_m\))

那么，这个“杠杆作用”的强度如何量化呢？我们用跨导 (\(g_m\)) 这个参数来描述。

跨导的定义是，在工作点 Q 处，转移特性曲线的斜率。它精确地描述了输出电流对输入电压的“敏感程度”。 \[ g_m = \frac{\partial I_D}{\partial V_{GS}}\Bigg|_{V_{DS}=\text{const}} \]

• 单位: 跨导的单位是安培/伏特 (A/V)，这个单位被命名为西门子 (S)。
• 物理意义: \(g_m\) 的意义非常直观——“输入端栅极电压每变化 1 伏特，能引起输出端漏极电流变化多少安培”。它就是晶体管的核心“放大系数”。\(g_m\) 越大，晶体管的电压-电流转换能力就越强，放大能力也越强。
• 典型范围: 跨导的值取决于晶体管的类型、尺寸和工作点。对于小信号射频晶体管，其值通常在几十到几百毫西门子 (mS)。而对于需要驱动大电流的功率管，其跨导可以达到数个西门子 (S)。

如上图所示，跨导 \(g_m\) 并非一个常数，它会随着栅极偏置电压 \(V_G\) 的变化而变化。通常，随着栅压的增加，跨导会先快速增加，进入一个相对平坦的高增益区，最后由于各种物理效应而再次下降。为获得稳定且高效率的放大，工程师需要精心选择静态工作点，使晶体管工作在最佳的跨导区域。

4. 晶体管的速度极限：频率相关特性

我们已经建立了一个强大的心智模型：晶体管是一个由电压控制的电流源。然而，这个模型隐含了一个假设——晶体管的响应是瞬时的。在现实世界中，任何物理过程都需要时间。如果输入信号变化得太快，晶体管就会“跟不上”，其放大能力会急剧下降。这种固有的速度极限，决定了功率放大器的最高工作频率。

主要有两个物理因素限制了MOSFET的速度。

因素一：沟道渡越时间（通常不是瓶颈）

第一个，也是最直观的限制，是载流子（电子）物理地从源极穿行到漏极所需要的时间。这被称为渡越时间 (Transit Time)。 \[ \tau_t = \frac{L}{v_{sat}} \] 其中 \(L\) 是沟道长度，\(v_{sat}\) 是电子的饱和漂移速度。对于一个典型的现代晶体管，假设 \(L=1 \mu m\)，\(v_{sat} \approx 10^7 \text{ cm/s}\)，计算出的渡越时间仅为10皮秒(ps)。这对应于一个高达100 GHz的理论极限频率。虽然这是一个真实存在的物理极限，但对于绝大多数应用场景，存在一个比它影响大得多的限制因素。

因素二：寄生电容（真正的罪魁祸首）

真正的性能瓶颈在于晶体管自身内部、不可避免的寄生电容 (Parasitic Capacitance)。一个真实的晶体管，其物理结构是由半导体、绝缘层和金属层堆叠而成，这种结构天生就在其各个电极之间形成了微小的电容器。

为了分析这些寄生电容的影响，我们需要使用一个高频小信号等效电路。这个模型是一个电路“漫画”，它精准地抓住了晶体管在直流偏置点附近，对交流信号所表现出的核心行为。我们使用一个简化版的模型来获得清晰的物理图像，暂时忽略输出电阻(\(r_{ds}\))等次要效应。

晶体管符号	高频小信号等效模型

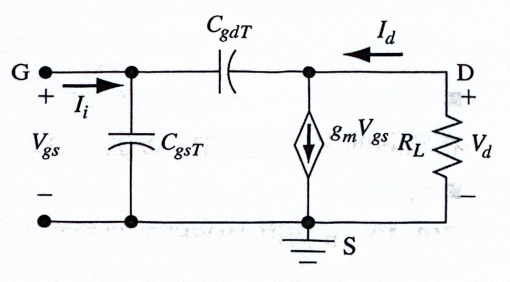让我们一步步拆解这个等效模型：

1. 放大引擎 (\(g_m V_{gs}\)): 右侧那个菱形的符号是放大作用的核心。它就是我们前面定义的压控电流源。它在输出端（漏极D到源极S）产生一个交流电流 \(I_d\)，其大小正比于输入的交流电压 \(V_{gs}\) 和晶体管的跨导 \(g_m\)。

2. 寄生电容: 这些不是我们额外添加的元件，而是晶体管物理结构的一部分。

   • \(C_{gsT}\) (栅源电容): 由栅极金属、栅氧化层和源极/沟道区域共同构成。为了改变栅极的电压，我们必须先对这个电容进行充电或放电，这需要时间。
   • \(C_{gdT}\) (栅漏电容): 由栅极和漏极之间的交叠区域形成。这个电容虽然通常很小，但却是最麻烦的一个，因为它在放大器的输出和输入之间建立了一条“反馈”路径。

随着输入信号频率 \(f\) 的升高，这些电容的容抗 \(X_C = 1/(2\pi fC)\) 会变得越来越小，它们开始像“短路”一样，分流了本该用于控制的信号，从而限制了晶体管的放大能力。

米勒效应：被放大了的寄生电容

现在，我们通过分析电路来精确找出频率的极限。我们的目标是建立输入电流 \(I_i\) 和有用的输出电流 \(I_d\) 之间的关系。为此，我们使用基尔霍夫电流定律(KCL)，即流入一个节点的电流总和必须等于流出该节点的电流总和。

【KCL电路分析小贴士】

分析时，我们先确立一个电流方向的惯例。例如，我们规定流入节点的电流为正，流出节点的电流为负。在栅极(G)节点，输入电流 \(I_i\) 是流入的。而流经两个电容的电流是流出的。因此，可以写出方程：\(I_i - I_{Cgs} - I_{Cgd} = 0\)。再利用电容的交流电流公式 \(I_C = j\omega C \cdot V_C\)（其中\(V_C\)是电容两端的电压），就可以得到下面的方程组。

如你所列出的，通过在栅极(G)和漏极(D)节点上应用KCL，并经过一些代数运算后，我们得到了一个关于输入电流的、极其重要的近似表达式： \[ I_i \approx j\omega \left[ C_{gsT} + C_{gdT}(1+g_mR_L) \right] V_{gs} \] 这个结果揭示了一个惊人的现象。从输入端“看”进去，那个小小的反馈电容 \(C_{gdT}\)，其表现出的效应不再是它自身的大小，而是被放大了 \((1+g_mR_L)\) 倍！

这种现象被称为米勒效应 (Miller Effect)。其物理本质是：由于放大器（通常）是反相的，输入端 \(V_{gs}\) 的一个微小变化，会引起输出端 \(V_d\) 一个巨大的、方向相反的变化。这导致跨接在输入和输出之间的 \(C_{gdT}\) 两端承受了巨大的电压摆动。为了驱动这个巨大的电压摆动，输入信号源必须提供大得多的电流，就好像它在驱动一个被放大了的巨型电容一样。

我们可以定义米勒电容 \(C_M = C_{gdT}(1+g_mR_L)\)，那么总的输入电容就是 \(C_{in} = C_{gsT} + C_M\)。

截止频率 (\(f_T\))：晶体管的“百米冲刺”纪录

晶体管的电流增益，是有用输出电流(\(I_d = g_m V_{gs}\))与必需的输入电流(\(I_i = j\omega C_{in} V_{gs}\))之比。其大小为： \[ \left| \frac{I_d}{I_i} \right| = \frac{g_m}{\omega C_{in}} = \frac{g_m}{2\pi f (C_{gsT} + C_M)} \] 可以看到，随着频率 \(f\) 的升高，电流增益会下降。我们定义一个关键的品质因数——截止频率 (\(f_T\))，它表示电流增益下降到1（即输出电流等于输入电流，不再有放大作用）时的频率。

令增益等于1，我们可以解出 \(f_T\)： \[ f_T = \frac{g_m}{2\pi(C_{gsT} + C_M)} \] \(f_T\) 代表了晶体管能够提供任何电流增益的理论最高频率。在实际的放大器设计中，为了保证足够的增益和性能，其工作频率必须远低于 \(f_T\)。

【典型数值】

截止频率 \(f_T\) 是晶体管数据手册中的一个核心指标。对于为功率放大器设计的现代射频晶体管，根据工艺的不同，\(f_T\) 的范围很广：对于基于硅的LDMOS晶体管，其值通常在几个GHz；而对于更先进的工艺，如氮化镓(GaN)或锗化硅(SiGe)，\(f_T\) 可以轻松超过 100 GHz。拥有如此高的 \(f_T\) 是确保晶体管在其实际工作频点（例如Wi-Fi的2.4 GHz或5G的28 GHz）上依然拥有足够放大能力和良好性能的根本保障。

一个小的疑惑

晶体管的本质是一个压控电流源，输出漏极电流 \(I_d\) 的大小，是由输入栅极电压 \(V_{gs}\) 的大小来控制的。那么，既然如此，为什么我们在分析其高频性能时，却要用电流增益（输出电流 / 输入电流）来定义其截止频率 \(f_T\) 呢？

答案在于：在高频下，为了维持那个起控制作用的输入电压 \(V_{gs}\)，我们必须付出“驱动电流 \(I_i\)”的代价。

让我们把这个过程分解来看：

在直流或低频下，我们可以忽略寄生电容的影响。此时，MOSFET的栅极可以看作是断路的（输入阻抗无穷大）。 * 因 (Cause): 我们施加一个输入电压 \(V_{gs}\)。 * 果 (Effect): 晶体管忠实地在漏极产生一个输出电流 \(I_d = g_m \cdot V_{gs}\)。 * 成本 (Cost): 维持 \(V_{gs}\) 几乎不需要任何输入电流 \(I_i\)，因为栅极是绝缘的。

在这种理想情况下，讨论电流增益是没有意义的，因为输入电流几乎为零，增益会趋于无穷大。我们只关心跨导 \(g_m\)，它描述了电压到电流的转换效率。

而当频率升高时，我们再也无法忽略那个输入电容 \(C_{in}\)（由 \(C_{gsT}\) 和米勒电容 \(C_M\) 组成）。这个电容的存在，彻底改变了游戏规则。

• 因 (Cause): 我们仍然需要一个变化的交流电压 \(V_{gs}\) 来控制晶体管。
• 果 (Effect): 晶体管仍然会产生一个输出电流 \(I_d = g_m \cdot V_{gs}\)。
• 成本 (Cost): 为了让 \(V_{gs}\) 能够随高频信号快速变化，驱动它的前级电路必须提供一个输入电流 \(I_i\) 来对输入电容 \(C_{in}\) 进行反复地充电和放电。这个电流的大小为 \(I_i = j\omega C_{in} V_{gs}\)。

所以可以看到，输入电流 \(I_i\) 并不是去“控制”晶体管的，它是为了克服输入电容的阻碍，从而建立起那个真正起控制作用的 \(V_{gs}\) 所必须付出的代价。我们可以用汽车发动机来进行类比：

• 晶体管的核心 (\(g_m\)) = 汽车的发动机。发动机的输出功率（\(I_d\)）是由油门踏板的深度（\(V_{gs}\)）来控制的。这绝对是一个“位置控制功率”的系统。
• 输入电容 (\(C_{in}\)) = 油门踏板自身的弹簧和阻尼。
• 前级驱动电路 = 我们的脚。

在低频下（缓慢地踩油门），我们几乎感觉不到弹簧的力，脚只需很小的力（\(I_i\)）就能把油门踩到指定深度（\(V_{gs}\)）。

但在高频下（试图以每秒几百次的速度疯狂地点踩油门），情况完全变了！为了克服弹簧的巨大反作用力，我们的脚必须使出巨大的、快速变化的力（\(I_i\)），才能让踏板产生哪怕一点点的位移（\(V_{gs}\)）。当频率高到一定程度时，脚上花费的力（输入电流 \(I_i\)），甚至已经超过了发动机最终产生的推力（输出电流 \(I_d\)）。从整个系统的角度看，虽然我们还在“控制”，但已经“得不偿失”了。这个系统已经失去了放大的意义。

这正是我们用电流增益来定义截止频率 \(f_T\) 的原因。

所以我们不再问“这个器件是否还能被电压控制？”，而是问一个更实际的工程问题：“驱动这个器件的成本（输入电流），是否已经超过了它能带来的收益（输出电流）？”

当电流增益 \(\left| I_d / I_i \right|\) 下降到 1 时，意味着“成本”等于“收益”，这是该器件作为放大器有意义的理论极限。因此，尽管晶体管本质上是压控的，但它的高频性能瓶颈，却体现在驱动它所需要的输入电流上。我们分析电流增益，正是为了量化这个“性价比”随频率下降的趋势。

实际功放关键概念

现在，让我们走近真实的功率放大器世界，了解一些在工程实践和产品手册中经常遇到的核心概念，例如A类/B类功放、负载线、功率附加效率(PAE)等等。我们或许无法深入每一个概念的底层细节，但足以在我们已有的知识基础上，构建一个可以自圆其说的概念框架。

负载线：晶体管的“行动轨迹”

我们在生活中常听到A类、B类、AB类甚至D类放大器，它们之间最本质的区别在于晶体管静态工作点(Q点)的设置，这直接决定了晶体管在一个信号周期内的导通角度。

在对比这些功放类别之前，我们必须先理解一个至关重要的图形工具——负载线 (Load Line)。

如果说晶体管的I-V输出特性曲线（那些蓝色曲线）代表了它所有可能的工作状态，那么负载线则描绘出，在一个特定的电路中，当输入信号变化时，晶体管的工作点实际的行动轨迹。

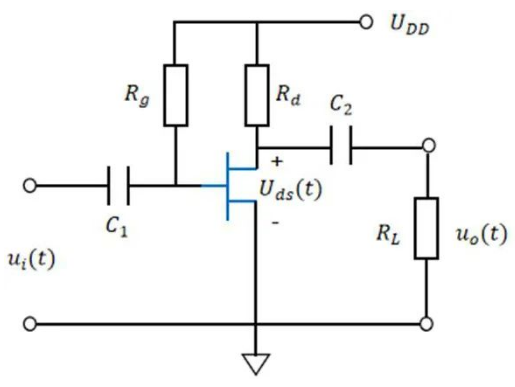
为了理解负载线，我们以一个最基础的共源极放大器为例。

完整电路	直流等效电路	交流等效电路

电路元件作用解析

这个看似复杂的电路，其每个元件都有明确的职责： * 晶体管 (MOSFET): 核心有源器件，负责放大。 * \(R_g\) 和 \(R_d\) (偏置电阻): 它们共同组成了偏置网络。其核心任务是为晶体管建立一个稳定、合适的直流静态工作点(Q点)。\(R_g\)通常很大，以确保输入信号不会被“短路”，同时为栅极提供一个确定的直流电压。\(R_d\)则将电源电压\(U_{DD}\)降低，为漏极提供一个合适的静态电压。 * \(C_1\) (输入耦合电容): 它的作用是“隔直通交”。它允许我们想要放大的交流输入信号 \(u_i(t)\) 顺利通过并进入栅极，同时阻止前级电路的直流偏置影响到我们的晶体管，也防止晶体管的直流偏置“泄露”回前级。 * \(C_2\) (输出耦合电容): 作用完全相同。它允许被放大了的交流输出信号 \(u_o(t)\) 顺利通过并传递给负载 \(R_L\)，同时阻止电源的高压直流 \(U_{DD}\) 直接“烧毁”负载。 * \(R_L\) (负载电阻): 代表放大器需要驱动的对象，例如天线、扬声器或其他电路级。

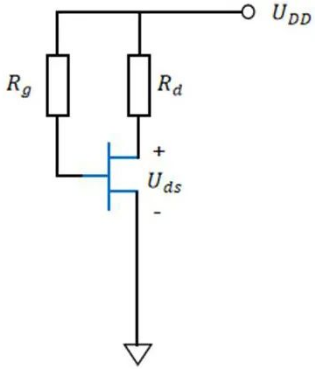
直流负载线 (DC Load Line)

首先，我们分析电路的直流状态，即没有交流信号输入时的情况。根据我们之前学到的电路等效法则（电容开路），我们可以得到上图中间的直流等效电路。

在漏极回路中，根据基尔霍夫电压定律(KVL)，我们可以写出： \[ U_{DD} = I_d R_d + U_{ds} \] 整理后得到漏极电流 \(I_d\) 与漏源电压 \(U_{ds}\) 之间的关系： \[ I_d = -\frac{1}{R_d} U_{ds} + \frac{U_{DD}}{R_d} \] 这就是直流负载线方程。它描述了在这个电路中，所有可能的直流工作点(\(I_d\), \(U_{ds}\))的集合。在晶体管的输出特性图上，这是一条斜率为 \(-1/R_d\) 的直线。

这条直线与由偏置网络决定的某条栅压曲线的交点，就是这个放大器的静态工作点Q点。

交流负载线 (AC Load Line)

接下来，我们分析电路的交流动态。当一个交流信号 \(u_i(t)\) 输入后，晶体管的栅压会在Q点上下摆动，其漏极电流和电压也会随之在Q点附近波动。

根据交流等效法则（电容短路、直流电源接地），我们得到上图右侧的交流等效电路。从晶体管的漏极看出去，交流信号的“负载”是\(R_d\) 和 \(R_L\) 的并联。我们令 \(R'_L = R_d \parallel R_L\)。

信号的总电压和总电流，是直流静态值与交流变化量的叠加： * \(I_d(t) = I_{dQ} + i_d(t)\) * \(U_{ds}(t) = U_{dsQ} + u_{ds}(t)\)

在交流通路上，输出端的交流电压变化量 \(u_{ds}(t)\) 与交流电流变化量 \(i_d(t)\) 的关系遵循欧姆定律： \[ u_{ds}(t) = -i_d(t) R'_L \] （负号表示电流增大时，电压降增大，漏极电压反而减小）

将这个关系代入到总电压和总电流的表达式中，我们可以得到交流负载线的方程： \[ I_d(t) = -\frac{1}{R'_L} U_{ds}(t) + \left(I_{dQ} + \frac{U_{dsQ}}{R'_L}\right) \] 这也是一个直线方程，其斜率为 \(-1/R'_L\)。

将两条负载线画在同一张图上，我们会得到上图的结果：

• 直流负载线（黑色）决定了静态工作点Q的位置。
• 交流负载线（紫色）穿过同一点Q，但由于并联负载 \(R'_L\) 通常小于 \(R_d\)，其斜率通常更陡。
• 这条紫色的交流负载线，才是晶体管在实际放大信号时的“行动轨迹”。当输入信号使栅压在Q点上下摆动时，晶体管的(\(I_d\), \(U_{ds}\))点就会沿着这条交流负载线来回滑动。

理解了负载线，我们就有了一张“地图”。接下来，通过在这张地图上设定不同的“起点”（Q点），我们就能够定义出不同类别的放大器，并分析它们的性能和效率。

A类、B类、C类、AB类功放：效率与线性的权衡

A类放大	B类放大

AB类放大	C类放大

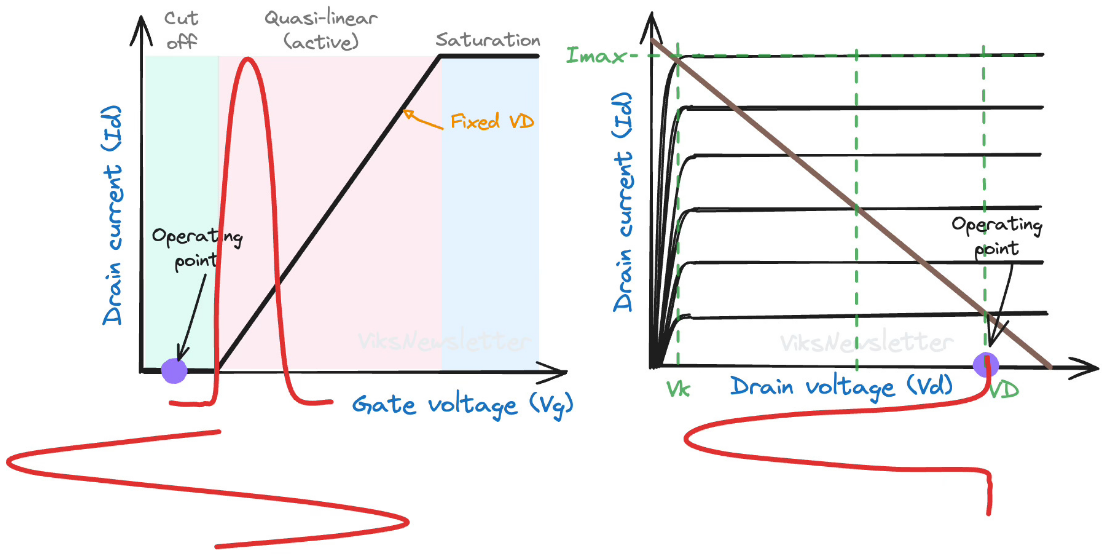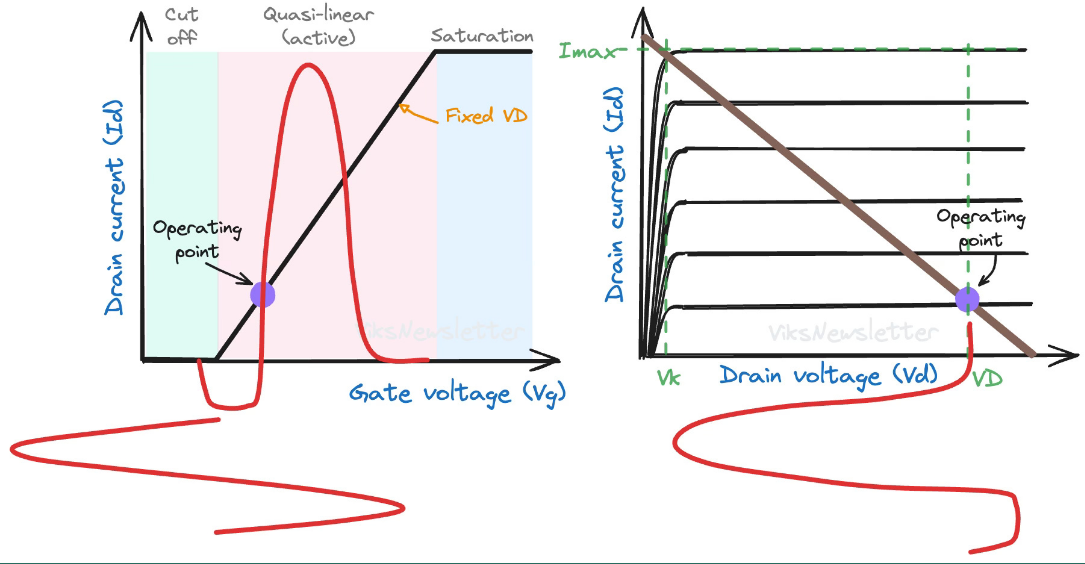
当我们理解了负载线的概念后，就能瞬间掌握不同类别放大器的核心区别——它们本质上只是静态工作点(Q点)的设置不同。这个看似简单的差异，却导致了它们在性能上巨大的权衡取舍，主要体现在效率和线性度这两个关键指标上。

A类 (Class A): 最高保真度的“常明灯”

• 负载点 (Q点): 设置在直流负载线的正中央。这意味着晶体管被偏置在一个相当大的静态直流电流 \(I_{DQ}\) 上。
• 导通角: 360°。由于Q点远离截止区，无论输入信号处于周期的哪个位置（波峰或波谷），晶体管都始终处于导通状态，忠实地放大整个波形。
• 线性度: 最佳。因为晶体管始终工作在其转移特性曲线中最陡峭、最接近线性的部分，所以输出信号是输入信号的一个几乎完美的、高保真度的放大复制品。
• 理论最高效率: 50%。这是A类功放最大的缺点。

A类功放的效率为何如此之低？

其根源在于它的“常明灯”工作模式。为了保证线性度，晶体管即使在没有信号输入时，也必须维持一个很大的静态电流 \(I_{DQ}\)。这意味着直流电源 \(P_{dc} = V_{DD} \cdot I_{DQ}\) 始终在消耗着巨大的功率。这部分功率在没有信号时，会全部转化为热量。当有信号时，一部分直流功率被转换为射频输出功率，但静态功耗的“基础开销”依然存在。因此，即使在最理想的情况下，也有一半的电能被晶体管自身消耗掉了。

B类 (Class B): “按需工作”的节能模式

• 负载点 (Q点): 精确地设置在晶体管的截止点上 (\(V_{GSQ} = V_T\)) 。静态直流电流 \(I_{DQ}\) 几乎为零。
• 导通角: 180°。晶体管只有在输入信号的正半周期（或负半周期，取决于器件类型）才会被“唤醒”并导通工作，另外一半时间则完全关闭。
• 线性度: 差。由于它只放大了信号的一半，输出波形是严重失真的。因此，单个B类放大器无法用于需要高保真度的场合。通常需要两个B类管组成推挽(Push-Pull)电路，一个负责正半周，一个负责负半周，最后再合二为一。
• 理论最高效率: 78.5%。因为没有了巨大的静态功耗，B类功放只在有信号时才从电源“按需取电”，效率得到了质的飞跃。

AB类 (Class AB): “两全其美”的黄金分割点

• 负载点 (Q点): 设置在A类和B类之间，略高于截止点。这使得晶体管有一个很小的静态电流流过。
• 导通角: 大于180°。
• 线性度: 良好。这个微小的静态电流，完美地解决了B类推挽电路在正负半周交接时产生的“交越失真”，使得线性度远好于B类，非常接近A类。
• 理论最高效率: 介于A类和B类之间，通常在 50% 到 78.5% 之间。

AB类功放是工程上最成功的折衷方案，它以牺牲少量效率为代价，换来了接近A类的优秀线性度。因此，它成为了高保真音频功放和大多数现代无线通信发射机中的绝对主力。

C类 (Class C): “脉冲式”工作的效率冠军

• 负载点 (Q点): 设置在截止点以下，即深度截止区。
• 导通角: 远小于180°。只有在输入信号的波峰最顶端，才能短暂地“踹开”晶体管的门让它导通一下，其余时间都处于深度关闭状态。
• 线性度: 极差。输出的不再是放大的信号，而是一连串与信号峰值对应的窄脉冲，原始波形信息被完全破坏。
• 理论最高效率: 非常高，可以超过90%，接近100%。因为晶体管只在极短的时间内导通，且通常在导通时其两端电压很低，瞬时功耗极小。

C类功放的极端非线性使其无法用于AM这类幅度调制的信号，但它在恒包络调制（如FM）的射频发射机中非常有用。其输出的电流脉冲可以用来激励一个LC谐振回路（“储能”电路），使其产生持续、稳定的高功率正弦波。

核心性能指标总结

• 漏极效率 (Drain Efficiency, η_D): 这是最基本的效率指标，衡量直流功率转换为射频输出功率的能力。 \[ \eta_D = \frac{P_{out, RF}}{P_{in, DC}} \]

• 功率附加效率 (Power Added Efficiency, PAE): 这是一个更“诚实”的效率指标，因为它考虑到了驱动这个功放本身也需要消耗功率。它衡量的是直流功率转换为“新增”射频功率的能力。 \[ PAE = \frac{P_{out, RF} - P_{in, RF}}{P_{in, DC}} \] 对于一个增益很高的功放，\(P_{in, RF}\) 相对于 \(P_{out, RF}\) 可以忽略不计，此时PAE约等于漏极效率。但对于增益较低的功放级，PAE能更准确地反映其真实的能量转换性能。在器件研发领域，PAE是衡量晶体管性能的黄金标准。

功放类别	静态工作点 (Q点)	导通角	线性度	理论最高效率	核心特点
A类	负载线中心	360°	极佳	50%	最高保真度，功耗巨大，发热严重
B类	截止点	180°	差	78.5%	效率高，但有交越失真，需推挽工作
AB类	高于截止点	> 180°	良好	~60-70%	效率和线性度的最佳折衷，应用最广
C类	深度截止	< 180°	极差	> 90%	最高效率，仅适用于恒包络信号

总结：信息与能量的交响曲

从最基本的通信需求出发，我们一同完成了一段跨越信息理论与物理现实的奇妙旅程。我们不仅探索了电磁波的奥秘，学习了如何通过“调制”让它开口说话，理解了“带宽”这条信息高速公路的宽度；我们更深入到了射频系统的“引擎室”，剖析了将微弱信号注入澎湃动力的核心——功率放大器。

在这段旅程的终点，让我们再次回到这篇博客的标题：信息与能量。这不仅仅是两个独立的词，它们是射频工程中相辅相成、缺一不可的两个主角，共同谱写了一曲壮丽的交响曲。

第一乐章：信息的智慧

这是关于“说什么”和“如何说清楚”的艺术。 * 我们用调制技术，将人类的语言、数据和图像，巧妙地编码到高频载波的形态变化之中。这是信息的“编码”过程。 * 我们用带宽的概念，来度量承载这些信息所必需的频谱“空间”。带宽越大，我们能传递的信息就越复杂、越迅速。这是信息的“传输”通道。 * 我们追求信号的完整性与线性度，确保经过放大和传输后，信息不会失真，接收方能准确无误地理解我们想要表达的内容。

信息的处理，是射身频系统的“大脑”和“神经”，它体现了整个系统的智慧与精密。

第二乐章：能量的肌肉

这是关于“如何说得响”和“如何传得远”的物理。 * 我们通过功率放大器(PA)，将来自直流电源的“蛮力”——直流电能，高效地转换为射频信号的能量。这是能量的“转换”过程。 * 我们通过阻抗匹配，确保能量在从功放到天线的传递过程中损耗最小，如同铺设一条没有障碍的能量高速公路。这是能量的“传输”保障。 * 我们关注效率(PAE)、增益和散热，确保在获得巨大输出功率的同时，尽可能地节约能源、避免过热。

能量的处理，是射频系统的“心脏”和“肌肉”，它体现了整个系统的力量与耐力。

尾声：一曲和谐的杰作

一个成功的射频系统，正是一曲信息与能量的完美交响。

空有巨大的能量，却承载着失真、混乱的信息，如同一个巨人语无伦次地嘶吼，毫无意义；反之，拥有完美编码的信息，却因为能量微弱而无法传达到目的地，则如同一位智者在无人山谷中喃喃自语，无人能闻。

我们今天所做的一切——从理解麦克斯韦方程组的宇宙法则，到分析晶体管的非线性脾气，再到绘制负载线这条“行动轨迹”——所有这些工具和知识，最终都是为了同一个目标：在物理定律的约束下，以尽可能高效的方式，将尽可能多的、清晰无误的信息，传递到尽可能远的地方。

我们仅仅是推开了射频世界的大门。门后还有更广阔的风景：不同功放类别（A, B, AB, D...）的效率与线性度权衡、史密斯圆图的巧妙运用、噪声与干扰的对抗、滤波器与混频器的精巧设计……

希望这篇博客能成为你探索这个迷人领域的坚实起点。当你下一次连接Wi-Fi、拨打电话或看到遥远星系的探测图像时，愿你能会心一笑，因为你已经听懂了那曲在空中回响的、关于信息与能量的壮丽交响。

部分参考

1. ABCs of Power Amplifier Classes: Class A——Design, operation and characteristics of the most linear amplifier class of all.
2. ABCs of Power Amplifier Classes: Class B——Trading off amplifier linearity for better efficiency, why harmonic traps are needed, how push-pull architecture is used for broadband circuits, and the difficulties of its implementation at RF.
3. ABCs of Power Amplifier Classes: Class AB and C——How operating in Class AB can overcome cross-over distortion in Class B push-pull amplifiers, getting near 100% efficiency in Class C, and understanding design tradeoffs in Classes A, B, AB, and C.
4. https://www.eet-china.com/mp/a125846.html
5. https://www.datatec.eu/wiki/grundlagen-der-netzwerkanalyse
6. https://coppermountaintech.com/help-r/smith-chart-format.html