器件可靠性检验基础
器件可靠性检验基础
可靠性是指一个组件或者系统在规定的工作条件下,在一定时间内能够正常工作的概率。在描述器件的可靠性时,失效率(Failure Rate,\(\lambda\))是一个最经常用到的概念,描述器件失效率的单位是FIT(Failure in Time),定义是在\(10^9\, \text{h}\)内,器件出现一次失效即为1 FIT。如果某个器件的失效率是100 FITs,那么平均预期它可以顺利工作\(10^7\, \text{h}\)。假如测试某批次的器件,被测器件有4000个,在工作\(5000\,\text{h}\)后失效了两个,那么该批次器件的失效率就是 \[ \lambda = \frac{2}{4000\times 5000\,\text{h}} = 10^{-7}\,\text{h} = 100\,\text{FITs} \]
即 \[
\lambda = \frac{r}{\text{TDH}}
\] \(r\)是测试器件失效数目,TDH(Total Device Time)是器件的总测试时间,定义为测试器件的数目乘上每个器件的测试时间。像Matthiessen定则一样,当存在多种失效机制且他们之间相互独立的时候,他们引起的失效概率是可以叠加的,此时总的失效率可以写成 \[
\lambda_t = \sum_{i=1}^{\beta}\left(\frac{r_i}{\text{TDH}}\right)\cdot \frac{\Chi^2(\alpha, \nu)}{2\sum_{i=1}^\beta r_i}
\] 其中\(\Chi^2(\alpha, \nu)\)为卡方临界值(chi-square distribution),\(\alpha\)为置信度,\(\nu\)为自由度,在可靠性计算中取\(\nu = 2\sum_{i=1}^\beta r_i + 2\),在Python里可以用scipy.stats.chi2.ppf(CL, DF)来计算,这个涉及统计的部分以后单独拿出来再看看..
实际的器件在正常工作条件下,可能要工作几百万个小时才失效,在进行可靠性测试的时候不可能等待这么长时间,那么应该如何预测它在正常工作条件下的失效时间呢?可靠性测试的核心基础是Arrhenius High Temperature Operating Life(HTOL)model,阿伦尼乌斯模型描述了在某一单一失效机制下器件寿命随温度的变化, \[ \text{TTF} = C e^{\frac{E_a}{kT}} \] 其中TTF(Time To Failure)为器件失效时间,它的倒数就代表着失效率(和弛豫时间和散射率一样),\(E_a\)为对应失效机制的表观活化能,一般认为在温度变化不太大的情况下它是一个常数。\(k\)是玻尔兹曼常数,\(T\)一般指是失效发生位置处的温度,在电子器件中,大部分情况下这个温度就选取为采用有限元仿真出的器件沟道处的温度。这个模型告诉我们,器件的寿命随着温度增加而指数衰减,所以我们可以进行加速高温寿命测试,在高温下进行器件的寿命测试,这个寿命测试就会快很多了。所以我们管这类可靠性测试叫作加速寿命测试(ALT,Accelerated Life Test)。我们定义正常条件下器件失效时间和高温测试下器件失效时间的比值为加速因子(Acceleration Factor)\(A_f\),以把前面的未知的系数\(C\)消掉, \[ A_f = \frac{\text{TTF}_\text{use}}{\text{TTF}_\text{test}} = \exp(\frac{E_a}{k}\left[\frac{1}{T_\text{use}} - \frac{1}{T_\text{test}}\right]) \] 于是当我们在测试实验中获得了高温下的失效时间后,直接把它乘上加速因子,就可以得到预测的实际使用时的器件寿命了。
不同类别失效机制的活化能一般都有一个范围,但是对应不同的器件这个数值可能不同,在实际条件下我们怎么测定呢?我们可以测量几个不同温度下的失效时间,拟合出一条器件寿命随温度变化的曲线,就可以把活化能确定下来了。最粗糙的,我们可以只测两个温度下的寿命, \[
\begin{aligned}
\ln\left(\text{TTF}_1\right) &= C + \frac{E_a}{kT_1} \\
\ln\left(\text{TTF}_2\right) &= C + \frac{E_a}{kT_2}
\end{aligned}
\] 把他们做差,就可以确定\(E_a\)了, \[
E_a = k \times \frac{\ln\left(\text{TTF}_1\right) - \ln\left(\text{TTF}_2\right)}{\frac{1}{T_1} - \frac{1}{T_2}}
\] 
一个例子
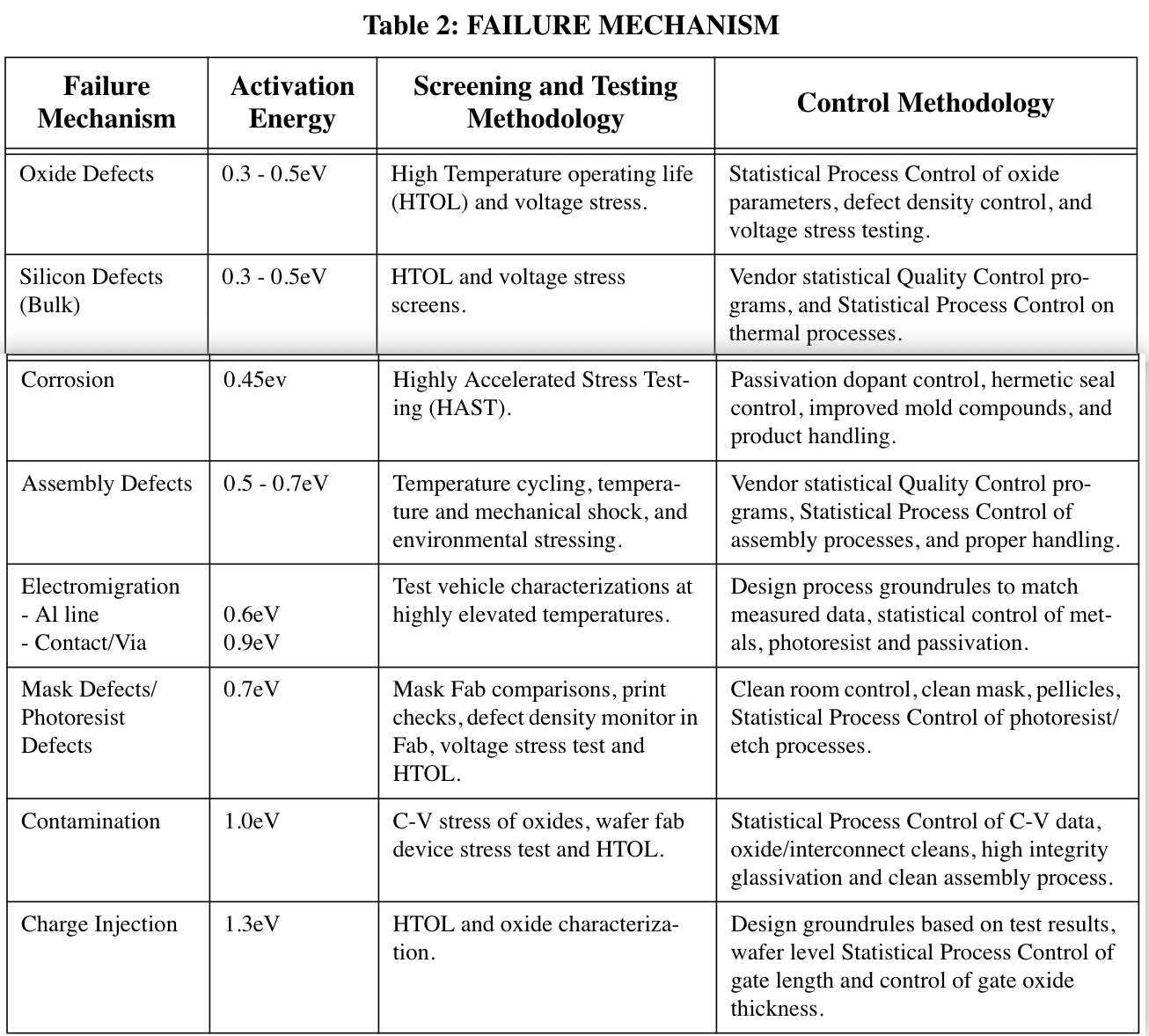
假设现在对600个器件在环境温度为150 °C的条件下测试了3000个小时,其中1个因为photoresist flaw(0.7 eV)在2000h时失效了,2个因为oxide defect(0.3 eV)在3000h时失效了。根据器件内部的热阻以及器件的运行功率,我们已经知道了器件相对环境的温升为20 °C。我们想要在置信度为60%的情况下预测器件在环境温度为55 °C条件下的寿命。首先我们可以分别计算两种失效机制对应的加速因子, \[ \begin{aligned} A F_1&=\exp \left[\frac{0.7}{8.63 \times 10^{-5}}\left(\frac{1}{273 + 55 + 20} - \frac{1}{273 + 150 + 20}\right)\right]=148.2 \quad \text{Photoresist flaw}\\ A F_2&=\exp \left[\frac{0.3}{8.63 \times 10^{-5}}\left(\frac{1}{273 + 55 + 20} - \frac{1}{273 + 150 + 20}\right)\right]=8.52 \quad \text{Oxide defect} \end{aligned} \] 这600个器件在测试中的总运行时间为, \[ \text{TDH} = 600\times 2000 + 599\times 1000 = 1.799\times10^6 \,\text{h} \] 于是这两种机制在55 °C条件下的失效率分别为 \[ \lambda_1 = \frac{1}{\text{TDH}\cdot A_{f, 1}} = 4\,\text{FITs} , \lambda_2 = \frac{2}{\text{TDH}\cdot A_{f, 2}} = 130\,\text{FITs} \] \(\alpha=0.6, \nu=2\times3 + 2 = 8\),于是得到\(\Chi^2 = 8.35\),预测器件在55 °C时的失效率为, \[ \lambda = (\lambda_1 + \lambda_2)\times \frac{\Chi^2}{3}= 373 \, \text{FITs} \]
Reference
William J. Vigrass, Calculation of Semiconductor Failure Rates
Mircosemi, Calculating Reliability using FIT & MTTF:Arrhenius HTOL Model
英飞凌, 工程师术语扫盲:如何理解FIT和MTBF?