声子水动力学+TDTR

Xiang, Z., Jiang, P., & Yang, R. (2022). Time-domain thermoreflectance (TDTR) data analysis using phonon hydrodynamic model. Journal of Applied Physics, 132(20), 205104.

杨荣贵老师刚刚发表在JAP上的一篇文章，这个文章主要的意思就是说，TDTR的热源尺寸很小，和声子的自由程相当，这会导致声子的准弹道输运，采用扩散定律分析实验结果会低估材料的热导率。这个文章用声子水动力学模型去分析TDTR测量出来的硅在80~300 K的结果，发现和稳态方法测出来的热导率吻合很好。

理论分析

TDTR用飞秒激光照射样品表面的金属薄膜，使薄膜吸收能量并将其转化为热传导给样品。金属薄膜表面温度随时间回落，从而影响到其反射率。再通过测量另一束探测激光的反射强度曲线，通过后续一系列的解调分析，得到金属薄膜温度随时间的变化，进而获得被测样品的导热特性和相关热物性参数等。

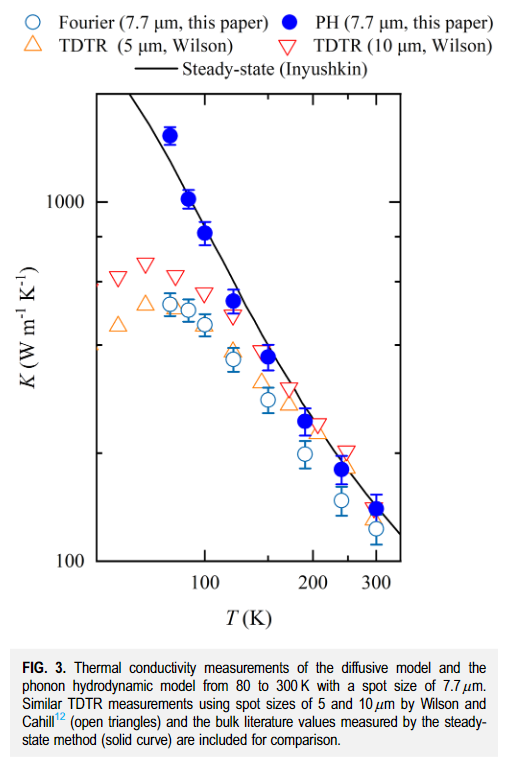
在TDTR里，所说的更改传热模型指的是更改待测样品的传热模型，而上方金属薄膜的控制方程都是用傅里叶定律计算的，所以TDTR的热信号都能整理成 \[ \Delta \Theta(\omega)=\delta\left(\omega-\omega_0\right) \times \sum_{n=-\infty}^{\infty} \Delta T\left(\omega_0+n \omega_s\right) e^{i n \omega_s t_d} \] 其中 \[ \Delta T(\omega)=\omega_s^2 A_0 A_1 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} H(u, v, \omega) \exp \left(-\pi^2 w_x^2 u^2\right) \exp \left(-\pi^2 \mathrm{w}_{\mathrm{y}}^2 \mathrm{v}^2\right) d u d v \] 扩散模型和水动力学模型的区别就是格林函数\(H(u,v,w)\)这一项。

在水动力学模型里，热流和温度梯度的关系满足， \[ \mathbf{q} + \tau \dot{\mathbf{q}} - \mathscr{l}^2 \left[\nabla^2 \mathbf{q} + \alpha \nabla (\nabla \Delta \mathbf{q})\right] = - \lambda \nabla T \] \(\tau\)是弛豫时间，\(\mathscr{l}\)是自由程，\(\alpha\)是某种非局域系数。界面的边界条件可以表示成 \[ T-T_{\Gamma}=-\frac{1}{2} b\left(\gamma_0^{-1}+\gamma_{0_{\Gamma}}^{-1}\right) \mathbf{q} \cdot \mathbf{n}+\gamma_0^{-1}(\beta \nabla \cdot \mathbf{q}-\nabla \mathbf{q}: \chi) \] 其中 \[ \begin{gathered} \gamma_0=\frac{v_g}{4} C, \gamma_{0_{\Gamma}}=\frac{v_{g_{\Gamma}}}{4} C_{\Gamma}, \\ \beta=\Omega^{-} \hbar \omega v_{g x} \frac{\tau}{C} \frac{\partial f^{\mathrm{eq}}}{\partial T} d \mathbf{k} \\ \chi_{i j}=\Omega^{-} \hbar \omega v_{g x} \frac{3 \tau}{C v_g^2} \frac{\partial f^{\mathrm{eq}}}{\partial T} v_{g i} v_{g j} d \mathbf{k} \end{gathered} \] 文章里的这些参数，包括比热容、群速度、弛豫时间等等，都是通过第一性数据取平均算出来的，通过拟合TDTR的数据，可以得到水动力学本构里的热导率\(\lambda\)。这个地方我还没有理解，按理说第一性都算出来\(\int Cv_gl\)了，热导率应该是直接确定的，这里又假设成\(Cv_gl\)和\(k\)没有关系，用TDTR的实验去反推这个\(k\)，总觉得这个逻辑有些奇怪，除非能用TDTR把\(Cv_gl\)这些参数都一起定下来... 如果用平均灰体的水动力学模型反演的热导率和第一性算出来的热导率对上了，我觉得可以比较一下水动力学模型和Full-dispersion BTE的结果，看看处理实际问题是不是这种简化的模型就足够了，不需要求解那么复杂的BTE。

结果与讨论

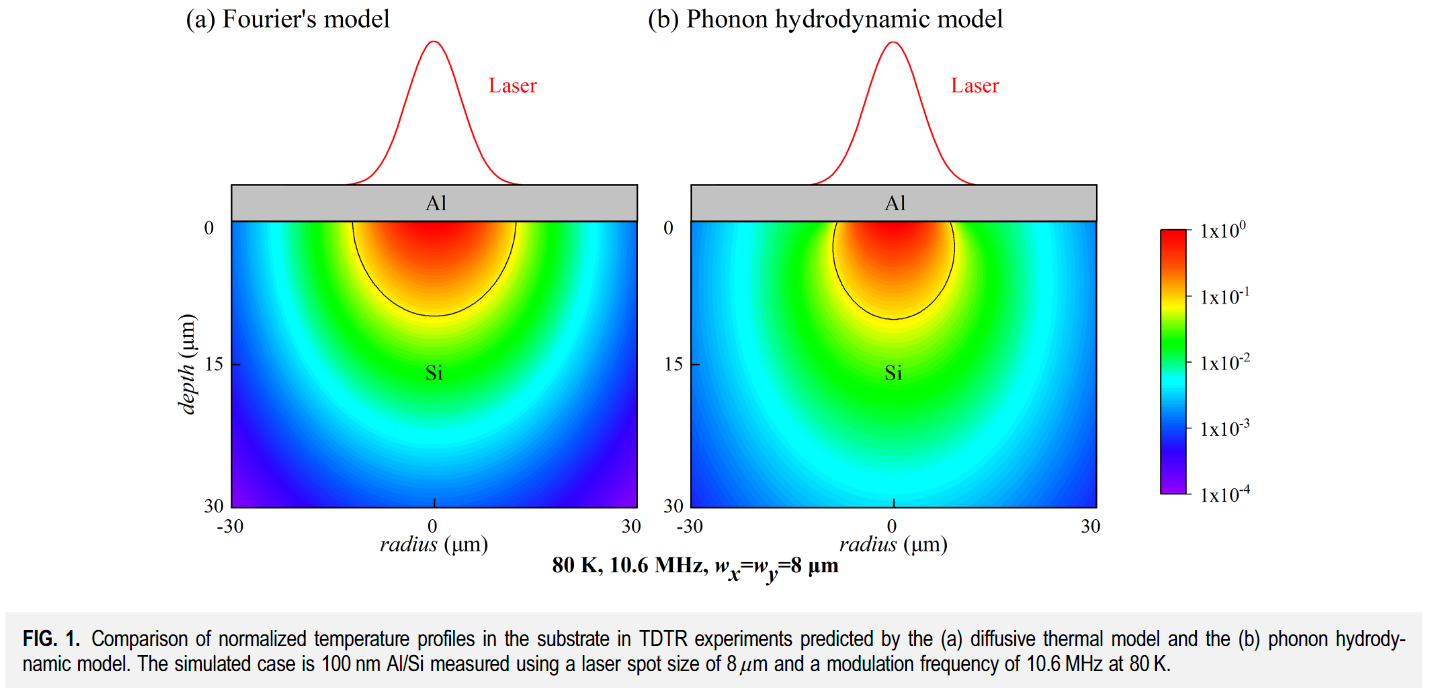
下面这个图，左右两边分别是用扩散定律和水动力学反推出来的热导率，作者发现TDTR和傅里叶都能拟合的不错，但傅里叶定律拟合出来的热导率要低很多，温度越低、声子自由程越长，低估越明显。

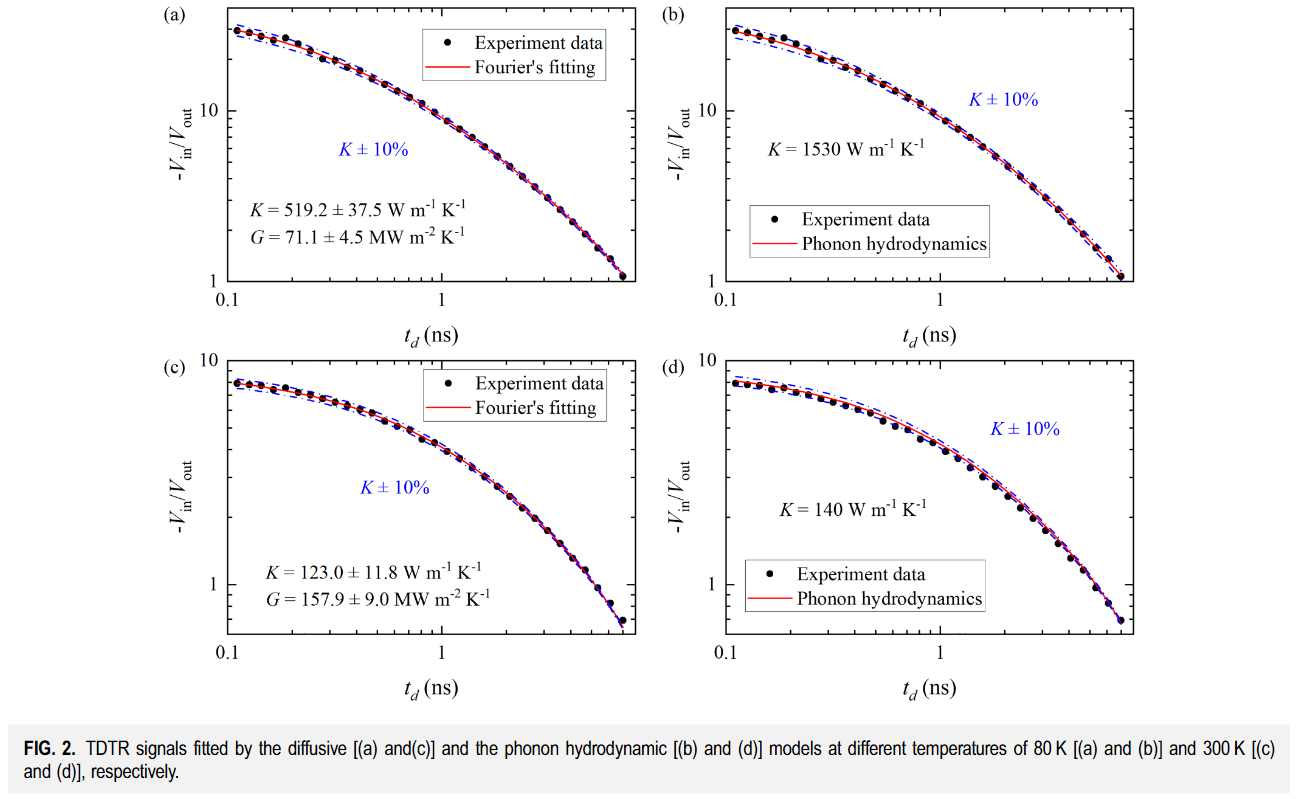
作者又测了更多的点，发现声子水动力学+TDTR可以给出和稳态方法一致的热导率，但是傅里叶定律会低估低温下的热导率，总觉得有些意犹未尽..