拟合热导率模型
拟合一个热导率模型
挤迫挤迫挤迫都市太多人
多么多么多么想变太空人

各向同性晶体假设
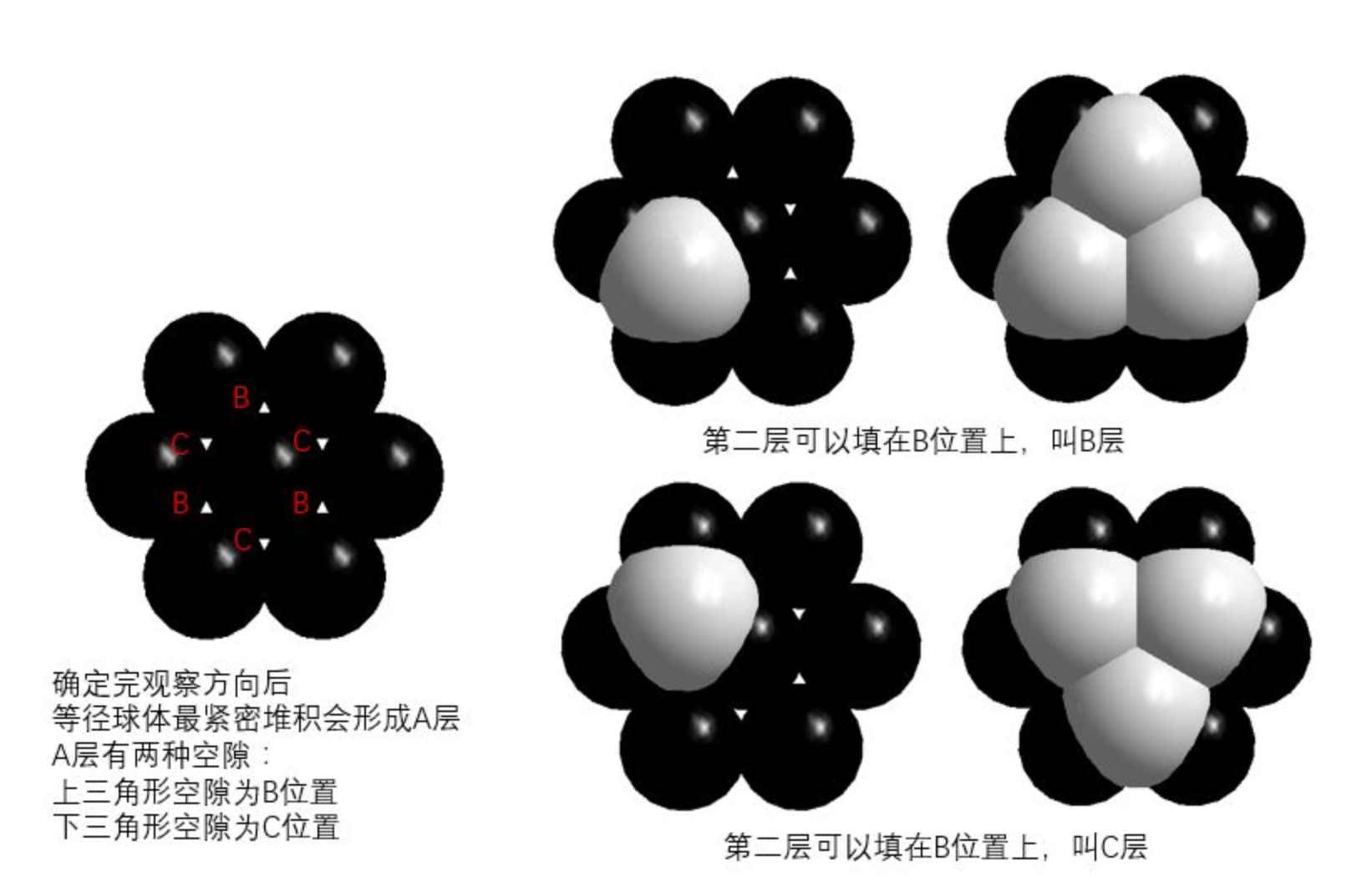
原胞
假设每个原胞含有\(p\)个原子,那么对于由\(N\)个原胞构成的晶体,总共含有\(pN\)个原子;每个原子有\(3\)个自由度,每个自由度对应于\(x,y,z\)三个方向中的一个,于是这个晶体合计有\(3pN\)个自由度。在一个布里渊区内,单一分支上允许的\(K\)值的数目恰好是\(N\)个。纵声学支和两个横声学支共有\(3N\)个模式,余下的\((3p-3)N\)个自由度属于光学支。
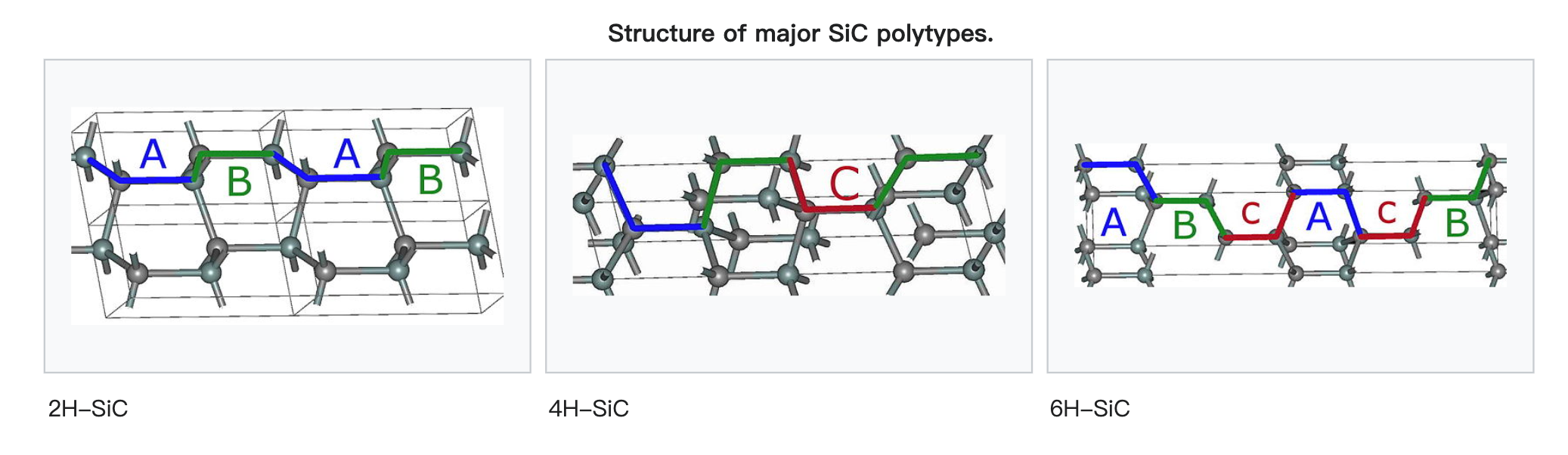
因此声学支的模式情况是取决于原胞的排布方式的,比如对于几种常见的半导体材料,纤锌矿(Wurtzite)GaN和AlN,可以看成是\(4\)个简单六方晶格嵌套而成,每个原胞内包含\(2\)对离子;金刚石结构的Si和Ge,可以看成是\(2\)个面心立方点阵的平移,虽然只由一种原子构成,但是原子位置并不是全同的,有两种位置类型的原子,因此每个原胞内包含\(2\)个原子;另外对于神奇的SiC,根据C和Si层的堆积方式的不同,存在上百种多晶(Polymorphs)(http://www.iawbs.com/portal.php?mod=view&aid=511):
2H-SiC对应的排列方式为:AB AB......
3C-SiC对应的排列方式为:ABC AB......
4H-SiC对应的排列方式为:ABAC ABAC......
6H-SiC对应的排列方式为:ABCACB ABCACB......
15R-SiC对应的ABACBCACBABCBAC型:ABACBCACBABCBAC ABACBCACBABCBAC……
SiC的命名规则是,前面数字代表一个周期性结构中包含的碳硅双原子层数,C表示立方晶系(Cubic),H表示六方晶系(Hexagonal),R表示三方晶系(Rhombohedral)。其中2H-SiC就是纤锌矿结构,一个原胞中\(2\)对SiC,4H-SiC一个原胞中包含\(4\)对SiC...
原胞的等效体积密度
可以直接用摩尔质量和晶体密度计算“化学式”组成的体积密度,然后根据晶体的类型,判断一个原胞中含有几个“化学式”,除以这个数目,即得到原胞的体积密度。声学支的模式只和原胞的分布有关,因此计算了原胞的体积密度后,后面可以进一步计算等效第一布里渊区边界的最大波矢和等效晶格常数: \[ N/V = NA\times\rho/(ZM) \]
等效最大波矢与等效晶格常数
各向同性晶体(不考虑声子支的区别)的等效最大波矢与等效晶格常数,利用总模式数来确定,这个过程和色散无关,一个量子态在波矢空间中占据的体积是固定的,因此\(3N\)个模式占据的体积也是确定的。对于各向同性晶体,若\(k_m\)为最大波矢的值,容许的模式范围在波矢空间构成了一个球: $$ \[\begin{aligned} 3\times 4/3\pi k_m^3 / (2\pi/L)^3 &= 3N \\ k_m = \left( \frac{6\pi^2N}{V} \right)^{1/3} \end{aligned}\]\[ 另外对于实际晶体来说,不同晶向上对应的第一布里渊区边界处的最大波矢都是不一样的..常见的书中推导的第一布里渊区: \] - < K $$ 是一维线型晶格的第一布里渊区,此时在第一布里渊区边界处的最大波矢就是\(\frac{\pi}{a}\)。实际上线型晶格的第一布里渊区就是一个线段。根据所研究晶体结构的不同,某一方向上最大波矢和晶格常数的关系也是不一样的。比如对于晶体Si,\((1,0,0)\)方向的\(k_m = 2\pi/a\)
对于假设的各向同性晶体,最大波矢和等效晶格常数之间的关系可以认为是和线型晶格一样的,等效晶格常数就是 \[ a = \pi / k_m \] 所以在写Dispersion类的接口的时候,不能够让晶格常数作为输入,而应该是接受所给定的第一布里渊区边界处的最大波矢为输入。
1 | import numpy as np |
结果为:
| rho | M | Z | n | k_m | a | |
|---|---|---|---|---|---|---|
| GaN | 6.15 | 85.73 | 2 | 2.16005e+28 | 1.08552e+10 | 2.89409e-10 |
| AlN | 3.255 | 40.989 | 2 | 2.39114e+28 | 1.12293e+10 | 2.79768e-10 |
| 4H-SiC | 3.21 | 40.11 | 4 | 1.20488e+28 | 8.93576e+09 | 3.51575e-10 |
关于色散和最大角频率
可以把总模式数的计算转换到频率空间的积分,观察一下实际上色散在这里起到什么作用:
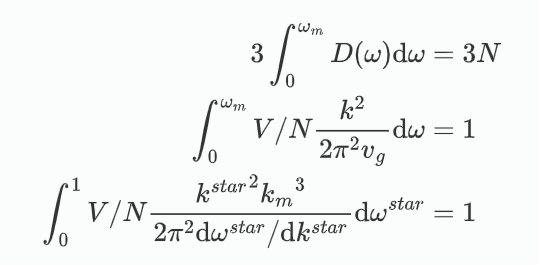
最大角频率对积分值的大小没有影响,如果这个晶体德拜晶体,没有色散,则\(\mathrm{d}\omega^{star}/\mathrm{d}k^{star}=1\),那么左侧的积分变成了:
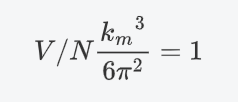
根据\(k_m\)的定义,这是自然成立的。如果假设了色散关系,即\(k^{star}\in(0,1) \rightarrow \omega^{star}\in (0,1)\)的映射,左侧的积分会略偏离于1.
最大角频率可以通过声速来确定:
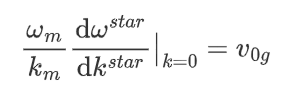
但这个低频极限的声速的选取,没有什么具体的标准,“The specification of \(v_{0g}\) is somewhat arbitrary. ”(Chung J D, McGaughey A J H, Kaviany M. Role of phonon dispersion in lattice thermal conductivity modeling[J]. J. Heat Transfer, 2004, 126(3): 376-380.),比如一个选择是: \[ \frac{1}{v_{0g}} = \frac{1}{3}\left( \frac{1}{v_{0g,L}} + \frac{2}{v_{0g,T}} \right) \] 从头到尾都是无数的近似..这里也不是什么主要矛盾了。
如果采用Sine色散模型: \[ \omega = \omega_m\sin(\pi k/2k_m) \] 那么最大色散就是 \[ \omega_m = 2v_{0g}/a \]
体材料弛豫时间模型
关于散射机制
在Gang Chen老师的书(175-176)里,给出了一些经典的弛豫时间近似表达式。
对于杂质散射,典型的声子波长处于nm量级,而一般缺陷的尺寸处于Am量级,这种情况下可以认为散射遵循Rayleigh定律 \[ \tau_i^{-1} = A\omega^4 \] \(A\)是常数,用热导率实验数据拟合得到。
对于三声子倒逆散射(U散射)过程,一个常用的近似表达式为: \[ \tau_u^{-1} = B\omega^2T\exp(-C/T) \] 其中\(B,C\)是常数,用热导率实验数据拟合得到。
可以粗糙的认为(?)体材料中重要的散射机制主要就是这两种,于是根据马森西定则,总声子弛豫时间可以表达为: \[ \tau^{-1} = A\omega^4 + B\omega^2T\exp(-C/T) \] 在给出色散模型后,可以计算理论的体材料热导率: \[ k = \int_0^{\omega_m}C(\omega)v_g^2(\omega)\tau(\omega)\mathrm{d}\omega \] 通过对实验值做拟合,可以得到\(A,B,C\)的值。但这里有很多tricky和说不清的地方,一个就是声子的自由程是随着温度的减小而增加的,在低频、极低温下(比如10K),理论上声子自由程可以达到米的量级,这时候虽然文献里的实验自称是体材料的热导率值,在极低温下,这个体材料的概念也绝对不成立了,此时用上面的弛豫时间表达式,绝对拟合不出来低温的热导率变化。
这个时候,可以认为声子会和材料的边界发生边界散射,在总弛豫时间中加上一项边界散射项,(虽然这种处理是争议的) \[
\tau_b^{-1} = v_b/FL
\] \(L\)是材料的特征尺寸,\(F\)是形状因子,\(v_b\)是平均群速度。此时要想拟合出低温区间的热导率变化,至少要加上散射项这一项常数: \[
\tau^{-1} = A\omega^4 + B\omega^2T\exp(-C/T) + D
\] 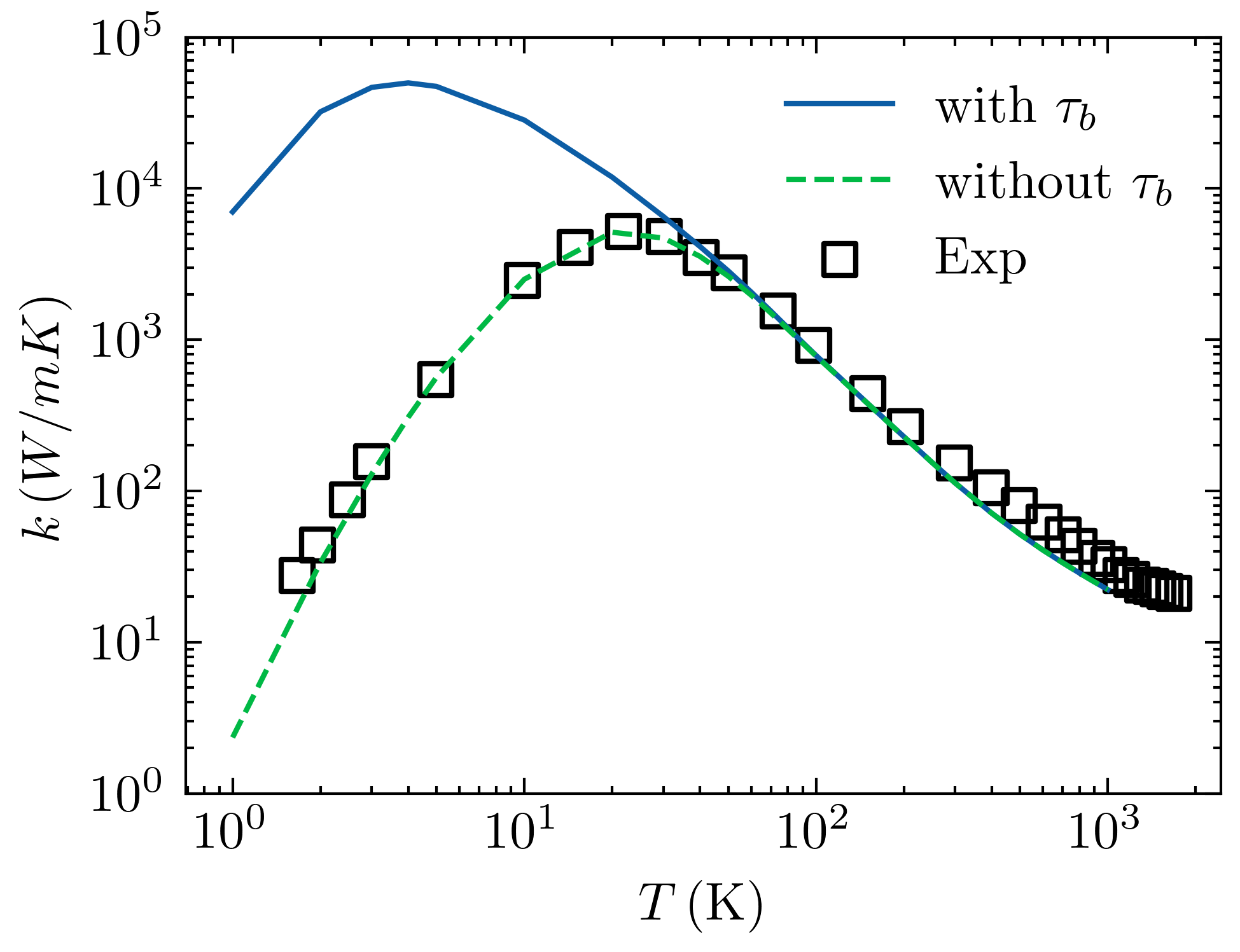
这个图是用BZBC模型(从声子色散到热导率)计算的是否考虑\(\tau_b\)下的热导率计算值,可以看到在热导率峰值温度后,\(\tau_b\)的影响基本消失,而在峰值温度前,\(\tau_b\)起到了决定性的影响。因此在拟合体材料热导率时,拟合温度起点只能从峰值温度一段后开始,前面一段是没有意义的。
另一方面,这个忽略L支和T支的区别,全部采用\(B\omega^2T\exp(-C/T)\)这种近似的弛豫时间表达式是相当粗糙的,一方面没考虑N散射的贡献,另一方面T支和L支的弛豫时间变化的区别还是存在的,Holland的文章里总结了一些弛豫时间模型({star}Holland M G. Analysis of lattice thermal conductivity[J]. Physical review, 1963, 132(6): 2461.{star})

在Callaway模型的基础上提出了经典的三部分热导率模型,把T支分成两段来考虑,T支的前半段布里渊区忽略U散射,只考虑N散射的贡献;后半段布里渊区忽略N散射,只考虑U散射的贡献;在L支中把U和N用同一个表达式来表示。

当然这个表达式应该只适用于硅、锗一类的材料,对于GaN,N散射过程只在极低温下才有贡献,对于U散射,普遍还是采用\(B\omega^2T\exp(-C/T)\)的表达式进行拟合(唐道胜, 华钰超, 周艳光, 等. GaN 薄膜的热导率模型研究[J]. 2021.)。
实际上就算对于\(Si\),忽略L支和T支的区别,用一个各向同性的统一色散模型,采用\(A,B,C\)的三参数弛豫时间表达式,也能对体材料热导率做出一个很好的近似,下面这个是用Sine色散模型拟合的Si的体材料热导率。当然这时没法分析不同声子支的贡献了,这个东西是不是valid的也需要再考虑考虑。
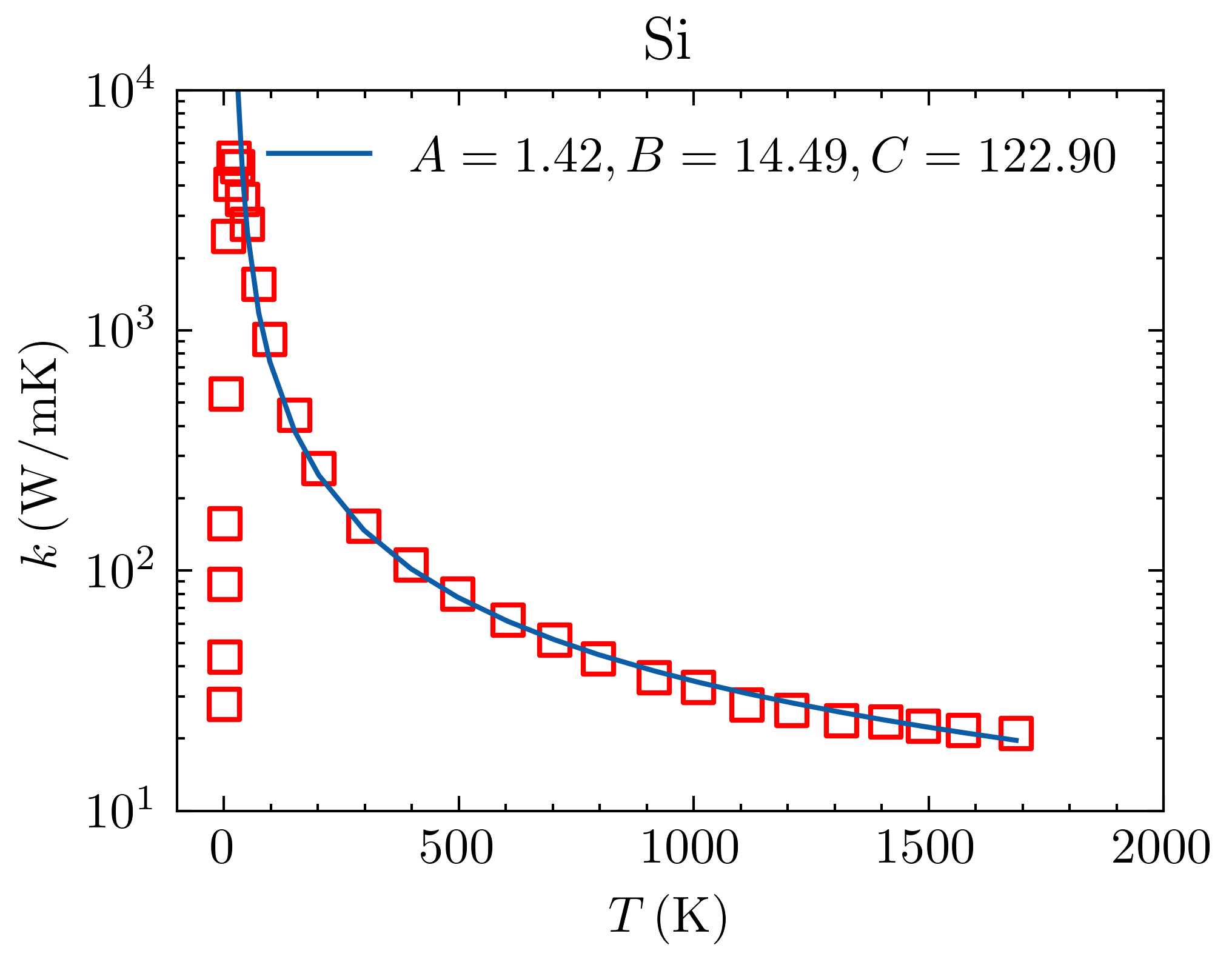
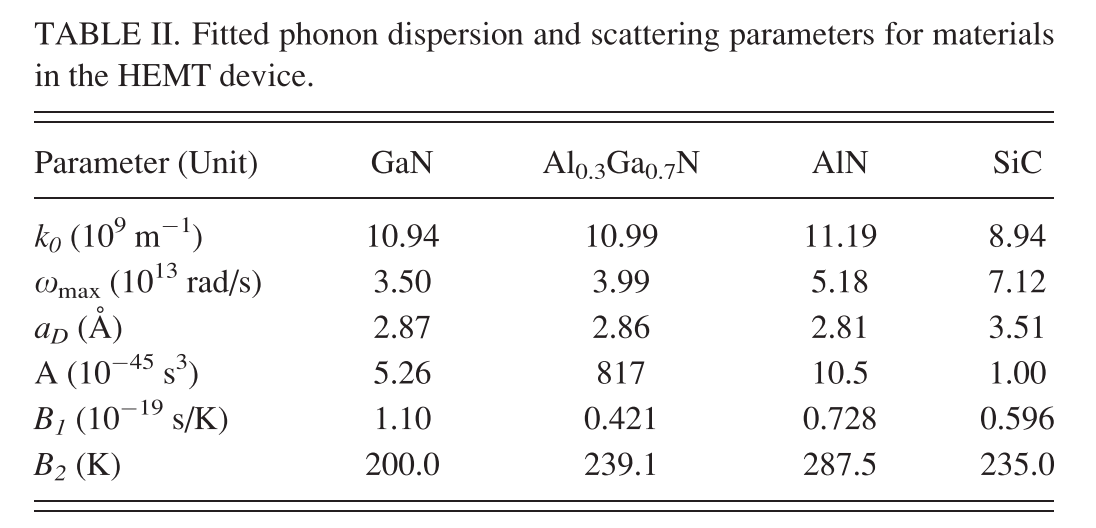
GaN和AlN的热导率模型
这是Hao Q用各向同性Sine色散模型拟合的四个材料的参数,假设三个声学支全同,只考虑U散射和impurity散射,假设这两个散射机制的弛豫时间可以用上面的的三个参数来确定(他发的有关热电mc模拟的文章里全是这几个参数)(Hao Q, Zhao H, Xiao Y. A hybrid simulation technique for electrothermal studies of two-dimensional GaN-on-SiC high electron mobility transistors[J]. Journal of Applied Physics, 2017, 121(20): 204501.)
以AlN和GaN为例,重复一下参数的拟合过程:
1 | import numpy as np |
shengmc是我写的一个in house的python based的二维mc库(虽然只有我一个人用。。),总之这里的基本逻辑就是给定实验数据experiment_T, experiment_k,优化弛豫时间模型中的\(A,B,C\)参数,这里用到了\(scipy.optimize\)里面的leastsq函数,这个函数的基本调用方式如下
1 | leastsq(error, p0, args=(x, y)) |
其中p0是猜测的要拟合的参数的初始值数组,args=(x, y)中的x, y分别是实验值的横纵坐标数组,error是自己定义的误差函数,输入应为(p, x, y),其中p是要拟合的参数数组,x为横坐标数组,y为用给定的p参数数组得到的输出值。
scipy.optimize这个模块里的函数,接口都是数组,不论是输入的p,x,y还是error函数的返回值。因此如果error函数里面调用的函数不支持数组的广播操作,必须手动将x数组循环展开,最后再返回一个数组。

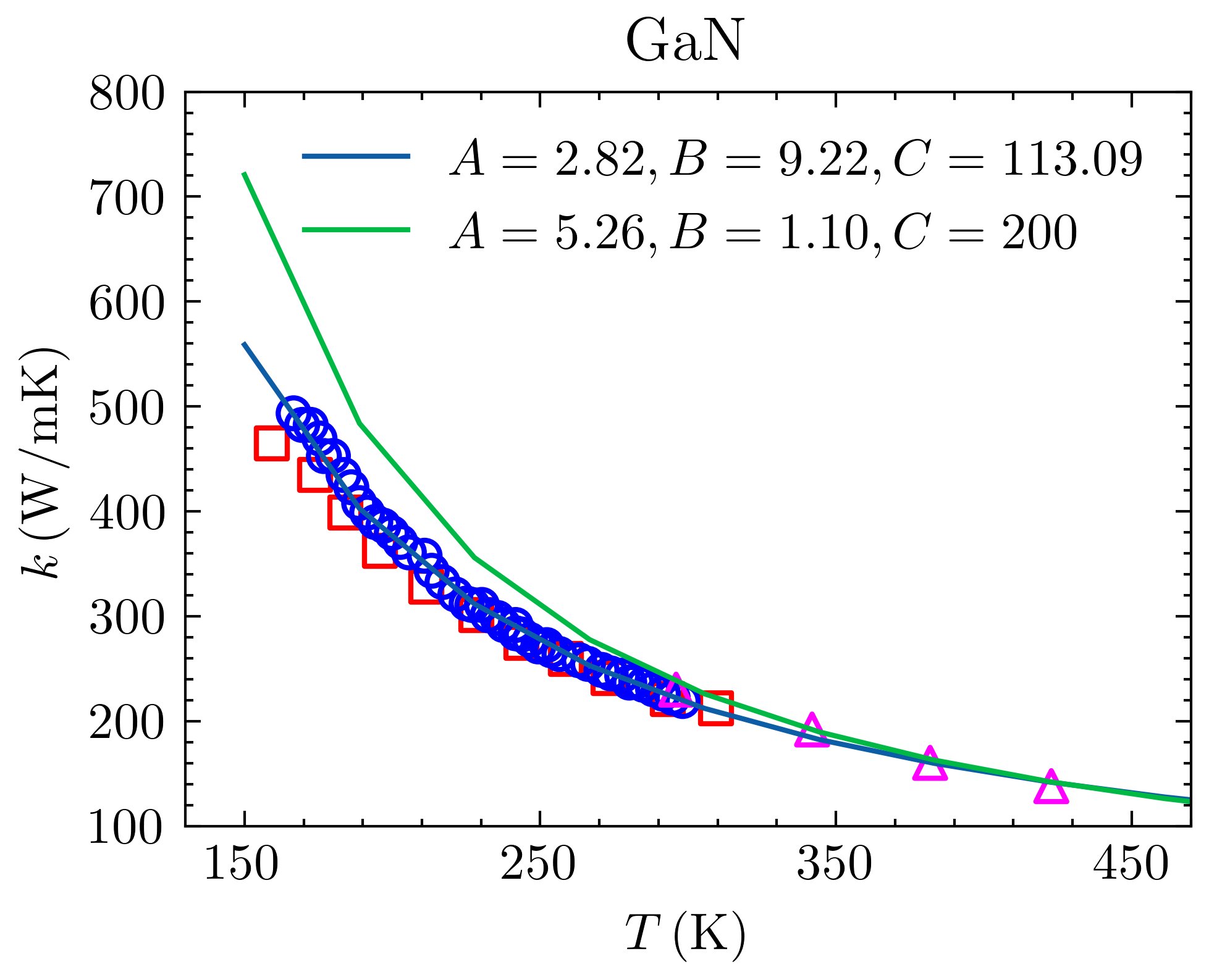
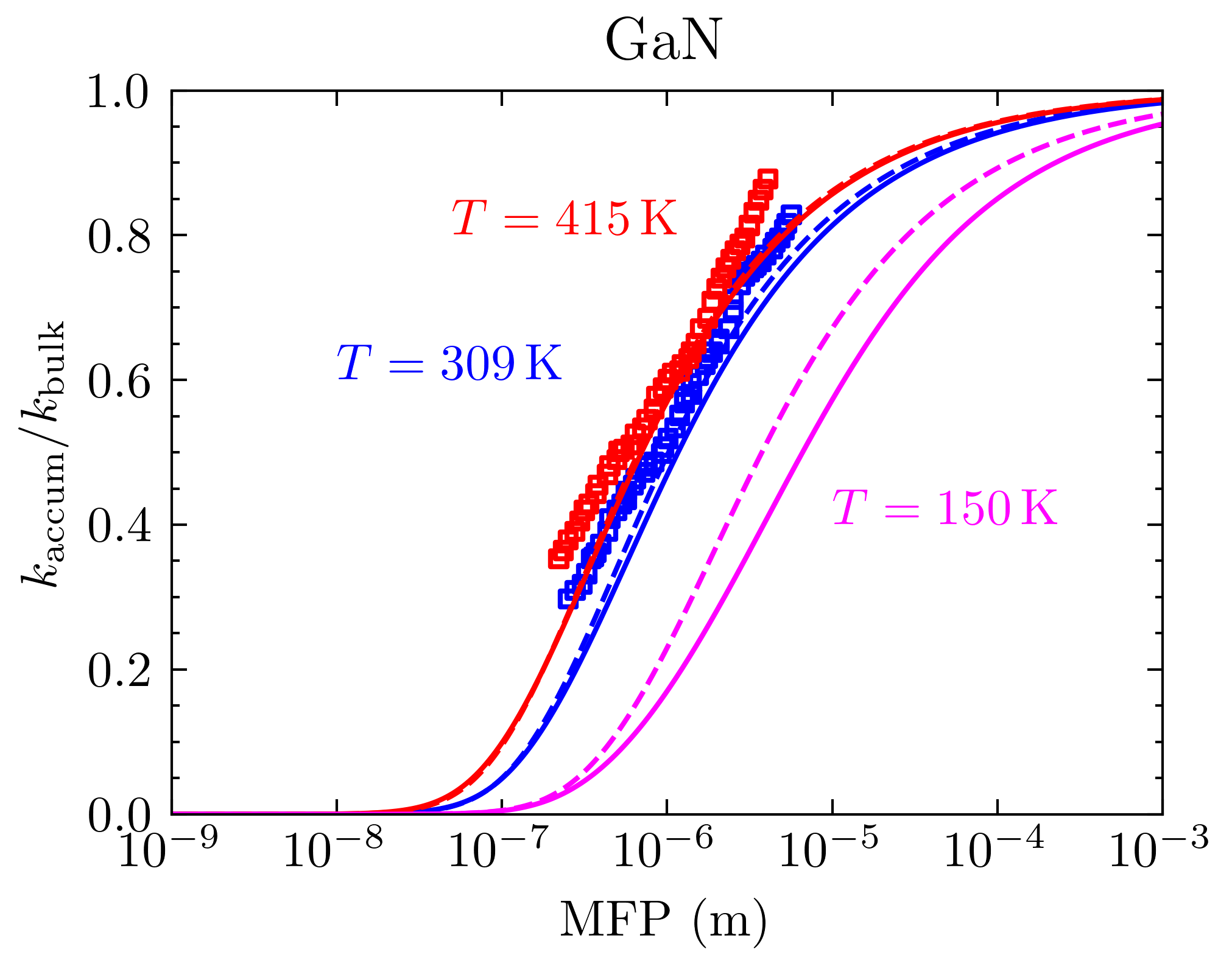
上图是优化的结果和Hao Q给的参数计算结果以及实验值的对比(Slack G A, Tanzilli R A, Pohl R O, et al. The intrinsic thermal conductivity of AIN[J]. Journal of Physics and Chemistry of Solids, 1987, 48(7): 641-647.; Danilchenko B A, Obukhov I A, Paszkiewicz T, et al. On the upper limit of thermal conductivity GaN crystals[J]. Solid state communications, 2007, 144(3-4): 114-117.),下面是热导率累积函数随平均自由程的变化,虚线是新拟合的弛豫时间,实线是Hao Q文章里的参数。可以看出来实际上在这种无数的近似下,这些参数的影响也不是决定性的了,也只能定性地反应一些问题。