格子玻尔兹曼

电热输运

格子玻尔兹曼

Create Your Own Lattice Boltzmann Simulation (With Python)

Philip Mocz

Computational Astrophysicist @Princeton

https://github.com/pmocz/latticeboltzmann-python

射线跟踪Monte Carlo和BTE的关系并不是非常直观的，刚接触的时候很难建立一些概念。但是格子玻尔兹曼（LBM）基本上就是直接离散BTE了，形式上非常直观，感觉对于复杂边界处理比Monte Carlo要容易不少

相空间

分布函数\(f(\boldsymbol{r}, \boldsymbol{p})\)是相空间中（坐标空间+动量空间）的函数，如果分析的体系是N维的，那么\(f(\boldsymbol{r}, \boldsymbol{p})\)就是一个2N维的函数。在相空间中，如果某个点的坐标确定，它仍有N个动量空间的自由度，因此这个点处某个物理量的宏观表现（只是坐标空间的函数），实际是该点处动量空间贡献之和。在相空间中，这个点向各个方向都有速度，而该点宏观体现出来的实际速度就是这些速度按照权重\(f\)叠加出来的净结果。这也是用\(f\)求分布的一般方法： \[ \langle X(\boldsymbol{r})\rangle=\ \int X(\boldsymbol{r}, \boldsymbol{v}) f(\boldsymbol{r}, \boldsymbol{v}) \mathrm{~d} \boldsymbol{v} \]

格子玻尔兹曼

基本想法

在D2Q9（2维9速度分量）格子玻尔兹曼中，空间中的每一个点都储存着9个速度分量，分别指向上下左右以及四个角点。这些速度分量就离散地代表了\(f(\boldsymbol{r}, \boldsymbol{p})\)在动量空间的分布。因此空间中的每一点原本需要计算在动量空间的积分， \[ \langle X(\boldsymbol{r})\rangle=\ \int X(\boldsymbol{r}, \boldsymbol{v}) f(\boldsymbol{r}, \boldsymbol{v}) \mathrm{~d} \boldsymbol{v} \] 现在就可以用求和代替了， \[ X(\boldsymbol{r}) = \sum_{i=1}^9 f(\boldsymbol{r}, \boldsymbol{v_i})X(\boldsymbol{r}, \boldsymbol{v_i}) = \sum_{i=1}^9 f_iX_i \] 实际上密度就是把分布函数的速度部分积分掉： \[ \rho(\boldsymbol{r}) = \sum_{i=1}^{9} f_i \] 动量可以表示为： \[ \rho(\boldsymbol{r})\boldsymbol{u}(\boldsymbol{r}) = \sum_{i=1}^{9} f_i \boldsymbol{v_i} \] 下图是D2Q9模型中空间中每一点的速度离散及其权重示意图，权重主要决定了后面平衡分布的计算，它肯定是可以推导的，不影响对方法本身的理解。

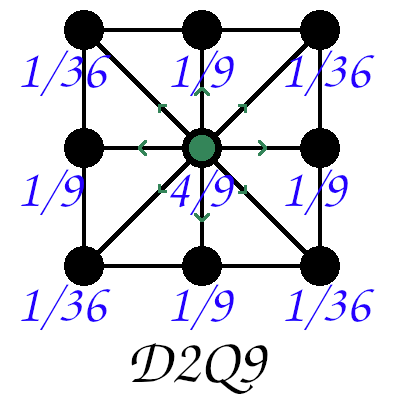
在D2Q9模型中，最终想要求解的是\(f\)在空间中的分布，在空间中的每个点都存储\(f\)的9个分量，因此如果在x方向离散了100个网格，在y方向离散了100个网格，\(f\)的数据结构就是\(100\times100\times9\)的矩阵。

演化

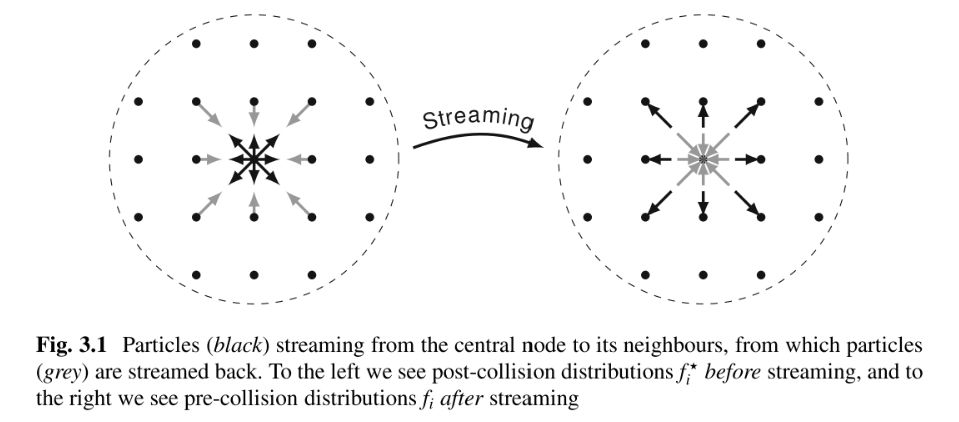
弛豫时间近似下的玻尔兹曼方程： \[ \frac{\mathrm{d}f(\boldsymbol{r}, \boldsymbol{v}, t)}{\mathrm{d}t} = -\frac{f-f^{\mathrm{eq}}}{\tau} \] 写成离散格式： \[ \frac{f(\boldsymbol{r} + \boldsymbol{v}\delta t, \boldsymbol{v} + \boldsymbol{F}\delta t, t+\delta t) - f(\boldsymbol{r}, \boldsymbol{v}, t)}{\delta t} = -\frac{f(\boldsymbol{r}, \boldsymbol{v}, t)-f^{\mathrm{eq}}(\boldsymbol{r}, \boldsymbol{v}, t)}{\tau} \] 在没有外力的情况下，可以把上面这个\(f\)的离散写成9个分量的离散： \[ \frac{f_i(\boldsymbol{r} + \boldsymbol{v_i}\delta t, t+\delta t) - f_i(\boldsymbol{r}, t)}{\delta t} = -\frac{f_i(\boldsymbol{r}, t)-f_i^{\mathrm{eq}}(\boldsymbol{r}, t)}{\tau} \] 左边的离散是一个类似拉格朗日观点的处理方式，把它叫作漂移项（drift），在下一个时间步，当前位置的九个速度格子都跑到对应速度方向的下一个格子上。将右边称作碰撞项（collision），类似欧拉的流场，只关注当地的平衡态和非平衡态。上面这个等式给出了\(f\)更新的方式，\(f\)在每一步中要经历碰撞和漂移两个过程，到达下一时间步，继续碰撞和漂移过程。

img

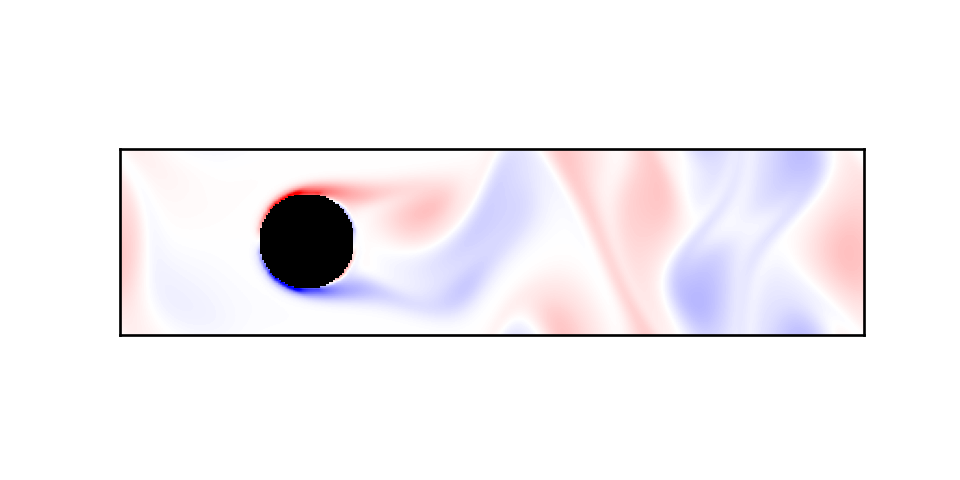
对于等温（声速不变）流体，平衡态分布可以表示为： \[ f_{i}^{e q}=w_{i} \rho\left(1+3\left(\mathbf{v}_{i} \cdot \mathbf{u}\right)+\frac{9}{2}\left(\mathbf{v}_{i} \cdot \mathbf{u}\right)^{2}+\frac{3}{2}(\mathbf{u} \cdot \mathbf{u})^{2}\right) \] 以圆柱扰流为例，流场中存在一个圆柱，在格子玻尔兹曼中，圆柱一圈的网格会收到边界的影响，可以简单认为如果粒子撞到了边界就弹回来，体现在分布函数上就是\(f_i <->f_j\)，交换对向格子。

Code

定义模拟的基本参数，x方向离散400个网格，y方向离散100个网格，平均密度设置为100，弛豫时间0.6，更新步数选取为4000个

1
2
3
4
5
6
# Simulation parameters
Nx          = 400    # resolution x-dir
Ny          = 100    # resolution y-dir
rho0        = 100    # average density
tau         = 0.6    # collision timescale
Nt          = 4000   # number of timesteps

每个点设置9个速度格子，cxs和cys是格点的横纵坐标，weights是对应点的权重

1
2
3
4
5
6
7
# Lattice speeds / weights
NL = 9
idxs = np.arange(NL)
cxs = np.array([0, 0, 1, 1, 1, 0,-1,-1,-1])
cys = np.array([0, 1, 1, 0,-1,-1,-1, 0, 1])
weights = np.array([4/9,1/9,1/36,1/9,1/36,1/9,1/36,1/9,1/36]) # sums to 1
X, Y = np.meshgrid(range(Nx), range(Ny))

F为存储分布函数的三维数组，每个点存储9个速度格子的分布。给出分布函数一个随机的扰动，同时流场的初始条件是向右的速度分布，体现在分布函数上就是每个点正右侧格子的分布函数的值要大一点，F[:,:,3]就是坐标为\((1, 1)\)的格子在全场的分布。np.sum(F, 2)代表对数组F的第三维求和。

1
2
3
4
5
6
# Initial Conditions - flow to the right with some perturbations
F = np.ones((Ny,Nx,NL)) + 0.01*np.random.randn(Ny,Nx,NL)
F[:,:,3] += 2 * (1+0.2*np.cos(2*np.pi*X/Nx*4))
rho = np.sum(F,2)
for i in idxs:
  F[:,:,i] *= rho0 / rho

定义边界：

1
2
# Cylinder boundary
cylinder = (X - Nx/4)**2 + (Y - Ny/2)**2 < (Ny/4)**2

下面就是主循环过程，首先进行漂移过程，对F进行更新，np.roll(F[:,:,i], cx, axis=1)的含义是把F[:,:,i]沿x方向滚动cx个元素，超出最后位置的元素将会滚动到第一个位置。这两句实际上执行了上边的示意图里的过程。接下来处理边界，以及碰撞过程，每一个时间步里F分别用碰撞和漂移更新一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Simulation Main Loop
for it in range(Nt):
  
  # Drift
  for i, cx, cy in zip(idxs, cxs, cys):
    F[:,:,i] = np.roll(F[:,:,i], cx, axis=1)
    F[:,:,i] = np.roll(F[:,:,i], cy, axis=0)
  
  # Set reflective boundaries
  bndryF = F[cylinder,:]
  bndryF = bndryF[:,[0,5,6,7,8,1,2,3,4]]
  
  # Calculate fluid variables
  rho = np.sum(F,2)
  ux  = np.sum(F*cxs,2) / rho
  uy  = np.sum(F*cys,2) / rho
  
  # Apply Collision
  Feq = np.zeros(F.shape)
  for i, cx, cy, w in zip(idxs, cxs, cys, weights):
    Feq[:,:,i] = rho*w* (1 + 3*(cx*ux+cy*uy) + 9*(cx*ux+cy*uy)**2/2 - 3*(ux**2+uy**2)/2)
  
  F += -(1.0/tau) * (F - Feq)
  
  # Apply boundary 
  F[cylinder,:] = bndryF