热穿透深度

读文献的时候遇到了一个热穿透深度（Thermal penetration depth）的概念，出现在Time Domain Thermoreflectance（TDTR）时域热反射测量技术中。

基本定义

一个半无限大的物体，边界条件为周期性振动的温度边界，此时在物体内部会产生振幅呈指数衰减的温度振荡分布，为了描述这种温度分布情况，定义热穿透深度 \[ L_p = \sqrt{k/C\pi f} \] 其中\(f\)​​是激光的调制频率（modulation frequency），\(k\)​​是材料的热导率，\(C\)​是材料的比热容，\(L_p\)​​表明了垂直于表面的深度，在这个深度温度振幅是它的表面振幅的\(e^{-1}\)​​。

对于平行流来说，速度只在一个方向上有分量，且在该方向上没有梯度，NS方程里的对流项为0，动量输运只有扩散过程。对于牛顿流体，控制方程就是扩散型方程，对于这类满足扩散定律的体系，（通量密度=输运系数\(\times\)梯度），比如满足菲克定律的扩散过程，满足傅里叶定律的热传导过程，控制方程都是一样的。因此实际上这个热穿透深度的求解就是Stokes第二问题的一个结果。

Stokes第二问题

Problem Statement

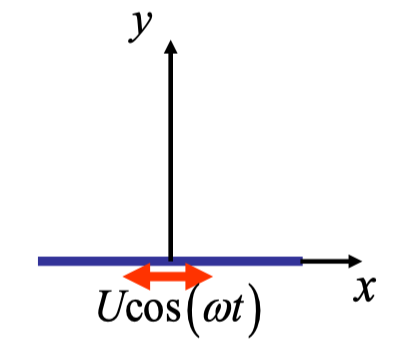
\[ \begin{aligned} \frac{\partial \theta(x,t)}{\partial t} &= \alpha \frac{\partial^2 \theta(x,t)}{\partial x} \\ \theta(0,t) &= \theta_0\mathrm{e}^{-i\omega t}\\ \theta(\infty,t) &= 0 \end{aligned} \]

分离变量法

\[ \begin{aligned} \theta(x,t) &= f(x)e^{-i\omega t} \\ \end{aligned} \]

方程变为： \[ f^{\prime\prime}(x) = \lambda^2f(x),\quad \lambda^2 = -i\omega/\alpha \] 边界条件变为： \[ f(0) = \theta_0, \quad f(\infty) = 0 \] 通解为： \[ f(x) = Ae^{\lambda x} + Be^{-\lambda x}, \quad \lambda = \sqrt{\frac{\omega}{2\alpha}}(1-i) \] 满足边界条件的解为 \[ A=0,B=\theta_0,f(x) = \theta_0e^{-\lambda x} \] 于是 \[ \theta = \theta_0e^{-\sqrt{\frac{\omega}{2\alpha}}x }e^{i(-\omega t + x\sqrt{\frac{\omega}{2\alpha}})} \]

热穿透深度

这个解是一种沿板面法向传播的横波，复指数项决定了波的相位，实指数项控制波的振幅，随着远离平面，振幅随指数衰减，衰减的程度与边界振动频率和扩散系数有关，在距离边界\(\sqrt{2\alpha/\omega}\)​的距离处，波的振幅下降为边界振幅的\(\mathrm{e}^{-1} = 0.368\)​，于是 \[ L_p = \sqrt{2\alpha/\omega} = \sqrt{\frac{2k}{C}/(2\pi f)} = \sqrt{\frac{k}{C\pi f}} \] 顺便回顾一下Stokes第一问题

Stokes第一问题

关于误差函数

\[ erf(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\mathrm{d}t \]

误差函数是热传导型方程的初边值问题的解析解。

Problem Statement

\[ \begin{aligned} \frac{\partial \theta(x,t)}{\partial t} &= \alpha \frac{\partial^2 \theta(x,t)}{\partial x} \\ \theta(x,0) &= \theta_0\\ \theta(\infty,t) &= 0 \end{aligned} \]

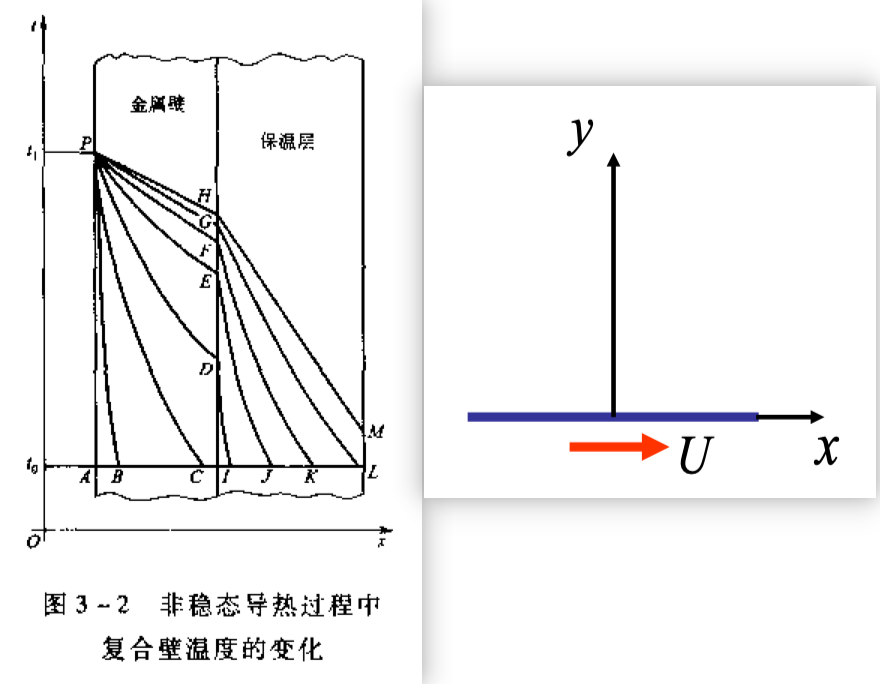
在热传导问题中，\(\theta = T - T_0\)​​为过余温度，\(\alpha = \lambda/(\rho C_p)\)​​​为热扩散系数；在Stokes第一问题中，\(\theta\)​为流体速度，\(\theta_0\)​​为突然启动的平板速度，\(\alpha=\mu/\rho\)运动粘性系数。

量纲分析

等效无量纲速度为\(x,t,\alpha\)​的函数 \[ \theta/\theta_0 = f(x,t,\alpha) \] 这三个物理量能够组成的独立的无量纲数只有一个： \[ \eta = \frac{x}{2\sqrt{\alpha t}} \] 于是根据白金汉\(\pi\)定理 \[ \theta / \theta_0 = f(\eta) \] 利用复合函数的微分法则： \[ \begin{aligned} \frac{\partial \theta}{\partial t} &= \theta_0 \frac{\partial f(\eta)}{\partial \eta}\frac{\partial\eta}{\partial t} = - \frac{\eta}{2t}\theta_0f^\prime \\ \frac{\partial \theta}{\partial x} &= \theta_0 \frac{\partial f(\eta)}{\partial \eta}\frac{\partial\eta}{\partial x} = \frac{1}{2\sqrt{\alpha t}}\theta_0f^\prime \\ \end{aligned} \] 带回原方程可得到： \[ \begin{array}{l} f^{\prime\prime} + 2\eta f^{\prime} = 0 \\ f(0) = 1, f(\infty) = 0 \end{array} \] 积分得到： \[ f^{\prime} = A\exp(-\eta^2) \] 再次积分得到： \[ f(\eta) = 1 + A \int_0^\eta \exp(-\eta^2)\mathrm{d}\eta \] 代入\(f(\infty=0)\)，可以得到： \[ A = -2/\sqrt{\pi} \] 于是得到解为： \[ \begin{aligned} f(\eta) &= 1 - \erf(\eta) \\ \erf(\eta) &= \frac{2}{\sqrt{\pi}}\int_0^\eta\exp(-\lambda^2)\mathrm{d}\lambda \end{aligned} \] 形式为\(\theta = \theta_0 f(\eta)\)​​​的解存在，表明了在时间空间的不同点上，只要\(\eta\)​相同，无量纲的\(\theta/\theta_0\)总是相同的，称该解具有自相似性。