半导体中的电子运动及迁移率模拟
半导体中的电子运动及迁移率模拟
电子的运动
在经典的图像里,电子有质量,电子受到电场力产生了加速度,在加速度的作用下,电子速度增加发生了运动,但是这个图像在能带理论里已经摒弃了。实际上,在固体内电场力的作用引起了电子动量的变化,进而引起了电子波矢态\(\mathbf{k}\)的变化, \[ \mathbf{E}q = \frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = \hbar \frac{\mathrm{d}\mathbf{k}}{\mathrm{d}t} \] 波矢态\(\mathbf{k}\)的变化相应地使得电子波包群速度发生变化, \[ \mathbf{v}_g(\mathbf{k}) = \frac{1}{\hbar} \frac{\partial \epsilon}{\partial \mathbf{k}} = \frac{\partial \epsilon}{\partial \mathbf{p}} \] 波包群速度就是能带里能量对动量的偏导,波矢态\(\mathbf{k}\)确定了,电子运动的速度就确定了。
电子可以取到的波矢\(\mathbf{k}\),离散地分布到允许的能带中。所以从净的效果来看,电子之所以能够被电场力加速,就是因为它的波矢态是可以在动量守恒的条件下、在电场力的作用下发生相应变化的。根据泡利不相容原理,不能有两个或两个以上的电子处于完全相同的态,如果所有允许的态都被电子填满了,电子的波矢无法发生相应变化,自然也就无法被电场力加速了,也就没有电流了,所以宏观体现为不导电。当然实际过程可能是说有一个电子被电场力加速,它的态发生了变化,跑到了另一个态上,另一个态的电子无处可去,只能回到这个电子之前的态上,宏观体现为外加了电场,里面电子的状态没有发生任何改变,没有电子被电场力加速,自然也就没有电流了,这里已经完全不再类似于经典的受力加速图像了。电子在半导体中受电场力的驱动在实空间中运动,但是在半导体的某个位置电子所能取到的状态,受到当地的能带结构约束,而并不是像真空的自由电子一样可以随意的被加速和移动,这也是为什么必须借助能带图来理解电子在某个结构中的分布和运动。

迁移率模拟

用蒙特卡洛模拟来计算电子迁移率,可以非常直观地认识迁移率、能带和色散关系的物理意义,以及电子到底是如何在半导体内运动的,郝跃老师的书里对氮化镓中的电子在电场力下运动的过程有一些描述:
GaN电子的漂移速度首先随外电场强度的增大而上升,随后在一个较强的电场强度达到峰值(对于纤锌矿结构,约180kV/cm);电场继续增强,则出现一个速度逐渐下降的广阔负微分电阻区,直到在足够强的电场下速度达到电子饱和速度(约\(1.5\times 10^7\text{cm/s}\))。由于具有较高的击穿电场强度(GaN为\(3\times 10^6\text{V/cm}\)以上,AlN为\(12\times 10^6\text{V/cm}\)以上),GaN材料和AlN材料可以承受很强的电场。低场下电子都位于导带中最低的\(\Gamma\)谷,速度和电场呈近似线性关系,其比例系数即为低场迁移率;当电场增强时,电子能量增加,有机会进入能量较高、有效质量也较大的卫星谷,令迁移率总体呈下降趋势,但GaN中\(\Gamma\)谷中的电子有效质量较大、室温下极性光学声子散射左右很强以及\(\Gamma\)谷和卫星谷之间较大的能量间距,使得电子的谷间转移在较高的电场下才能大规模出现,此时电子的漂移速度达到峰值。当电子进入卫星谷后,其动能和速度减小,有效质量变大,令电子漂移能力变弱,形成负微分电阻特性;电场继续增加时,电子继续向卫星谷转移,电子能量仍上升,但有效质量大且新的谷间形变势散射成为有效的散射机制,是的电子能量随电场增加的速度变慢。两者的综合作用导致形成了广阔的负微分电阻区,最后电子速度达到饱和。
电子在给定半导体的能带中受到电场力作用,动量改变,引起波矢\(\mathbf{k}\)的变化,因为电子能够取到的态分布在导带上,这个过程沿着某一个能带进行,此时这个电子的能量和动量关系(即决定了它在电场力下如何运动的关系,色散关系),由它当前所处的能带位置决定(比如下面图中的不同能带即不同的线上,能量动量关系是不一样的)。在运动的过程中,电子可能会发生散射,跳跃到同一个能带中的其他位置(谷内散射,intravalley scattering)或者跳跃到不同的能带中(谷间散射,intervalley scattering)。注意这种跳跃只是电子的状态发生了跳跃,电子在实空间中的位置是不发生改变的。散射后,电子运动的能量动量关系由跳跃后抵达的能带位置决定,在电场力的作用下沿着新的能带运动,直到发生下一次散射,在这个过程中,一般认为导带是足够空的。所以从这个讨论可以看到,和真空中的自由电子完全不同,并不是电子能量越高则电子的速度越高,因为能带不再是一个简单的抛物线了。什么情况下电子的迁移率会大一些,就是当它运动在一个有效质量低(抛物线比较陡峭)且散射强度也较低的谷中,如果电子的能量很高但运动在一个有效质量大(抛物线比较平缓)的谷中,它的迁移率实际上很低。

用蒙特卡洛方法模拟体材料迁移率的程序,总的来说可以为两个部分,
- 模拟前:准备好半导体的能带信息和各散射机制的散射率,以数组形式存储
- 模拟中:初始化电子们,在每一时间步中对每一个电子处理电场加速和散射过程,同时记录当前步的电子信息
体材料迁移率的模拟只发生在动量空间,不涉及实空间的边界条件,不需要自洽地求解泊松方程,这简化了模拟流程,而且在迁移率模拟中虽然本质上叫作Ensemble模拟,实际上各个电子的运动是彼此独立的。原始的程序来自于https://nanohub.org/wiki/BMC,亚利桑那州立大学的Dragica Vasileska老师在2000年左右开源供大家学习的Fortran程序,这里简单地用Python针对硅重新写了一遍,没有采用像numba或者向量化这些加速操作,大概比原始的Fortran程序慢了300倍左右。
模拟准备
能带
可以参考硅的能带结构 - a Monte Carlo view,这里以硅的非抛物Kane带为例,也可以替换成一些DFT计算的结果,实际上原理都是一样的。硅一共有六个等价的导带,导带底部可以用椭球来描述。

对于第s个导带椭球,它的表达式可以写成 \[ E_k^s\left(1+\alpha E_k^s\right)=\frac{\hbar^2}{2}\left[\frac{\left(k_x-k_{0, x}^s\right)^2}{m_x^*}+\frac{\left(k_y-k_{0, y}^s\right)^2}{m_y^*}+\frac{\left(k_z-k_{0, z}^s\right)^2}{m_z^*}\right] = \gamma \] 其中\(k_{0, x}^s, k_{0, y}^s, k_{0, z}^s\)代表这个椭球的中心坐标,\(\alpha\)称为非抛物因子,这里取为\(0.5 \,\mathrm{eV}^{-1}\),这里在计算的时候要非常小心,因为\(\alpha\)是带能量量纲的,semiconductor people喜欢用电子伏特和厘米作为单位制,如果使用标准单位计算的话,\(\alpha\)的值要除以一个电子伏特。沿椭球方向的等效质量设置为\(0.91m_0\),垂直椭球方向的等效质量设置为\(0.19m_0\)。当然椭球可能不太好处理,我们可以简单地做一下坐标变换,我们定义一个电导有效质量\(m_c\),
\[ m_c = \frac{3}{\frac{1}{m_l} + \frac{2}{m_t}} \] 假设对于长轴位于x轴的椭球,可以定义\(k_x = k_x^\prime \sqrt{m_l / m_c}, k_y = k_x^\prime \sqrt{m_t / m_c}, k_z = k_z^\prime \sqrt{m_t / m_c}\),且由于电子的性质只和偏离导带底部的位置有关,我们可以只考虑偏离导带底的波矢部分,把所有的椭球都平移到布里渊区的零点,同时也不需要真的模拟六个椭球导带,只需要模拟三个互相正交的椭球导带就可以了,因为波矢的绝对值不影响电子性质,只要导带椭球在布里渊区里摆放的方向是一样的,实际上电子在里面运动就是一样的。将上述坐标变换代回能带的表达式中,得到
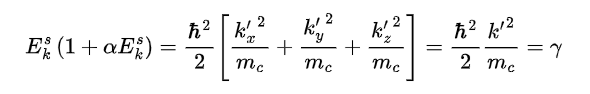
这会给波矢初始化和能量评估带来一些简便性。假设我们已经得到电子的波矢值了,那么可以解出来能量的表达式为 \[ E = \frac{-1 + \sqrt{1 + 4\alpha \gamma} }{2\alpha} = \frac{2\gamma}{\sqrt{1 + 4\alpha \gamma} + 1} \] 因为\(\sqrt{1+4\alpha\gamma}\)和1的差距很小,我们在数值计算里要避免这种两个相差很小的数相减的情况,因此上面的表达式转换成了最右边的式子以保持数值精度。
群速度表达式为 \[ v_x =\frac{1}{\hbar} \frac{E}{\partial k_x} = \frac{\hbar k_x^\prime}{1+2\alpha E} \sqrt{1/(m_l m_c)} \]
此时假如在x方向的电场力作用下运动了\(\tau\)时间,那么x方向的经坐标变换后的波矢变化就是 \[ \mathrm{d}k_x^\prime = - \frac{1}{\hbar}E_x q \tau \sqrt{m_c / m_l} \] #### 散射率
实际模拟过程中为了简化散射率的计算,一般是按照能量分成小段,把散射率储存成查找表,而不是每对应一个状态就重新计算一次散射率。比如我们假设电子在模拟过程中最高可以取到的能量是1eV,把\(0\sim 1\,\mathrm{eV}\)离散成n_lev=1000个小段,把每一段的各个散射机制对应的散射率都储存成一个数组,散射率这个数组中抽样,超出1eV的电子散射率也都按照1eV去处理。可以参考Electron Monte Carlo (1) - 散射,这里只选取了五种散射机制,包括g-intervalley吸收散射,g-intervalley发射散射,f-intervalley吸收散射,f-intervalley发射散射,以及谷内声学声子散射,没有考虑离子库伦散射。这五个散射都可以认为是各向同性散射,这里的各向同性指的是相对椭球来说的各向同性,也就是坐标变换后的\(k_x^\prime, k_y^\prime, k_z^\prime\)是各向同性的,可以按照各向同性抽样去抽取散射后新的波矢大小,这里可以参考蒙特卡洛中的采样。
下面时各种散射率随着电子能量变化的示意图,这里的能量均以导带底作为原点。从各种机制下散射率的大小可以清楚地看到电子的运动在电场力和晶格散射的作用下是如何达到平衡的。起初,电子能量较低,散射率较低,电子自由飞行,从电场中获得能量,能量增加。随着能量的增高,散射率逐渐增加,在各种散射机制中,发射声子的g/f的谷间散射占据了绝对优势,因此每发生一次散射,电子大概率发射一颗光学声子,此时电子的能量降低。当两种机制达到平衡时,即从电场中获得能量收益和发射声子的能量损失平衡时,电子的运动也就达到了平衡,此时就可以统计电子的平均漂移速度来计算迁移率了。

模拟过程
初始化
处于热平衡状态的电子的平均能量是\(\frac{3}{2}k_BT\),假设系统处于300K,那么先按照高斯分布抽样电子的能量,能量确定后,依据能量抽样电子波矢,最后随机抽样电子所处的valley。初始化完所有的电子以后,对每一个电子抽样初次的自由飞行时间。
漂移-散射
整个Ensemble蒙特卡洛模拟的逻辑是这样的,模拟沿着时间推进,每一个时间步的间隔是\(\mathrm{d}t\),在每一个时间步里模拟这个电子的行为。首先,对于每一个电子,我们要抽取它在发生散射前的飞行时间,由下面这个式子确定, \[ \tau = -\ln(r) /\Gamma_m \] 其中\(\Gamma_m\)是一个人为选取的固定值,这个数值大于模拟体系中可能出现的最大散射率,这里引出了电子蒙特卡洛模拟中重要的自散射(self-scattering)的概念,相关的讨论可以参考Electron Monte Carlo (1) - 散射。抽样出了\(\tau\)以后,这时候根据\(\tau\)的数值存在两种可能性,如果\(\tau>\mathrm{d}t\),这说明在当前这个时间步里这颗电子没有被散射,它一直在被电场加速,此时,新的\(\tau = \mathrm{d}t - \tau\)。如果\(\tau < \mathrm{d}t\),这说明这个电子被电场加速了\(\tau\)的时间后,发生了散射,这时在模拟中,我们让这个自由电子自由飞行\(\tau\)的时间,然后根据它飞行后的能量,抽样散射的机制,根据对应的机制,更新散射后这颗电子的波矢、能量、所处的valley信息,之后,再次抽样它的自由飞行时间\(\tau_\text{new}\),如果\(\tau_\text{new} + \tau > \mathrm{d}t\),那么此时的情况就和第一种情况一样了,这颗电子在电场的作用下自由飞行完剩下的\(\mathrm{d}t - \tau\)的时间,在当前时间步结束后距离下一次散射的时间就变成了\(\tau = \tau_\text{new} + \tau - \mathrm{d}t\)。如果还是\(\tau_\text{new}<\mathrm{d}t-\tau\),那么就重复这个抽样-飞行-散射的过程,直到\(\tau_\text{new} > \mathrm{d}t - \tau\)。
Code
MC class
1 | import os |
a single run
1 | mc = MC(simulation_time=5e-12, electric_y=5e6) |
begin simulation... (∪.∪ )...zzz
100%|██████████| 501/501 [00:16<00:00, 30.79it/s]
simulation ends... (^∀^●)ノシ
1 | # scattering calculation |
能量随时间的演化:
1 | plt.plot(mc.hists[:, 0]/1e-12, mc.hists[:, 1]/c.e) |

漂移速度随时间的演化:
1 | plt.plot(mc.hists[:, 0]/1e-12, mc.hists[:, 2]/1e5, label=r'$v_x$') |

迁移率模拟
1 | fys = [2e4, 5e4, 1e5, 5e5, 1e6, 5e6, 7e6] |
