科勒尼希-彭尼模型
Kronig-Penny Model
Thank you Anish for the introduction about electron-phonon Monte Carlo methods.
克勒尼希-彭尼模型描述了势能周期性对电子能级的影响,实际上就是求解了单一电子、一维矩形周期势的能量本征方程。
二阶常系数齐次线性微分方程的通解
对于二阶常系数线性方程, \[ y^{\prime\prime} + py^{\prime} + qy = 0 \] 特征根为 \[ r_{1,2} = \frac{-p \pm \sqrt{p^2 - 4q}}{2} \] 若有两个不相等的实根,则齐次方程的通解为, \[ y = C_1e^{r_1x} + C_2 e^{r_2x} \] 若有两个相等的实根,则齐次方程的通解为, \[ y = C_1e^{r_1x} + C_2xe^{r_1x} \] 若有一对共轭复根,\(r_1 = \alpha + i \beta, r_2 = \alpha - i\beta\),则齐次方程的通解为, \[ y = C_1e^{r_1x} + C_2 e^{r_2x} \] 或者可以写成, \[ y = e^{\alpha x}\left(C_1\cos\beta x + C_2 \sin\beta x\right) \]
一维周期势能模型
一维定态薛定谔方程(能量本征方程)具有如下形式, \[ \begin{aligned} \left(-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2} + U\right)\psi &= E\psi\\ \frac{\mathrm{d}^2 \psi}{\mathrm{d}x^2} + \frac{2m}{\hbar^2}(E-U)\psi &= 0\\ \end{aligned} \] 左边是哈密顿算符,右边是哈密顿算符的本征值-能量,无论是一维无限深方阱、有限势垒导致的量子隧穿还是周期性势场,方程及通解的形式都是一样的,只是边界条件对解的具体表达式有些影响。
在Kronig-Penny模型中,势能具有如下形式:
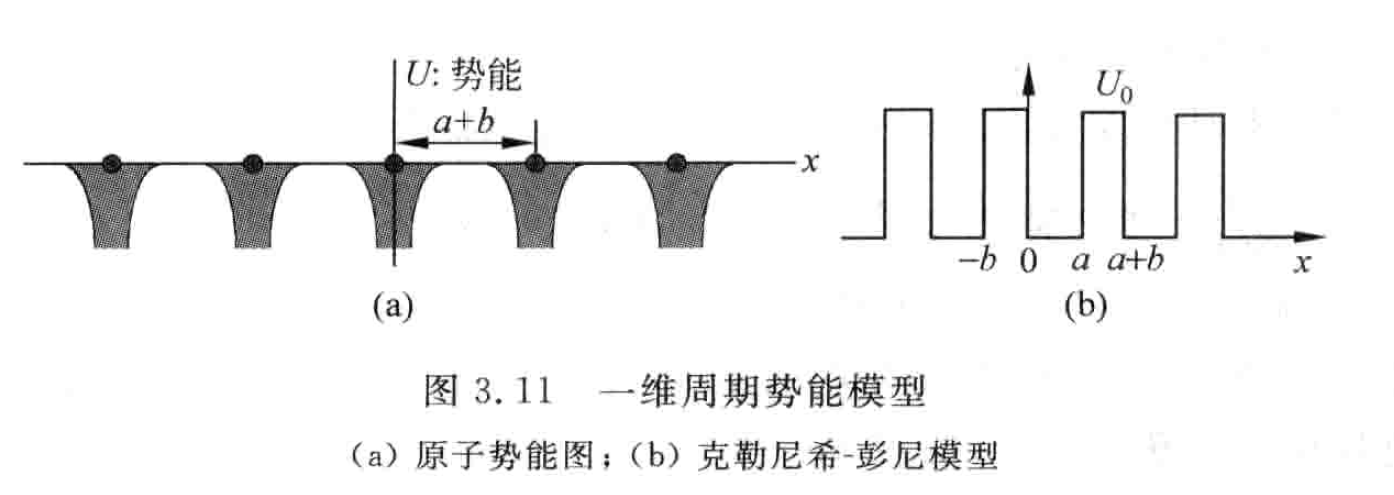
势能函数\(U(x)\)为, \[ U(x)=\left\{\begin{array}{cc} 0, & 0<x \leqslant a \\ U_{0}, & -b<x \leqslant 0 \end{array}\right. \] 同时服从周期性要求, \[ U(x + a + b) = U(x) \] 在势垒外部,\(U = 0\),此时解的形式是向左及向右传播的自由行波解, \[ \psi = A\mathrm{e}^{iKx} + B\mathrm{e}^{-iKx}, K = \frac{\sqrt{2mE}}{\hbar} \] 在势垒内部, \[ \psi = C\mathrm{e}^{Qx} + D\mathrm{e}^{-Qx}, Q = \frac{\sqrt{2m(E - U_0)}}{\hbar} \] 需要四个边界条件来确定\(A,B,C,D\)
根据波函数及其导数在\(x = 0\)处的连续性,可以得到两个边界条件, \[ \begin{aligned} A+B &= C+D \\ iK(A-B) &= Q(C-D) \end{aligned} \]
Block Theorem
布洛赫定理,对于含有周期势的薛定谔方程,其解必然具有如下形式, \[ \psi(\mathbf{r} + \mathbf{R}) = \psi(\mathbf{r}) \exp(i\mathbf{k}\cdot \mathbf{R}) \] 其中\(\mathbf{R}\)是原胞点阵的格矢,原胞中可能包含多个离子,比如纤锌矿GaN一个晶胞中包含两对离子。不管原胞里面的东西,把原胞抽象成质点,可以研究晶格的周期性排列情况。 \(\mathbf{R}\)就代表从一个原胞格点指向另一个原胞格点的矢量,通过对\(\mathbf{R}\)的定义,我们可以从一个格点出发,确定任何其他原胞格点的位置,\(\mathbf{r}\)和 \(\mathbf{r} + \mathbf{R}\)代表晶体内部的两个等价格点。其中\(\mathbf{k}\)代表晶格的波矢,它与晶格振动和声子能量有关,电子薛定谔方程中的传播矢量\(\mathbf{K}\)与电子能量有关,这两个是不同的概念。
布洛赫定理指出,在晶体内部两个等价点\(\left( \mathbf{r}\text{和}\mathbf{r} + \mathbf{R} \right)\)的波函数值只差一个相位因子\(\exp(i\mathbf{k}\cdot\mathbf{R})\),于是我们只要知道了一个单胞内的波函数,就可以得到整个晶体的波函数了。这实际上意味着晶体中的原胞排列是周期性的,其波函数也具有同样的周期性。
对于一维线性晶格,存在 \[
\psi\left( x + a + b \right) = \psi(x)\exp\left(ik (a + b) \right)
\] 由布洛赫定理可知,如果波函数在区间\(-b < x < 0\),可由上面推导的方程的形式给出;如果波函数在区间\(a < x < a+b\),可由\(-b < x < 0\)区间的波函数乘以相位因子给出。利用波函数及其导数在\(x=a\)处的连续性,可以得到另外两个边界条件, \[
\begin{aligned}
A \mathrm{e}^{\mathrm{i} K a}+B \mathrm{e}^{-i K a}&=\left(\mathrm{Ce}^{-Q b}+D \mathrm{e}^{Q b}\right) \exp [\mathrm{i} k(a+b)] \\
\mathrm{i} K\left(A \mathrm{e}^{i K a}-B \mathrm{e}^{-\mathrm{iKa}}\right)&=Q\left(C \mathrm{e}^{-Q b}-D \mathrm{e}^{Q b}\right) \exp [\mathrm{i} k(a+b)]
\end{aligned}
\] 于是现在共得到了四个边界条件, \[
\begin{aligned}
A+B &= C+D \\
iK(A-B) &= Q(C-D)\\
A \mathrm{e}^{\mathrm{i} K a}+B \mathrm{e}^{-i K a}&=\left(\mathrm{Ce}^{-Q b}+D \mathrm{e}^{Q b}\right) \exp [\mathrm{i} k(a+b)] \\
\mathrm{i} K\left(A \mathrm{e}^{i K a}-B \mathrm{e}^{-\mathrm{iKa}}\right)&=Q\left(C \mathrm{e}^{-Q b}-D \mathrm{e}^{Q b}\right) \exp [\mathrm{i} k(a+b)]
\end{aligned}
\] 根据Cramer法则,系数行列式为0时方程有非平凡解, \[
\left | \begin{matrix}
1 & 1 & -1 & -1 \\
iK & -iK & -Q & Q \\
e^{iKa} & e^{-iKa} & -e^{-Qb}\exp [\mathrm{i} k(a+b)] & -e^{Qb}\exp [\mathrm{i} k(a+b)] \\
iKe^{iKa} & iKe^{-iKa} & -Qe^{-Qb}\exp [\mathrm{i} k(a+b)] & Qe^{Qb}\exp [\mathrm{i} k(a+b)] \\
\end{matrix} \right | = 0
\] 得到, \[
\frac{Q^{2}-K^{2}}{2 K Q} \sinh (Q b) \sin (K a)+\cosh (Q b) \cos (K a)=\cos \left[k(a+b)\right]
\] 对于给定的波矢\(k\),上式只有电子能量\(E\)未知,其隐含在\(K\)和\(Q\)中,上式可以用来确定\(E\)和\(k\)之间的关系。这个方程的形式是比较复杂的,为了简化这个结果,取极限\(b\rightarrow 0, U_0\rightarrow 0\),即势垒无限窄、无限高,保持\(Q^2ba/2=P\)为常数。在这种近似下,\(Q \gg K, Qb \ll 1\),于是\(\sinh(Qb)\approx 0, \cosh(Qb)\approx1\),上式简化为, \[
\frac{P}{K a} \sin K a+\cos K a=\cos k a
\] 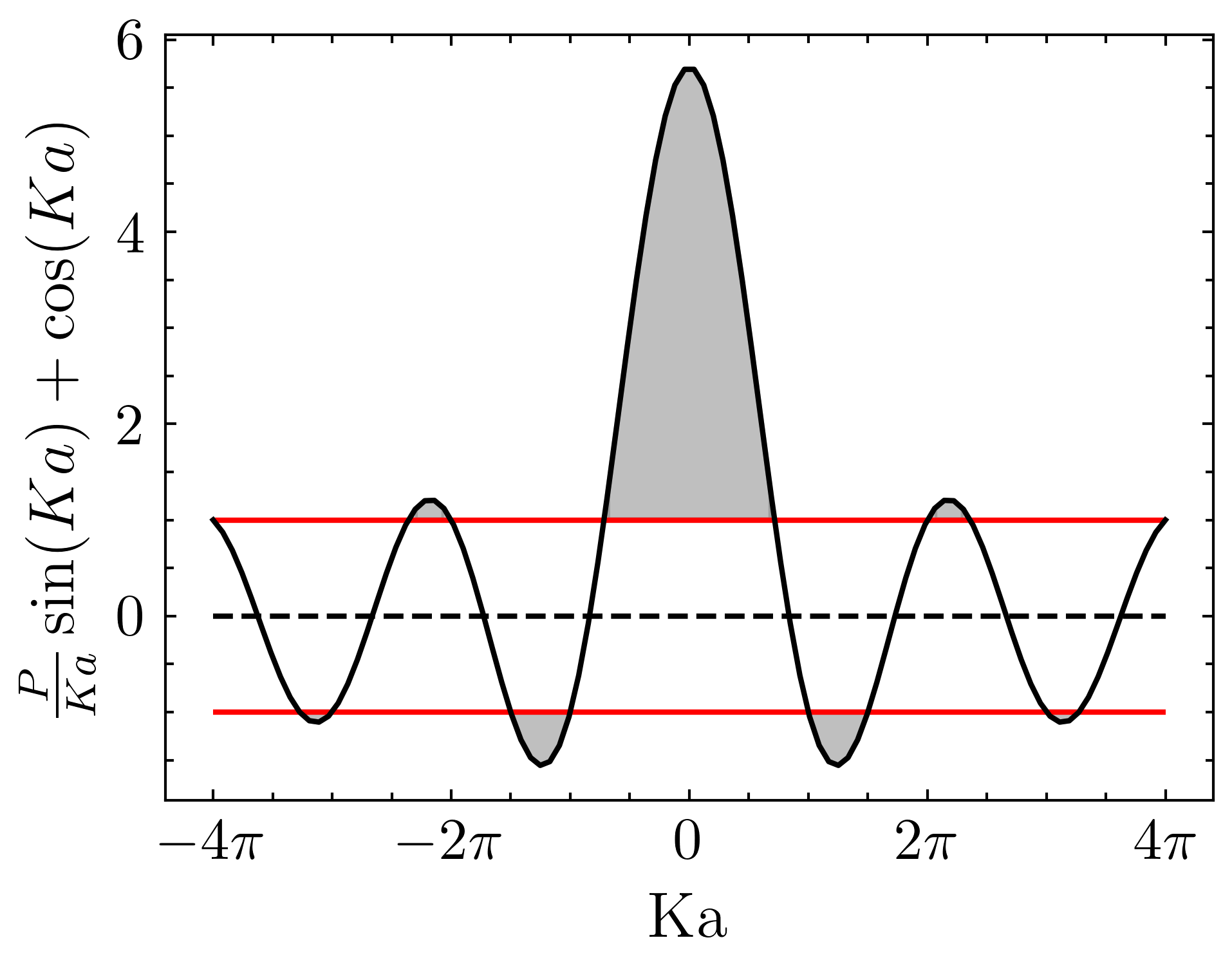
\(\cos(ka)\)永远小于1,所以只有上式左侧小于1的时候,这个方程才可能有解,上图是方程在\(P = 3\pi/2\)时方程左侧随\(Ka\)变化的情况,在阴影区域,\(K\)没有解,因而没有能量与该\(K\)值对应的电子存在。
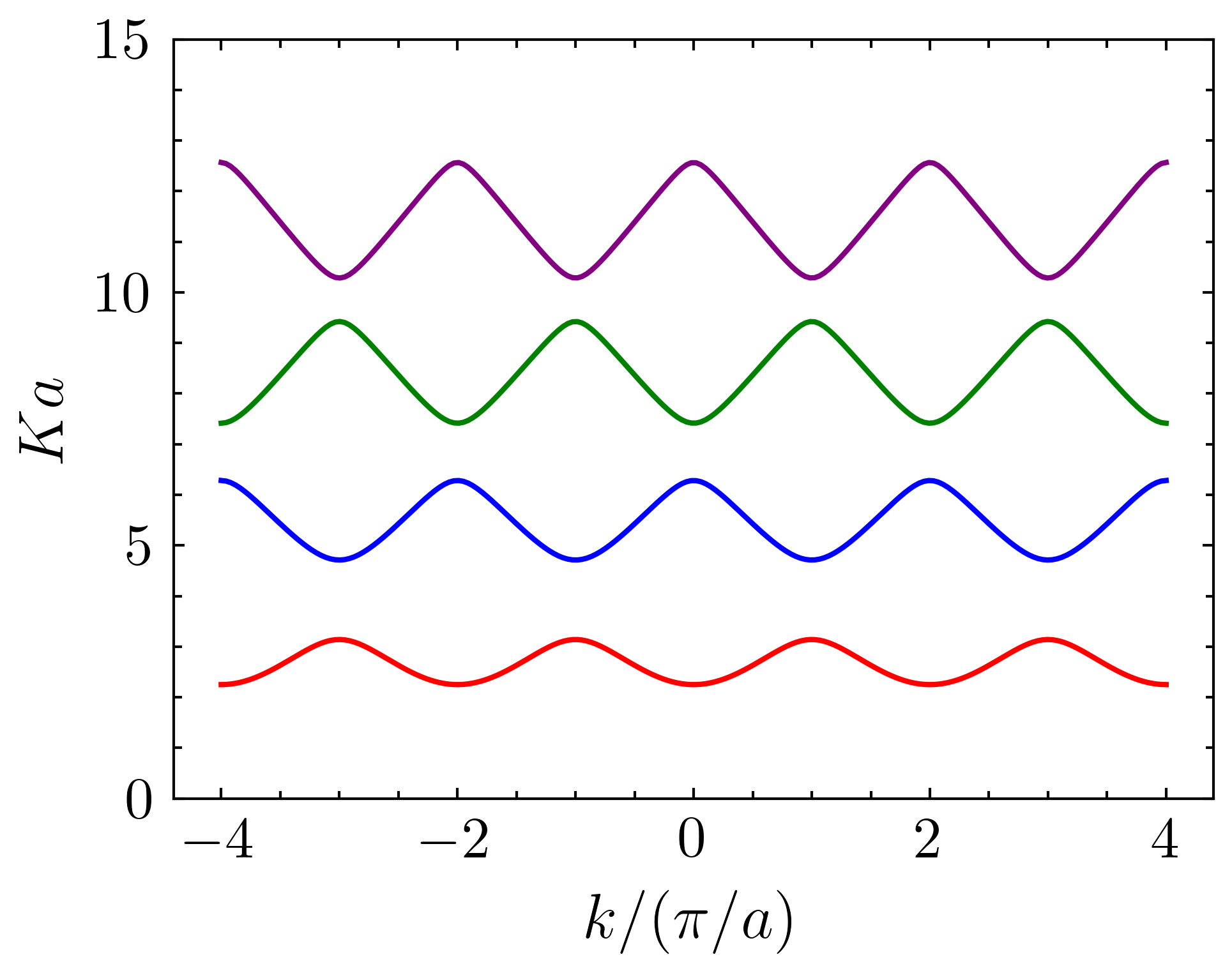
电子能带的简单计算
从图中可以看到,对于同一个晶格常数和波矢\(k\),\(\cos ka\)和方程左侧存在多个交点,即一个\(ka\)对应着多个电子\(Ka\),而\(Ka\)就对应着电子能量: \[ \frac{\hbar^2 K^2}{2m} = E \] 通过选取不同的初值,可以计算出电子能带,
1 | import numpy as np |