薄膜声子导热解析解

好喜欢weihan公主👸!

Problem Statement

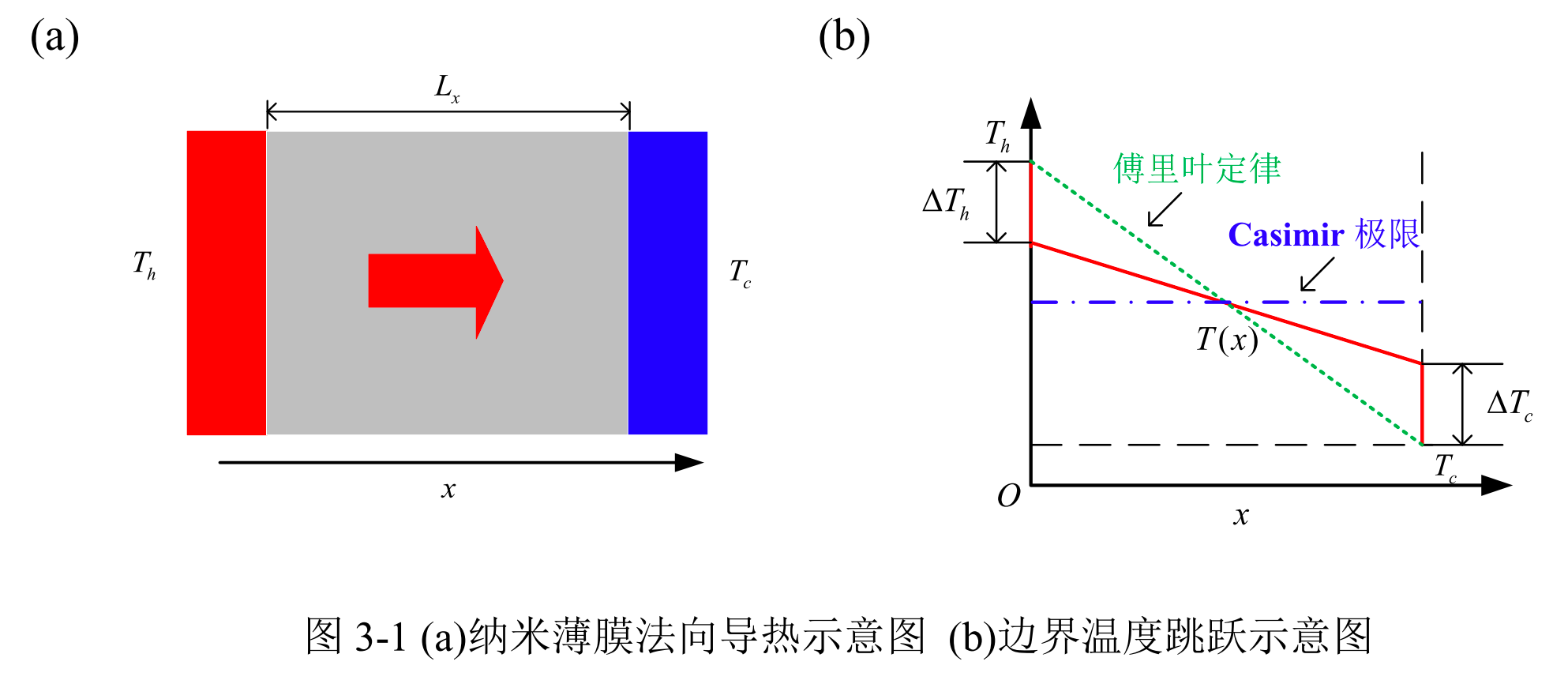
一边高温热沉，一边低温热沉。虽然这个问题是一维的，我们还是要建立球坐标系，因为它涉及对立体角的积分，为了方便对问题的处理，把\(x\)方向当作一般球坐标系的\(z\)轴。求解问题的一些基础知识可以参考以前的推送。

求解过程

内部某点热流表达式（这里为了简便都没写声子支）： \[ q_x = \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}f_\omega v_g\mathrm{d}\omega \] 根据线性化的玻尔兹曼方程，有： $$

\[\begin{aligned} f &= f^0 - \tau \boldsymbol{v_g}\cdot \nabla f^0 \\ &= f^0 - \tau v_g\cos\theta \frac{\mathrm{d}f^0}{\mathrm{d}x} \\ &= f^0 - \tau v_g\cos\theta \frac{\mathrm{d}f^0}{\mathrm{d}T} \frac{\mathrm{d}T}{\mathrm{d}x} \end{aligned}\] \[ 代入到热流表达式中，有： \] \[\begin{aligned} q_x &= \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}f_\omega v_g\mathrm{d}\omega\\ &= - \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi}\cos^2\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}\frac{\mathrm{d}f^0}{\mathrm{d}T} \tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}\\ &= - \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi}\cos^2\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\frac{C(\omega)}{4\pi} \tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}\\ &= - \frac{1}{3} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}\\ &= -k \frac{\mathrm{d}T}{\mathrm{d}x},\quad k = \frac{1}{3} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \end{aligned}\]

$$ 高温边界处的净热流为高温热沉发射的热流减去返回边界的负向热流：

\[ q_b = q_x^+ - q_x^{-} \]

其中 \[ \begin{aligned} q_x^+ &= \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi/2}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}f_\omega^0 (T_h) v_g\mathrm{d}\omega\\ \end{aligned} \] 在小温差近似下，有： \[ \hbar\omega D(\omega)(f^0(T) - f^{0}(T_{ref})) \approx C(\omega)(T - T_{ref}) \] 于是 \[ \begin{aligned} q_x^+ - q_{ref} &= \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi/2}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}\left(f_\omega^0 (T_h) - f_\omega^0 (T_{ref}) \right) v_g\mathrm{d}\omega\\ & \approx \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi/2}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\frac{C(\omega)(T_h - T_{ref})}{4\pi}v_g\mathrm{d}\omega\\ &= \frac{1}{4}\int_0^{\omega_m}C(\omega)(T_h - T_{ref})v_g \mathrm{d}\omega \end{aligned} \] \(q_x^-\)为 \[ \begin{aligned} q_x^{-} &= \int_0^{2\pi}\mathrm{d}\phi \int_{\pi/2}^{\pi}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}f_\omega v_g\mathrm{d}\omega\\ &= - \int_0^{2\pi}\mathrm{d}\phi \int_{0}^{\pi}\cos\theta\sin\theta \mathrm{d}\theta\int_0^{\omega_m}\hbar\omega \frac{D(\omega)}{4\pi}\left(f^0(T|_{x=0}) - \tau v_g\cos\theta \frac{\mathrm{d}f^0(T|_{x=0})}{\mathrm{d}T} \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0}\right)v_g\mathrm{d}\omega\\ \end{aligned} \]

把这个表达式分成两部分，\(f^0(T)\)按照对热沉求解时一样操作，梯度部分按照内部处理，于是可以得到： \[ q_x^- - q_{ref} = \frac{1}{4}\int_0^{\omega_m}C(\omega)(T|_{x=0} - T_{ref})v_g \mathrm{d}\omega + \frac{1}{6} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} \] 于是净热流为： \[ \begin{aligned} q_b &= \left(q_x^+ - q_{ref}\right) - \left( q_x^- - q_{ref} \right) \\ &= \frac{1}{4}\int_0^{\omega_m}C(\omega)(T_h - T|_{x=0})v_g \mathrm{d}\omega - \frac{1}{6} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} \end{aligned} \]

根据热流连续性条件： \[ q_b = q|_{x=0} \] 于是

\[\begin{aligned} \frac{1}{3} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0}&=\frac{1}{4}\int_0^{\omega_m}C(\omega)(T_h - T|_{x=0})v_g \mathrm{d}\omega - \frac{1}{6} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} \end{aligned}\]

即 \[ \begin{aligned} - \frac{2}{3} \frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega&= (T_h - T|_{x=0}) \int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega \end{aligned} \] 得到边界温度跳跃为： \[ T_h - T|_{x=0} = - \frac{2}{3} \frac{ \int_0^{\omega}C(\omega)\tau v_g^2\mathrm{d}\omega}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega}\frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} = - \frac{ 2k}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega}\frac{\mathrm{d}T}{\mathrm{d}x}|_{x=0} = \frac{2k(T|_{x=0} - T|_{x=L})/L}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega} \] 同理可以得到低温边界处的温度跳跃： \[ T|_{x=L} - T_c = - \frac{ 2k }{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega}\frac{\mathrm{d}T}{\mathrm{d}x}|_{x=L} = \frac{2k(T|_{x=0} - T|_{x=L})/L}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega} \] 其实两个边界温度跳跃的值都是一样的，把上面两个加起来，可以建立\((T|_{x=0} - T|_{x=L})\)和\((T_h - T_c)\)之间的关系： \[ (T_h - T_c) = \left(\frac{4k/L}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega} + 1\right)(T|_{x=0} - T|_{x=L}) = (4A+1)(T|_{x=0} - T|_{x=L}) \]

\[ A = \frac{k/L}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega} \]

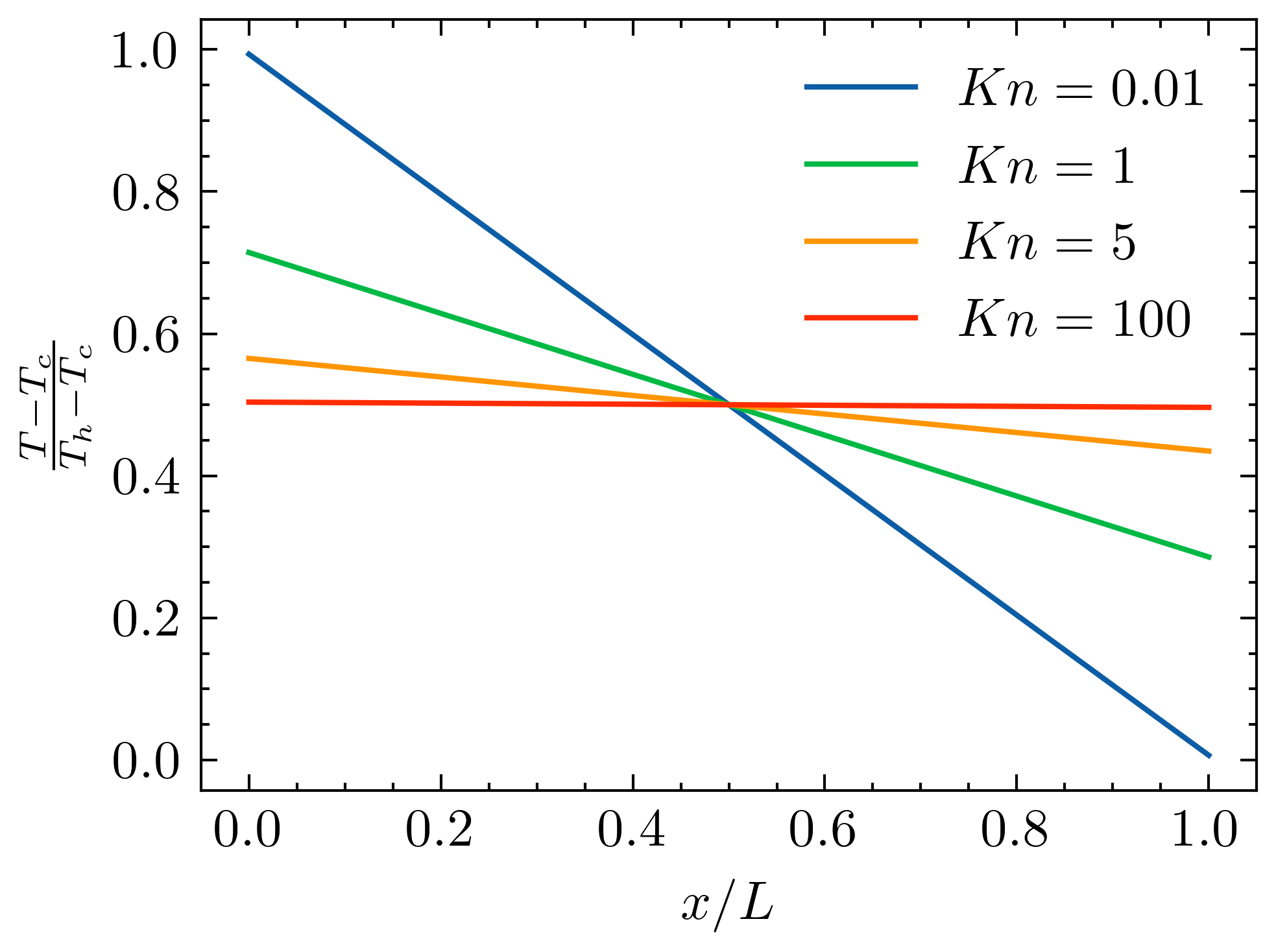
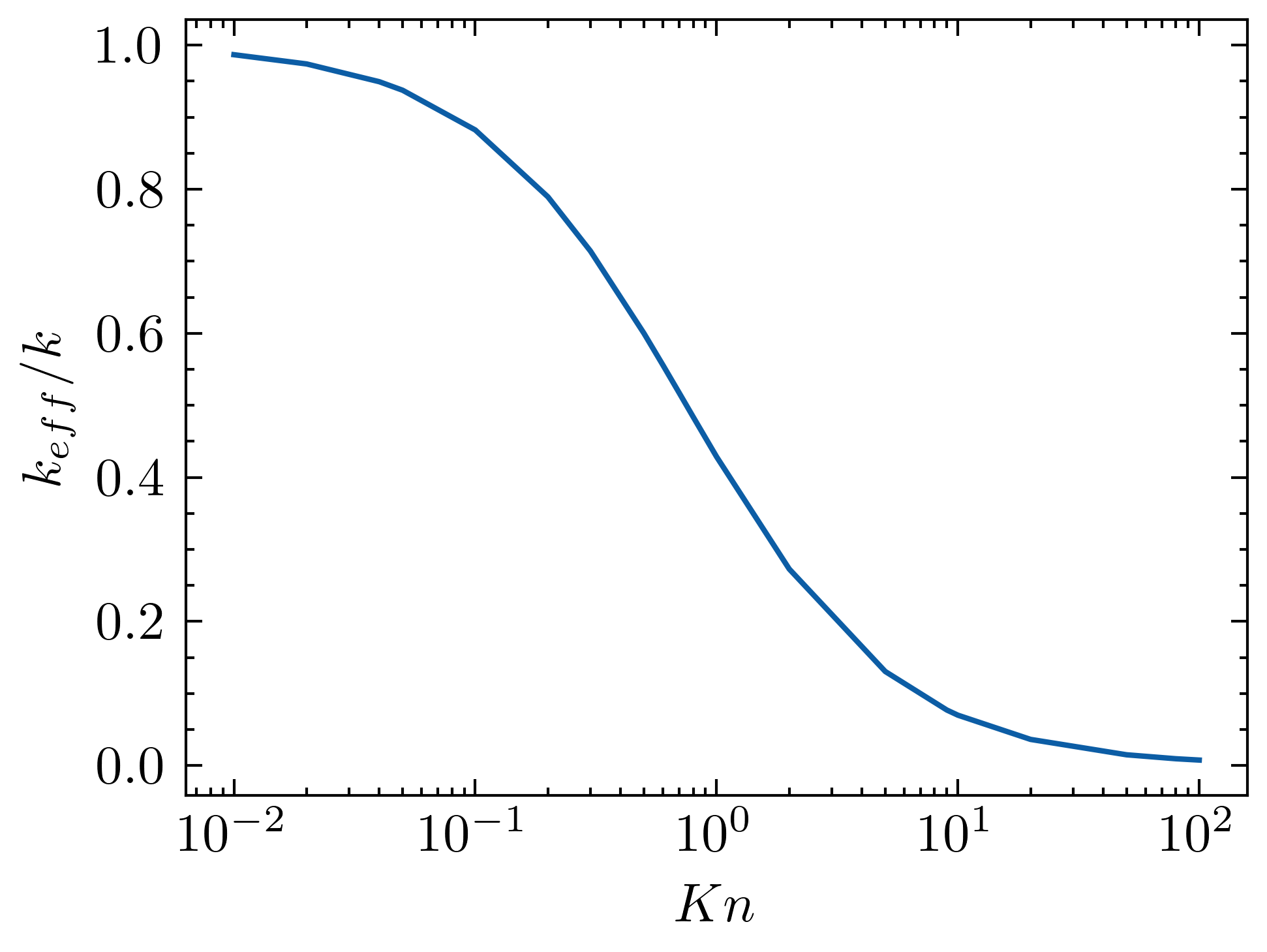
温度跳跃的值为： \[ \Delta T_{jump} = 2A(T|_{x=0} - T|_{x=L}) = \frac{2A}{4A+1}(T_h - T_c) \] 在灰体近似下，有： \[ A = \frac{k/L}{\int_0^{\omega_m}C(\omega)v_g \mathrm{d}\omega} = \frac{1}{3}\frac{ Cv_gl_{ave}}{Cv_gL} = \frac{1}{3}\frac{l_{ave}}{L} = \frac{1}{3}Kn \] 根据内部热流关系式，可以发现内部还是满足傅立叶定律，温度还是呈线性分布的，根据温度跳跃，可以得到薄膜内部的温度分布： \[ \begin{aligned} T &= - \frac{T|_{x=0} - T|_{x=L}}{L}x + T|_{x=0} \\ &= - \frac{T_h - T_c}{4A+1}\frac{x}{L} + T_h - \frac{2A}{4A+1}(T_h - T_c) \\ &= \frac{1}{4A +1}\left[ -(2A + \frac{x}{L})(T_h-T_c) + T_h \right] \end{aligned} \] 薄膜的法向等效热导率定义为： \[ q = k_{eff} \frac{T_h - T_c}{L} = -k\frac{\mathrm{d}T}{\mathrm{d}x} \] 于是 \[ k_{eff}/k = \frac{-\dfrac{\mathrm{d}T}{\mathrm{d}x}}{(T_h - T_c)/L} = \frac{1}{4A + 1} \] 等效热导率和体材料热导率的比，实际上就是建立起来的温度梯度之比。为什么弹道极限下等效热导率为0..倒不是没有热流了，只是温度定义不出来了..

在灰体近似下，有： \[ T = \frac{1}{\frac{4}{3}Kn +1}\left[ - (\frac{x}{L} + \frac{2}{3}Kn)(T_h-T_c) + T_h \right] \]

\[ k_{eff}/k = \frac{1}{\frac{4}{3}Kn + 1} \]