AMM模型和DMM模型

Thermal Boundary Resistance

......人们要想得到工作的胜利即得到预想的结果，一定要使自己的思想合于客观外界的规律性，如果不合，就会在实践中失败。人们经过失败之后，也就从失败取得教训，改正自己的思想使之适合于外界的规律性，人们就能变失败为胜利，所谓“失败者成功之母”，“吃一堑长一智”，就是这个道理。

......然而人的认识究竟怎样从实践发生，而又服务于实践呢？这只要看一看认识的发展过程就会明了的。 　　原来人在实践过程中，开始只是看到过程中各个事物的现象方面，看到各个事物的片面，看到各个事物之间的外部联系。例如有些外面的人们到延安来考察，头一二天，他们看到了延安的地形、街道、屋宇，接触了许多的人，参加了宴会、晚会和群众大会，听到了各种说话，看到了各种文件，这些就是事物的现象，事物的各个片面以及这些事物的外部联系。这叫做认识的感性阶段，就是感觉和印象的阶段。也就是延安这些各别的事物作用于考察团先生们的感官，引起了他们的感觉，在他们的脑子中生起了许多的印象，以及这些印象间的大概的外部的联系，这是认识的第一个阶段。在这个阶段中，人们还不能造成深刻的概念，作出合乎论理（即合乎逻辑）的结论。

......社会实践的继续，使人们在实践中引起感觉和印象的东西反复了多次，于是在人们的脑子里生起了一个认识过程中的突变（即飞跃），产生了概念。概念这种东西已经不是事物的现象，不是事物的各个片面，不是它们的外部联系，而是抓着了事物的本质，事物的全体，事物的内部联系了。概念同感觉，不但是数量上的差别，而且有了性质上的差别。循此继进，使用判断和推理的方法，就可产生出合乎论理的结论来。《三国演义》上所谓“眉头一皱计上心来”，我们普通说话所谓“让我想一想”，就是人在脑子中运用概念以作判断和推理的工夫。这是认识的第二个阶段。外来的考察团先生们在他们集合了各种材料，加上他们“想了一想”之后，他们就能够作出“共产党的抗日民族统一战线的政策是彻底的、诚恳的和真实的”这样一个判断了。在他们作出这个判断之后，如果他们对于团结救国也是真实的的话，那末他们就能够进一步作出这样的结论：“抗日民族统一战线是能够成功的。”这个概念、判断和推理的阶段，在人们对于一个事物的整个认识过程中是更重要的阶段，也就是理性认识的阶段。认识的真正任务在于经过感觉而到达于思维，到达于逐步了解客观事物的内部矛盾，了解它的规律性，了解这一过程和那一过程间的内部联系，即到达于论理的认识。重复地说，论理的认识所以和感性的认识不同，是因为感性的认识是属于事物之片面的、现象的、外部联系的东西，论理的认识则推进了一大步，到达了事物的全体的、本质的、内部联系的东西，到达了暴露周围世界的内在的矛盾，因而能在周围世界的总体上，在周围世界一切方面的内部联系上去把握周围世界的发展。

......我们的实践证明：感觉到了的东西，我们不能立刻理解它，只有理解了的东西才更深刻地感觉它。感觉只解决现象问题，理论才解决本质问题。这些问题的解决，一点也不能离开实践。

......常常听到一些同志在不能勇敢接受工作任务时说出来的一句话：没有把握。为什么没有把握呢？因为他对于这项工作的内容和环境没有规律性的了解，或者他从来就没有接触过这类工作，或者接触得不多，因而无从谈到这类工作的规律性。及至把工作的情况和环境给以详细分析之后，他就觉得比较地有了把握，愿意去做这项工作。如果这个人在这项工作中经过了一个时期，他有了这项工作的经验了，而他又是一个肯虚心体察情况的人，不是一个主观地、片面地、表面地看问题的人，他就能够自己做出应该怎样进行工作的结论，他的工作勇气也就可以大大地提高了。只有那些主观地、片面地和表面地看问题的人，跑到一个地方，不问环境的情况，不看事情的全体（事情的历史和全部现状），也不触到事情的本质（事情的性质及此一事情和其它事情的内部联系），就自以为是地发号施令起来，这样的人是没有不跌交子的。

......要完全地反映整个的事物，反映事物的本质，反映事物的内部规律性，就必须经过思考作用，将丰富的感觉材料加以去粗取精、去伪存真、由此及彼、由表及里的改造制作工夫，造成概念和理论的系统，就必须从感性认识跃进到理性认识。这种改造过的认识，不是更空虚了更不可靠了的认识，相反，只要是在认识过程中根据于实践基础而科学地改造过的东西，正如列宁所说乃是更深刻、更正确、更完全地反映客观事物的东西。庸俗的事务主义家不是这样，他们尊重经验而看轻理论，因而不能通观客观过程的全体，缺乏明确的方针，没有远大的前途，沾沾自喜于一得之功和一孔之见。这种人如果指导革命，就会引导革命走上碰壁的地步。

......这是因为从事变革现实的人们，常常受着许多的限制，不但常常受着科学条件和技术条件的限制，而且也受着客观过程的发展及其表现程度的限制（客观过程的方面及本质尚未充分暴露）。在这种情形之下，由于实践中发现前所未料的情况，因而部分地改变思想、理论、计划、方案的事是常有的，全部地改变的事也是有的。即是说，原定的思想、理论、计划、方案，部分地或全部地不合于实际，部分错了或全部错了的事，都是有的。许多时候须反复失败过多次，才能纠正错误的认识，才能到达于和客观过程的规律性相符合，因而才能够变主观的东西为客观的东西，即在实践中得到预想的结果。但是不管怎样，到了这种时候，人们对于在某一发展阶段内的某一客观过程的认识运动，算是完成了。

论认识和实践的关系——知和行的关系

（一九三七年七月）

毛泽东

子贡问于孔子曰：“赐倦于学，困于道矣，愿息而事君，可乎？”孔子曰：“《诗》云：‘温恭朝夕，执事有恪。’事君之难也，焉可息哉！” 曰：“然则赐愿息而事亲。”孔子曰：“《诗》云：‘孝子不匮，永锡尔类。’事亲之难也，焉可以息哉！” 曰：“然则赐请息于妻子。”孔子曰：“《诗》云：‘刑于寡妻，至于兄弟，以御于家邦。’妻子之难也，焉可以息哉！” 曰：“然则赐愿息于朋友。”孔子曰：“《诗》云：‘朋友攸摄，摄以威仪。’朋友之难也，焉可以息哉！” 曰：“然则赐愿息于耕矣。”孔子曰：“《诗》云：‘昼尔于茅，宵尔索绚，亟其乘屋，其始播百谷。’耕之难也，焉可以息哉！” 曰：“然则赐将无所息者也？”孔子曰：“有焉。自望其广，则睪如也；视其高，则填如也；察其从，则隔如也。此其所以息也矣。” 子贡曰：“大哉乎死也！君子息焉，小人休焉。大哉乎死也！”

孔子家语 卷五 困誓第二十二

接触热阻和边界热阻

接触热阻和边界热阻（TBR）指的是两个概念。接触热阻指的是两个表面通常都非常粗糙的物体之间热阻，两个物体被连接或者机械接合在一起。而TBR指的是即使在两材料理想接触时，由于相邻材料声学特性的存在，声子在向边界传递时还是会发生反射。现实中的分界面可以做到原子量级上的光滑，粗糙度可以达到零点几个纳米。

所以对TBR的建模，很大程度上就是确定射向界面的声子有多少会被反射回来，反射回来得越多，TBR就越大。如果反射率为0，那么TBR就不存在了。对TBR声子散射率的建模，有两个经典的模型，声学失配模型 Acoustic mismatch model（AMM）和扩散失配模型 Diffuse mismatch model （DMM）。

AMM和DMM

在任意给定频率下，声子透射系数可以表述为， \[ \tau_{12}=\tau_{21}=\frac{4 \rho_{1} \rho_{2} v_{l 1} v_{l 2} \cos \theta_{1} \cos \theta_{2}}{\left(\rho_{1} v_{l 1} \cos \theta_{2}+\rho_{2} v_{l 2} \cos \theta_{1}\right)^{2}} \] 透射系数的推导是封装好的另一个level的东西了，可以先放在这里，不影响对AMM方法本身的理解。

公式中下标\(1\)和\(2\)分别代表不同的介质，\(\rho\)是密度，\(v_l\)是纵声学支的声速，\(\theta\)是极角。

入射角和折射角\(\theta_1, \theta_2\)之间的关系可以类比于光学中的斯涅尔定律去近似， \[ \frac{1}{v_{l1}}\sin\theta_1 = \frac{1}{v_{l2}}\sin\theta_2 \] 考虑\(v_{l1} > v_{l2}\)的情况，即声子在介质1中的声速大于在介质2中的声速，当从介质2入射到介质1中时，此时存在一个临界角度\(\theta_c\)， \[ \theta_c = \sin^{-1}(v_{l2} / v_{l1}) \] 此时\(\sin(\theta_1)=1\)，已经无法再增大了，入射角超过\(\theta_c\)部分的声子全部都会被反射过来。

由于边界热阻，在界面处会存在温度跳跃（可以参考多层器件的热阻分析）。假设界面两侧的声子仍然在相应温度保持平衡，可以用Bose-Einstein分布去计算声子的分布函数. 因此，从介质1到介质2的声子热流可以表述为， \[ \begin{aligned} q^{\prime \prime}_{1\rightarrow 2} &= \int_0^{\omega_m}\int_0^{2\pi}\int_0^{\pi/2}\hbar\omega v_{l1}f_1(\omega,T_1)\tau_{12}\frac{D(\omega)}{4\pi}\cos(\theta_1)\sin(\theta_1)\mathrm{d}\theta_1\mathrm{d}\phi\mathrm{d}\omega \\ &= 2\int_0^{\omega_m}\int_0^{2\pi}\hbar\omega v_{l1}f_1(\omega,T_1)\tau_{12}\frac{D(\omega)}{4}\cos(\theta_1)\sin(\theta_1)\mathrm{d}\theta_1\mathrm{d}\omega \\ \end{aligned} \] 定义半球透射率\(\Gamma_{12}\),

\[ \Gamma_{12} = 2\int_{0}^{\pi/2}\tau_{12}\cos(\theta_1)\sin(\theta_1)\mathrm{d}\theta_1 \] 于是介质1到介质2的热流可写为， \[ \begin{aligned} q^{\prime \prime}_{1\rightarrow 2} &= \frac{1}{4}\Gamma_{12}\int_0^{\omega_m}\hbar\omega v_{l1}f_1(\omega,T_1)D(\omega)\mathrm{d}\omega \\ \end{aligned} \] 半球透射率的定义剥离出来了界面两处不同的部分，介质2到介质1的半球透射率可以定义为， \[ \begin{aligned} \Gamma_{21} &= 2\int_{0}^{\pi/2}\tau_{21}\cos(\theta_2)\sin(\theta_2)\mathrm{d}\theta_2 \\ \end{aligned} \]

\(\theta_1\)和\(\theta_2\)满足，

$$ \[\begin{aligned} \frac{1}{v_{l1}}\sin\theta_1 &= \frac{1}{v_{l2}}\sin\theta_2 \\ \frac{1}{v_{l1}}\cos\theta_1 \mathrm{d}\theta_1&= \frac{1}{v_{l2}}\cos\theta_2 \mathrm{d}\theta_2 \end{aligned}\]

$$

于是可以建立\(\Gamma_{12}\)和\(\Gamma_{21}\)的关系，

\[ \Gamma_{21} = \frac{v_{l2}^2}{v_{l1}^2}\Gamma_{12} \]

净热流为，

\[ \begin{aligned} q^{\prime \prime} &= q^{\prime \prime}_{1\rightarrow 2} - q^{\prime \prime}_{2\rightarrow 1} \\ &= \frac{1}{4}\Gamma_{12}\int_0^{\omega_m}\hbar\omega v_{l1}f_1(\omega,T_1)D(\omega)\mathrm{d}\omega - \frac{1}{4}\Gamma_{21}\int_0^{\omega_m}\hbar\omega v_{l2}f_2(\omega,T_2)D(\omega)\mathrm{d}\omega \\ &= \frac{1}{4}\frac{\Gamma_{12}}{v_{l1}^2}\int_0^{\omega_m}\hbar\omega\left[v_{l1}^3 f_1(\omega, T_1) - v_{l2}^3f_2(\omega,T_2)\right]D(\omega)\mathrm{d}\omega \\ \end{aligned} \]

Debye模型假设声子的群速度不随频率发生变化，于是可以计算Debye态密度，

\[ D(\omega) = \frac{k^2}{2\pi^2 v_g} = \frac{\omega^2}{2\pi^2v_g^3} \]

代回净热流公式，同时用\(k_BT\)和\(\hbar\omega_m\)把频率的积分无量纲化，展开玻色-爱因斯坦分布，可以得到，

\[ q^{\prime \prime}=\frac{\Gamma_{12}}{v_{l 1}^{2}} \frac{k_{\mathrm{B}}^{4}}{8 \pi^{2} \hbar^{3}}\left(T_{1}^{4} \int_{0}^{x_{\mathrm{m}, 1}} \frac{x^{3} \mathrm{~d} x}{\mathrm{e}^{x}-1}-T_{2}^{4} \int_{0}^{x_{\mathrm{m}}, 2} \frac{x^{3} \mathrm{~d} x}{\mathrm{e}^{x}-1}\right) \]

\(x\)是无量纲的能量，

\[ x = \frac{\hbar\omega}{k_BT} \]

在低温极限下，由于，

\[ \int_{0}^{\infty} \frac{x^3}{e^x - 1} \mathrm{d}x = \frac{1}{15}\pi^4 \]

于是，

\[ q^{\prime \prime}=\frac{\Gamma_{12}}{v_{l 1}^{2}} \frac{\pi^{2} k_{\mathrm{B}}^{4}}{120 \hbar^{3}}(T_1^4 - T_2^4) \]

把\(v_{l1}^{-2}\)用\(\sum_j v_{j1}^{-2}\)替代，可以得到，

\[ q^{\prime \prime}=\Gamma_{12} \frac{\pi^{2} k_{\mathrm{B}}^{4}}{120 \hbar^{3}}(T_1^4 - T_2^4)\sum_j v_{j1}^{-2} \]

TBR可以计算了，

\[ \begin{aligned} R_b^{\prime\prime} &= (T_1 - T_2) / q^{\prime\prime} \\ &= \frac{120 \hbar^{3}(T_1 - T_2)}{\Gamma_{12} \pi^{2} k_{\mathrm{B}}^{4}(T_1^4 - T_2^4)\sum_j v_{j1}^{-2}} \\ &= \frac{120 \hbar^{3}}{\Gamma_{12} \pi^{2} k_{\mathrm{B}}^{4}(T_1^2 + T_2^2)(T_1 + T_2)\sum_j v_{j1}^{-2}} \\ &\approx \frac{30 \hbar^{3} T^{-3}}{\Gamma_{12} \pi^{2} k_{\mathrm{B}}^{4}\sum_j v_{j1}^{-2}} \end{aligned} \]

AMM模型只有在声子波长远大于界面粗糙度时才近似成立，在实际应用中是基本不成立的。

DMM模型假设声子在入射到界面后将失去它初始状态的记忆，以一定概率散射到两种介质中，因此两介质中的穿透概率和反射概率是倒易的， \[ \begin{aligned} \Gamma_{12} + R_{12} &= 1 \\ R_{12} &= \Gamma_{21} \end{aligned} \] 于是 \[ \Gamma_{12} + \Gamma_{21} = 1 \] 由于 \[ \Gamma_{21} = \frac{\sum v_{i2}^2}{\sum v_{i1}^2}\Gamma_{12} \] 因此 \[ \Gamma_{12}=\frac{\sum_{j} v_{j 2}^{-2}}{\sum_{j} v_{j 1}^{-2}+\sum_{j} v_{j 2}^{-2}} \] 不同对DMM模型做的改进基本上是修改透射系数的形式，比如， \[ \tau_{12}=\frac{\sum_{j} \int_{0}^{\omega_{m}} \hbar \cdot \omega \cdot v_{2, j} \cdot f_{B E} \cdot D(\omega) d \omega}{\sum_{j} \int_{0}^{\omega_{m}} \hbar \cdot \omega \cdot v_{1, j} \cdot f_{\mathrm{BE}} \cdot D(\omega) d \omega+\sum_{j} \int_{0}^{\omega_{m}} \hbar \cdot \omega \cdot v_{2, j} \cdot f_{\mathrm{BE}} \cdot D(\omega) d \omega} \] 热流的计算公式并不发生改变.

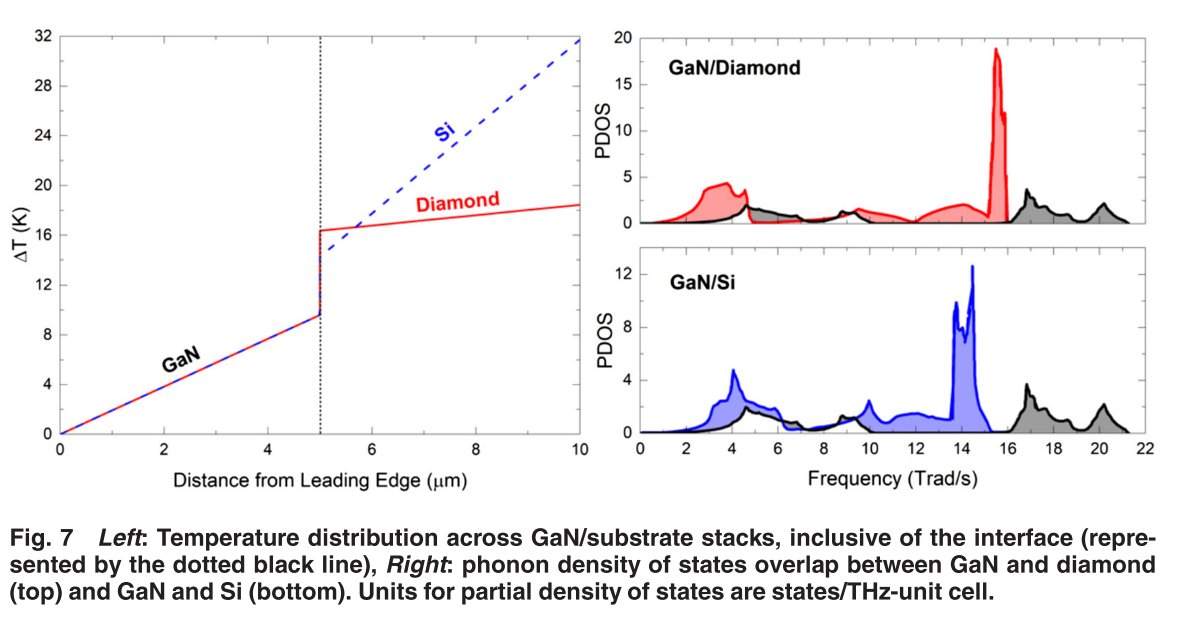
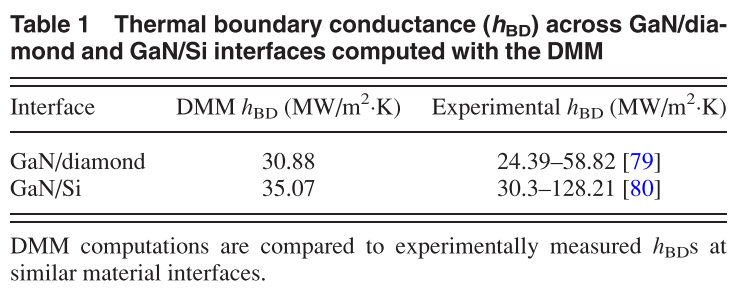
TBR是个非常复杂的问题，实验测量的不确定度很高。当两层材料的声子态密度重合区域很小时，根据DMM模型预测发生声子透射的概率很小，也导致了界面热导非常低，此时界面发生的温度跳跃也就非常显著。