GaN-HEMT的双热源模型

Chen X, Boumaiza S, Wei L. Modeling Bias Dependence of Self-Heating in GaN HEMTs Using Two Heat Sources[J]. IEEE Transactions on Electron Devices, 2020, 67(8): 3082-3087.

感觉是很适合和之前的工作结合的一个工作，这个工作的出发点是已有的单纯的热模型是没法考虑bias dependence的，而考虑bias dependence需要较为复杂的电热联合模拟. 同时，即使基于傅里叶定律，目前还没有关于对GaN-HEMT自热的bias dependence定量的研究. 作者提出了一个简单的双热源模型，可以通过单纯的热仿真来模拟不同bias下的温度场及结温的差异情况，模型可以适用于不同栅极-漏极-源极长度以及不同GaN厚度的情况. 这个模型需要器件的输出曲线作为输入.

双热源模型

这个工作最初的想法大概是GaN-HEMT channel中的产热分布呈现出一个明显的尖峰，除了Gate下面靠近Drain的一侧有一个尖峰外，其余部分基本都是低水平的均匀分布.

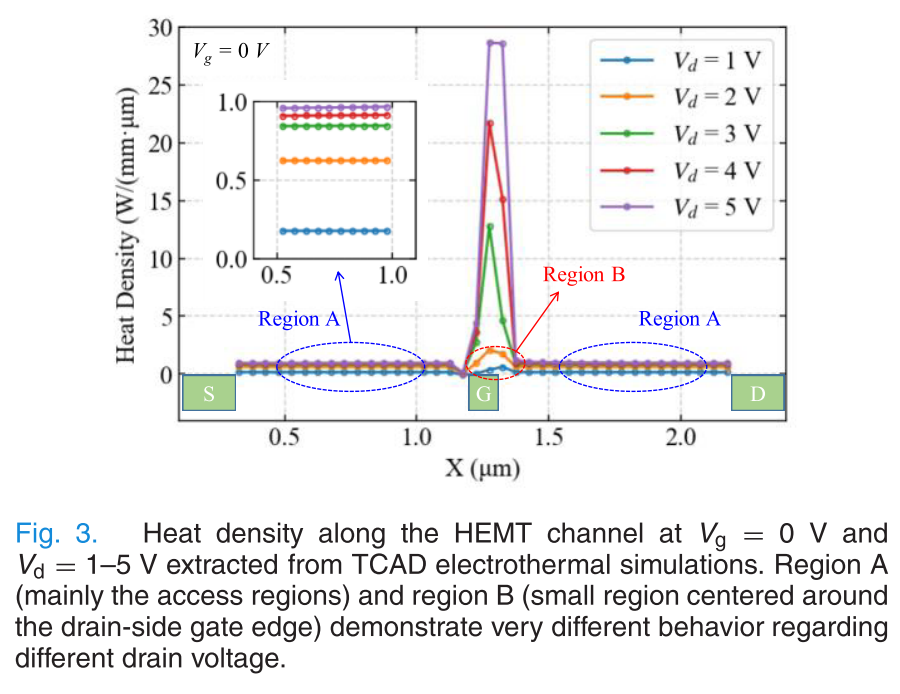
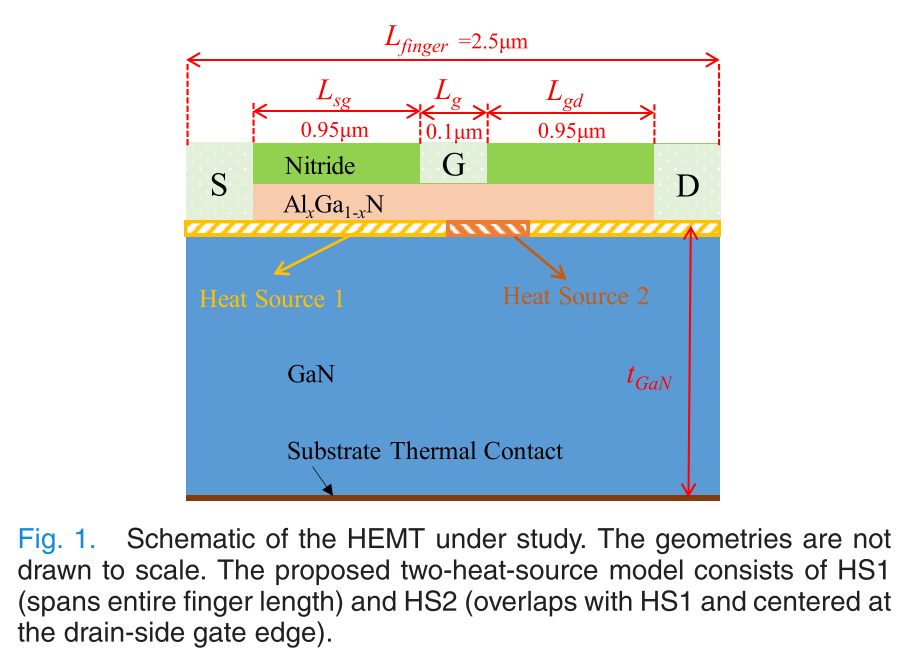
于是作者把沟道内的产热划分为两个区，每个区内都是均匀产热，HS1覆盖了整个沟道区域，用来反映均匀产热；HS2的中心设置在栅极靠近漏极一侧的边缘，宽度设置为0.16微米，用来描述产热的集中分布. 后面的讨论可以看到，HS2的宽度与栅极宽度基本无关，这个0.16微米适用于各种宽度的栅极.

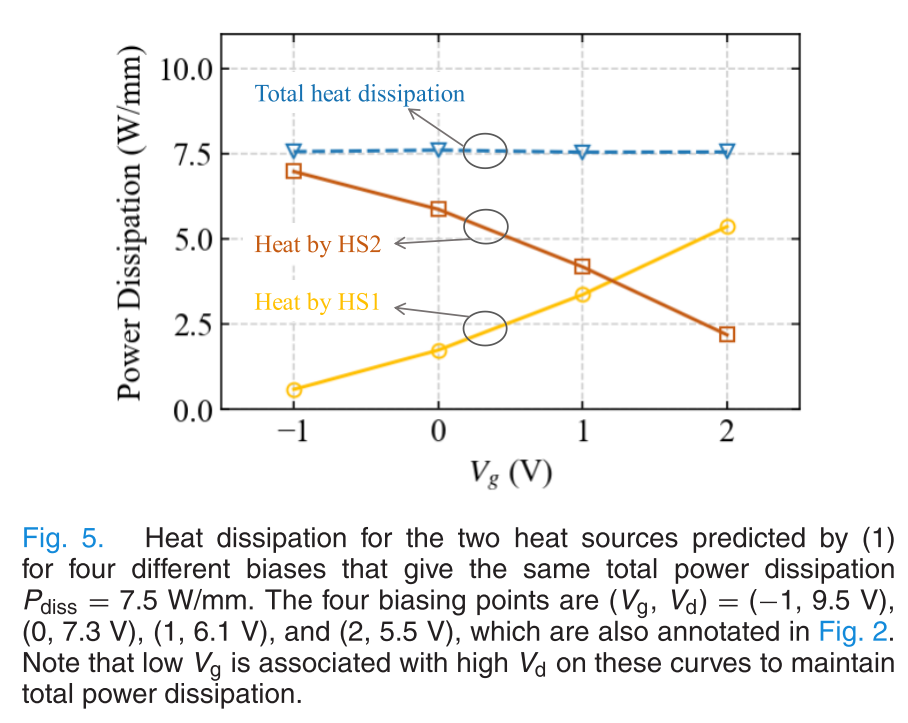
下面这张图是在\(V_g=0\,\mathrm{V}\)时这两个区产热的情况，在\(V_d<2.2\, \mathrm{V}\)时，HS2的产热量基本为0，而HS1的产热量随着\(V_d\)线性增长；而在\(V_d>2.2\,\mathrm{V}\)后，HS1的产热量基本保持不变，此时增加的产热基本是由HS2贡献的，且HS2的产热随着\(V_d\)的增长而线性增长.

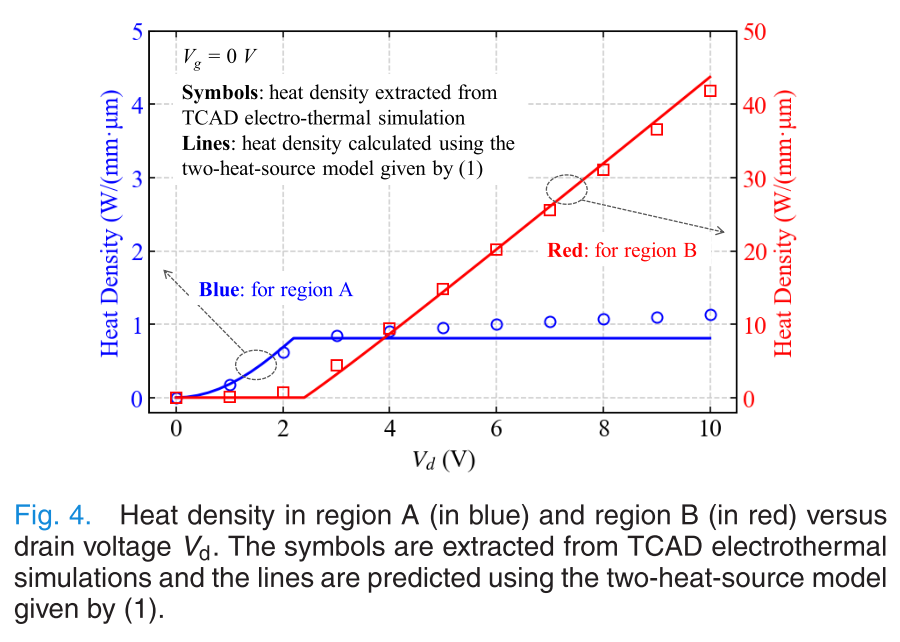
实际上这个\(2.2\,\mathrm{V}\)就是\(V_d=0\,\mathrm{V}\)时的饱和电压.

于是这个双热源模型可以整理成 \[ \begin{cases}P_{1}=I_{\mathrm{d}} V_{\mathrm{d}}, \quad P_{2}=0, & \text { for } V_{\mathrm{d}} \leq V_{\mathrm{dsat}} \\ P_{1}=I_{\mathrm{d}} V_{\mathrm{dsat}}, \quad P_{2}=I_{\mathrm{d}}\left(V_{\mathrm{d}}-V_{\mathrm{dsat}}\right), & \text { for } V_{\mathrm{d}}>V_{\mathrm{dsat}}\end{cases} \] 当\(V_d\)小于饱和电压的时候，此时总功率完全等于HS1的发热量；当\(V_d\)大于饱和电压的时候，HS1的发热量保持不变，此时剩下增长的功率都放在HS2的发热上. 所以可以看到，在总功耗一样的情况下，栅极越负，则器件需要更大的漏极电压才能维持同样的功率，产热就越发集中，此时HS2占据的总发热量就越大，导致结温就越高，这就是\(T_{max}\) bias dependence的基本图像.

模型验证

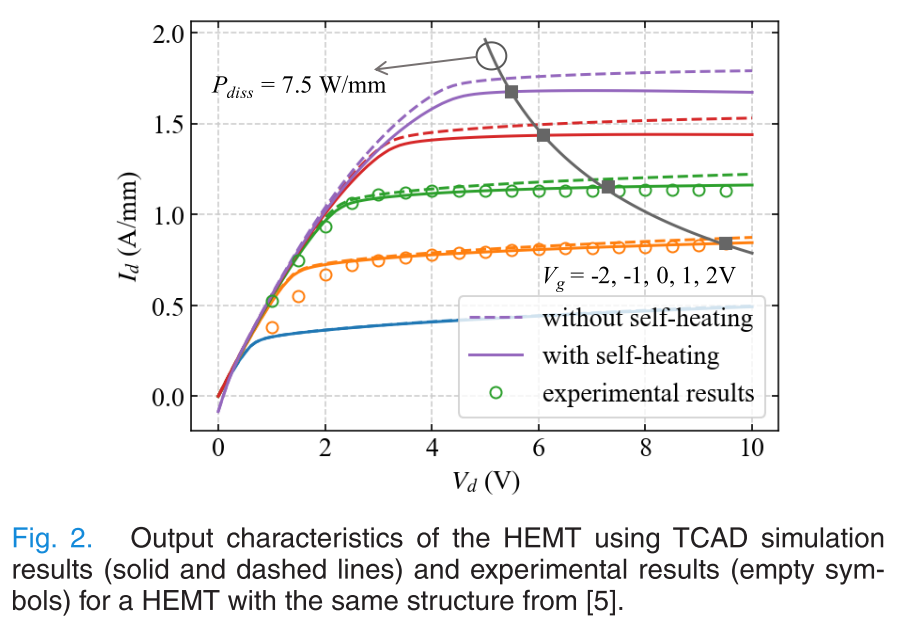
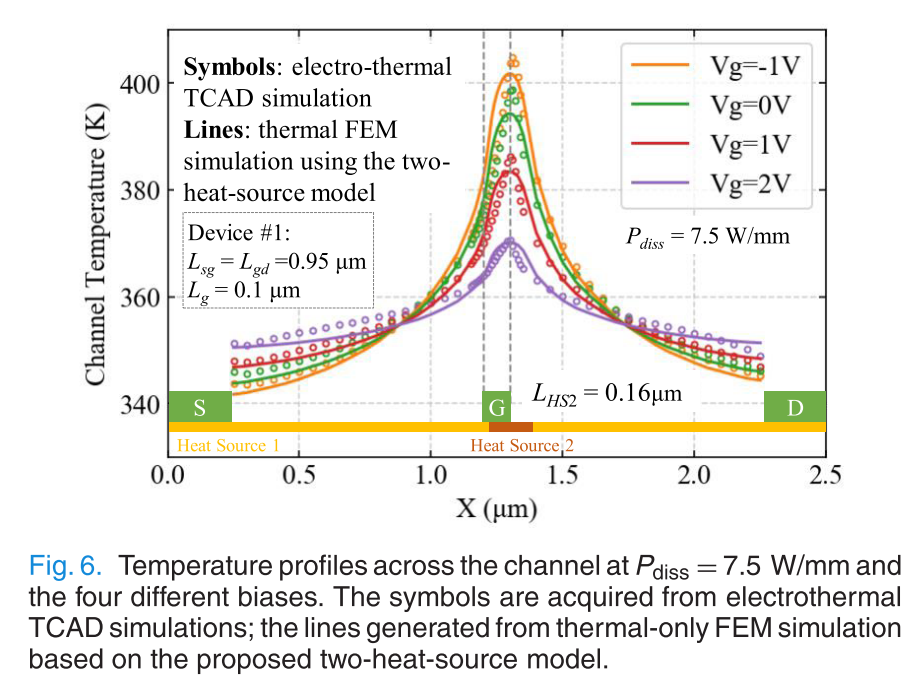
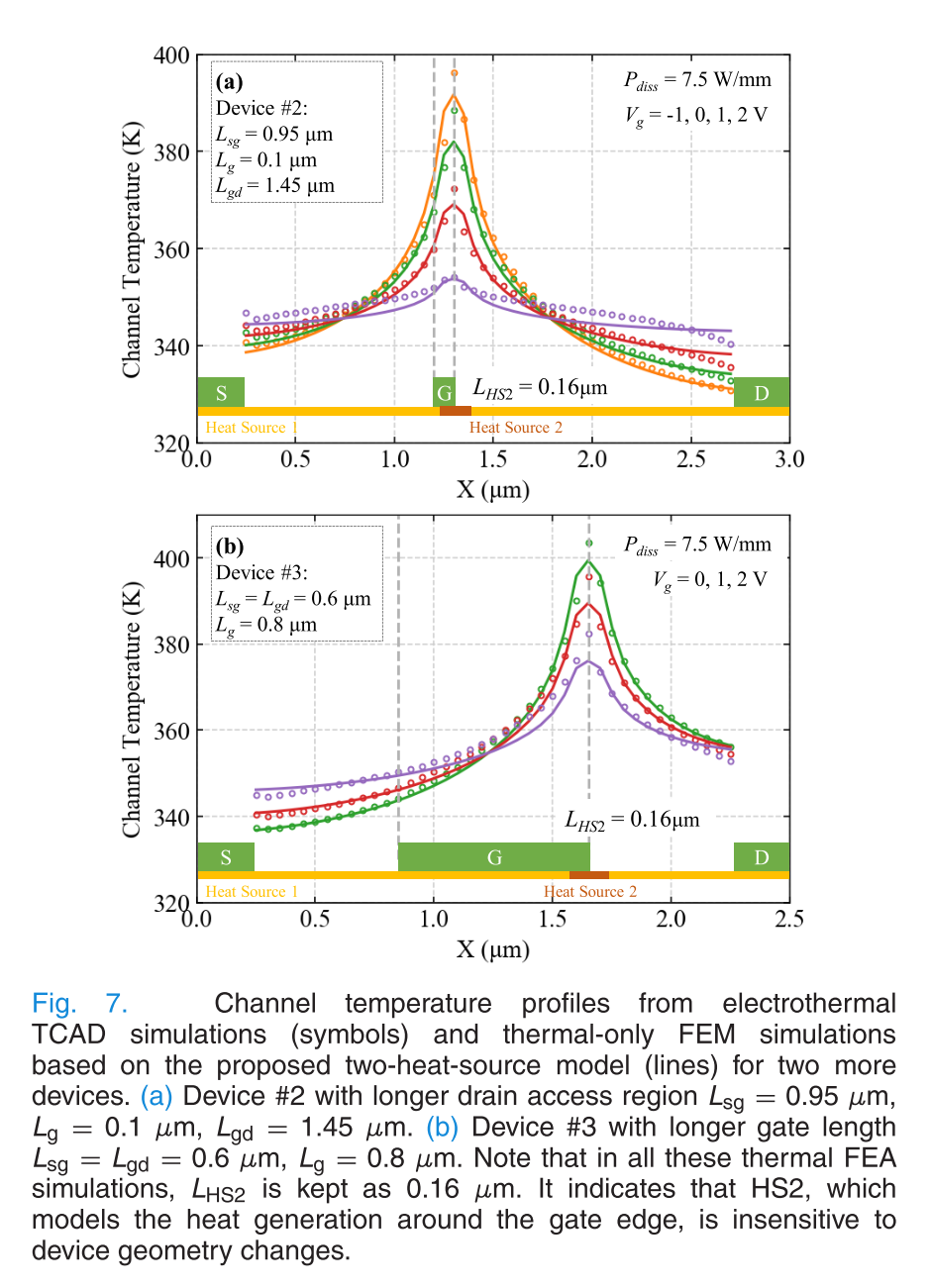
作者比较了几种不同layout的器件，不同的bias下电热耦合仿真以及双热源模型得到的温度场，一致性都很好. 当然作者也说了，很难用实验去验证，MicroRaman的分辨率只有500nm，而红外的分辨率只有3微米，这些设备测出的结温都要比模拟低很多，因此这种\(T_{max}\) bias dependence的实验结果也非常小，模拟值统一功耗不同bias差出了35K，实验值可能只有10K，要测出非傅里叶效应.. 那就更加困难了，因为它更加集中在热点的一小块范围内.

基于双热源模型的热阻模型

\[ T_{\text{max}} = T_0 + (R_{\text{sub}}+R_1)P_1 + (R_{\text{sub}}+R_2)P_2 \]

\(R_1\)和\(R_2\)分别是HS1和HS2的热阻，\(R_{\text{sub}}\)是GaN buffer layer和衬底间的界面热阻. \(R_1\)相当于表面均匀热源发热，可以用一维热阻近似计算， \[ R_1 = t_{\text{GaN}}/(k_{\text{GaN}}L_{\text{finger}}W_{\text{finger}}) \] \(R_2\)就是熟悉的扩展热阻了，可以用无穷级数或者有限元去计算. \[ \frac{Q}{a}\frac{t_{1}}{k_{1}}+\sum_{n=1}^{\infty} \frac{8 Q \sin ^{2}\left(\frac{c \lambda_{n}}{2}\right) \cos ^{2}\left(X_{c} \lambda_{n}\right)}{a c^{2} k_{1} \lambda_{n}^{3} \phi_{n}\left(\lambda_{n}\right)} \]