短栅GaN-HEMT中的自热(1)

Chen X, Boumaiza S, Wei L. Self-heating and equivalent channel temperature in short gate length GaN HEMTs[J]. IEEE transactions on electron devices, 2019, 66(9): 3748-3755.

（感谢陈雪松师兄发给我器件的input文件）

自热效应被定义为器件在高电压、大电流的应用条件下，沟道处产生的热量使晶格温度升高，引起器件特性退化的效应. 在大多数关于自热退化的模型中，用到的温度都是器件最高温度\(T_{\text{max}}\). 作者这篇文章的主要结论就是用\(T_{\text{max}}\)并不是完全合理的，尤其是在短栅的HEMT中. 作者提出了等效沟道温度的概念来衡量自热效应，通过对沟道分区，对这个结论给出了一个物理上的直观的解释，这个分区还挺有意思的.

Simulation Setup

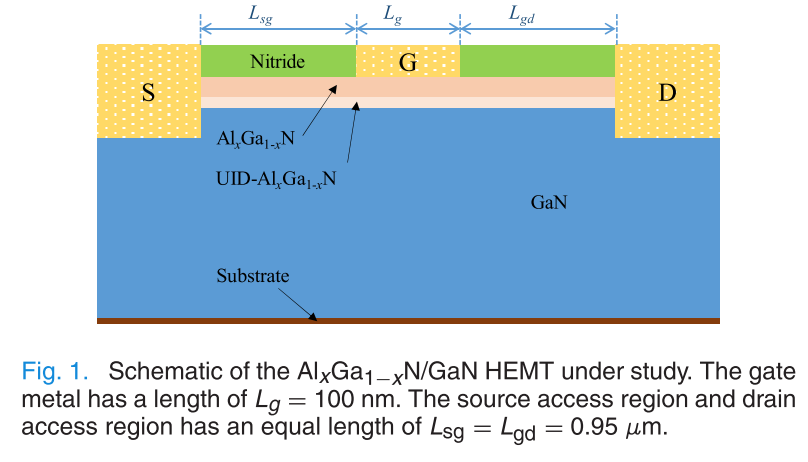
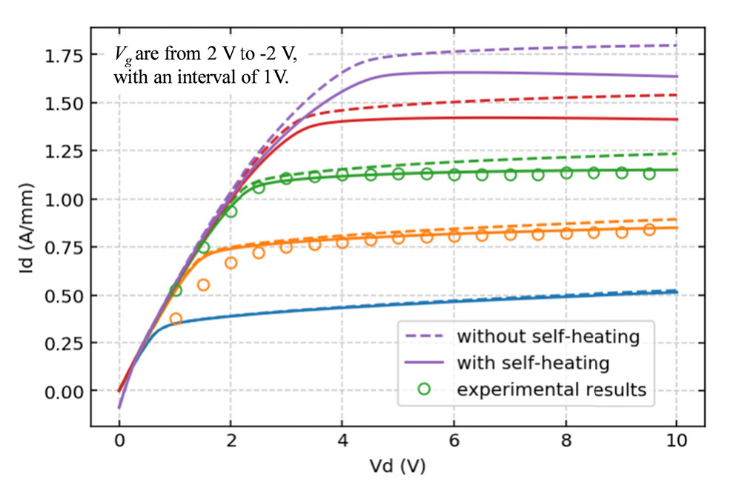
作者模拟的是这样一个GaN HEMT结构，栅长100nm，氮化镓层厚度1um，底部衬底接触设置为第三类边界条件，\(T=300\,\mathrm{K}, h_c = 0.5\times 10^{-8}\, \mathrm{W/m^2K}\). 分别在开启自热（求解温度场）和不开启自热（假设器件等温）的条件下扫了器件的输出曲线，开启自热后器件的输出电流肯定要低于不开启自热的情况.

等效沟道温度

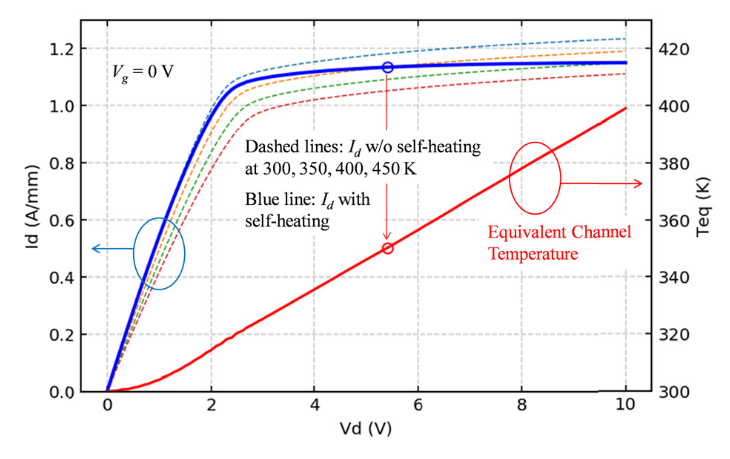
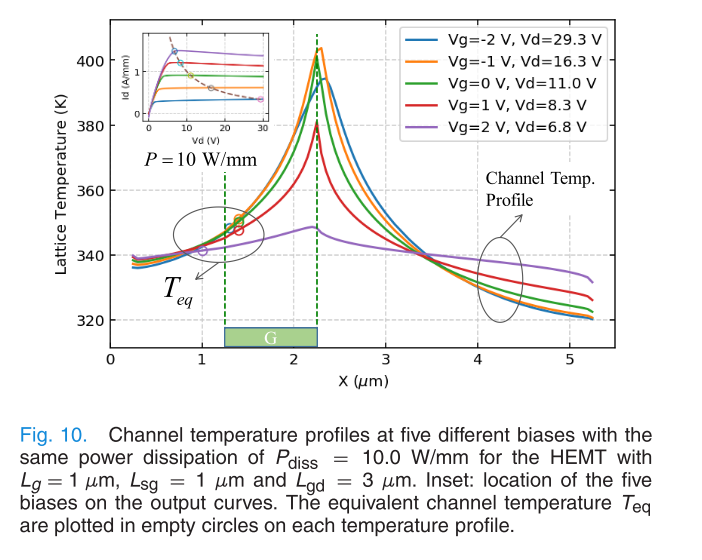
作者这样定义等效沟道温度， \[ T_{\mathrm{eq}}\left(V_{\mathrm{GS}}, V_{\mathrm{DS}}\right)=\left.T_{\mathrm{uniform}}\left(V_{\mathrm{GS}}, V_{\mathrm{DS}}\right)\right|_{@} I_{\mathrm{DS}, \text { self-heating }}=I_{\mathrm{DS}, \text { uniform }} \] 比如300K等温不开启自热时得到的电流为1.0，开启自热后得到的电流为0.9，此时我可以将器件的等效温度设置为350K，不开启自热去计算，得到的电流就变成了0.9，就称350K为这个\(V_{G}, V_D\) bias下的等效温度. 要是光拟合这条线就没什么意思了，但是后面的解释还是挺有趣的.

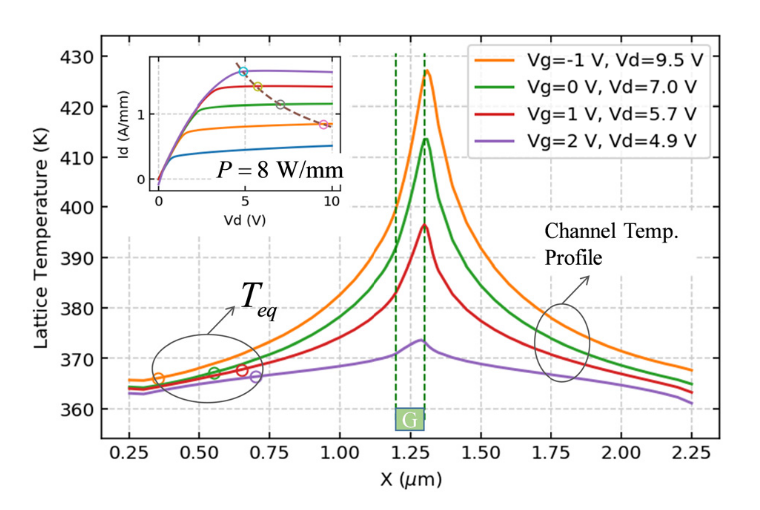
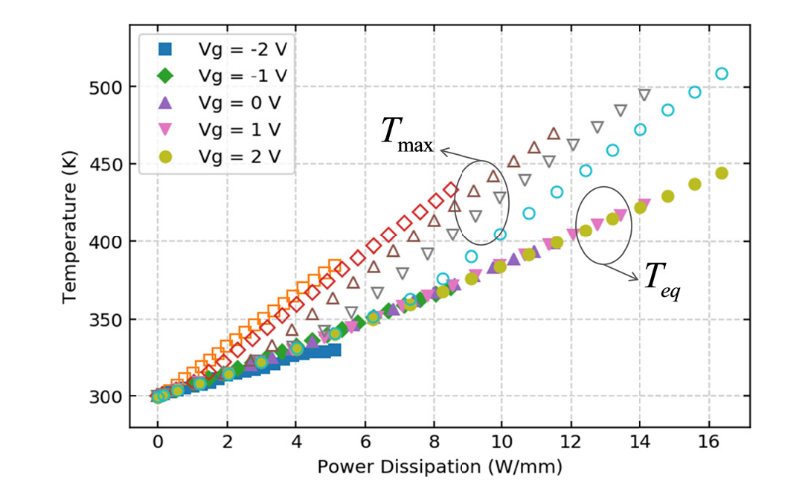
上面这张图是在功耗为\(8\, \mathrm{W/mm}\)时（实际计算的是器件的2D切面，电流和功耗都跟器件垂直纸面的长度成正比，现实也是如此. 因此为了衡量功耗的大小，采用\(\mathrm{W/mm}\)这样的单位，它衡量了一个切面的功耗. ）不同bias条件下的沟道内温度分布及其等效温度. 在功耗相同时，不同的bias下最高温度可以相差50K，因为\(V_d\)越大的时候，器件的饱和程度越大，此时产热也就更加集中. 而在总功耗一致的情况下，\(T_{eq}\)基本与bias无关. 下面这张图展示了不同\(V_g\)下\(T_{max}\)和\(T_{eq}\)随总功耗的变化，\(T_{max}\)显著和\(V_g\)相关，而\(T_{eq}\)基本与\(V_g\)无关，只与总功耗有关. 这个结论并不是显然的.

对结果的解释

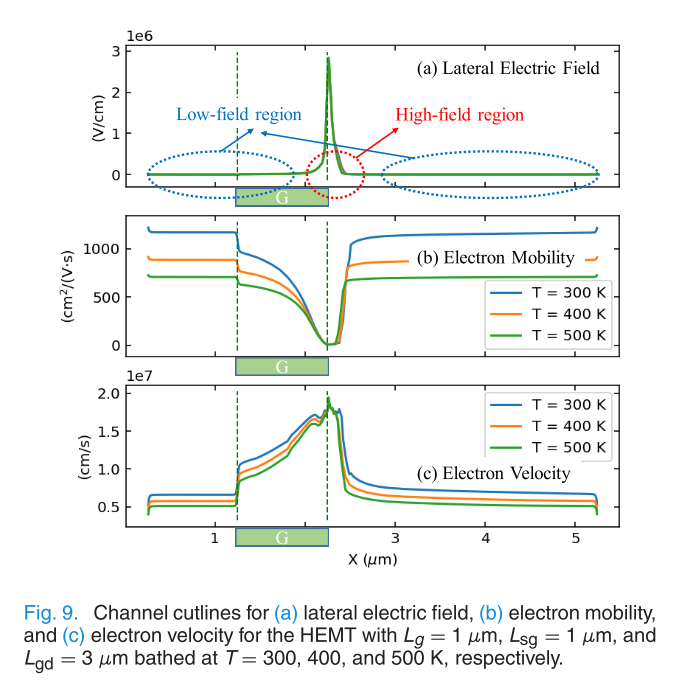
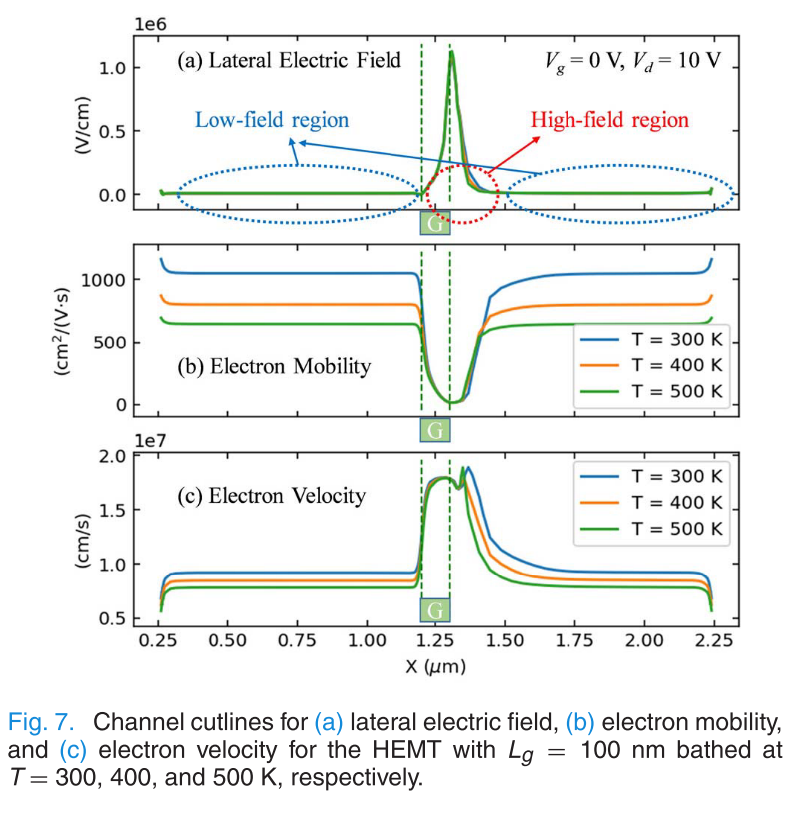
在sheet近似下，即把导电沟道近似成一个面，竖直方向的厚度近似为0，此时导电沟道可以认为是一层二维电子气，即只有x方向和垂直纸面方向两个维度，此时Drain电流可以表示为 \[ I_D(T) = Wqn_S(x,T)v(x,T) \] \(n_S\)为电子面密度，\(v\)为电子沿沟道的漂移速度，\(W\)是垂直纸面方向的沟道宽度，\(q\)是电子的电荷量. 其中\(n_s\)的温度依赖性主要体现在三个参数上，AlGaN/GaN界面处的带隙偏移\(\Delta E_c\)，极化面电荷\(\sigma\)以及费米能级\(E_F\)，而这三个参数的温度依赖性都很弱. 而漂移速度同时受到温度和电场影响，由于GaN HEMT通常在高压下工作，沟道内的电场强度非常大，因此速度饱和效应非常明显. 在GaN HEMT中通常采用的漂移速度公式为 \[ v(E, T)= \begin{cases}\frac{\mu_{0}(T) E}{1+a E / E_{C}(T)}, & E<E_{C}(T) \\ v_{\text {sat }}(T), & E>E_{C}(T)\end{cases} \] \(\mu_0(T)\)是在低场下的迁移率，\(E_C(T)\)是临界场强，超过临界场强后，电子的速度达到饱和，饱和速度的温度依赖性较弱. 低场迁移率\(\mu_0\)主要受到两个散射机制影响，声子散射以及杂质散射. 由于GaN的掺杂浓度不高，迁移率由声子散射主导，温度越高，声子散射越强，迁移率越低，此时迁移率可以近似为， \[ \mu_{0}(T)=\mu_{0}\left(T_{0}\right)\left(\frac{T}{T_{0}}\right)^{-\alpha} \] 于是漂移速度可以进一步简化为 \[ v(E, T)= \begin{cases}\mu_{0}\left(T_{0}\right)\left(\frac{T}{T_{0}}\right)^{-\alpha} & E, \quad \text { low-field } \\ v_{\text {sat }}, & \text { high-field }\end{cases} \] 下面这张图是分别在300K，400K和500K的沟道内电场、电子迁移率以及电子速度的分布，对于工作在饱和区的HEMT，主要的电压降低集中在Gate靠近Drain的一侧，因此场强仅在该处形成了一个spike，而剩下的部分都是低场区域. 从结果来看，对于短栅的HEMT，电子速度在栅靠近源的一侧迅速上升，并且在栅的边缘处基本就达到饱和，高场区域覆盖了栅极下方全部以及靠近漏极的一部分，而由于高场区域电子速度基本饱和，受温度影响的程度很弱，而低场区域电子的速度没有达到饱和，因此其速度显著受到温度的影响.

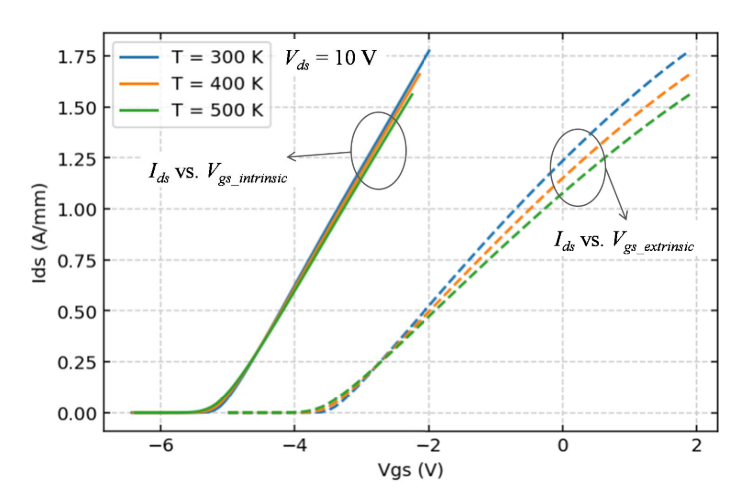
所以从上面的讨论可以得到短栅HEMT温度敏感性的图像，对于高场下的gated区域，基本不受温度影响，而低场下的区域显著受到温度影响，温度越高，电子运动的阻力就越大，运动速度也就越小. 但要注意这些结论的假设，DDM+漂移速度模型，没有考虑任何电子非平衡输运，不过从文章的介绍来看应该不会产生什么定性影响. 所以从channel内等效温度的分布可以看出，等效温度位于source区域某个远离热点的位置，因为上面的分析表明自热引起的温升并不怎么影响栅极下的高场区域，而主要是增加了低场区域电子运动的阻力. 下面这张图中的\(V_{gs,\text{intrinsic}}\)指的是gate和source一侧gate边缘之间的电压，\(v_{gs,\text{extrinsic}}\)指的就是gate和source之间的电压，温度对\(V_{gs,\text{intrinsic}}\)基本没有影响，而\(v_{gs,\text{extrinsic}}\)显著受到温度的影响，而这就是自热效应的宏观体现了.

栅长的影响

从上面不同温度下短栅沟道内电子速度的分布可以看到，对于100nm栅长的情况由于gate下面的场强非常大，电子的漂移速度迅速达到饱和，此时温度对于高场区饱和漂移速度影响不大. 而在栅长为1微米的时候，此时gate下面的电势变化就变缓了，电场强度也就不那么大，下图是\(v_g=0\, \mathrm{V}, v_d = 30 \, \mathrm{V}\)时1微米栅宽HEMT沟道内的电子迁移率和电子漂移速度的分布情况. 此时不存在一个明显的饱和区了，因此此时即使是等效温度也并不完全是功率的单值函数了，在同一功率下，\(T_{eq}\)的差距也达到了10K. 但它的bias相关性还是要显著弱于\(T_{max}\)的bias依赖.