MD能量与压强

MD能量与压强计算

对关联函数\(g(r)\)

\(256Ar，\rho=0.75, T = 1.0\)，对关联函数：

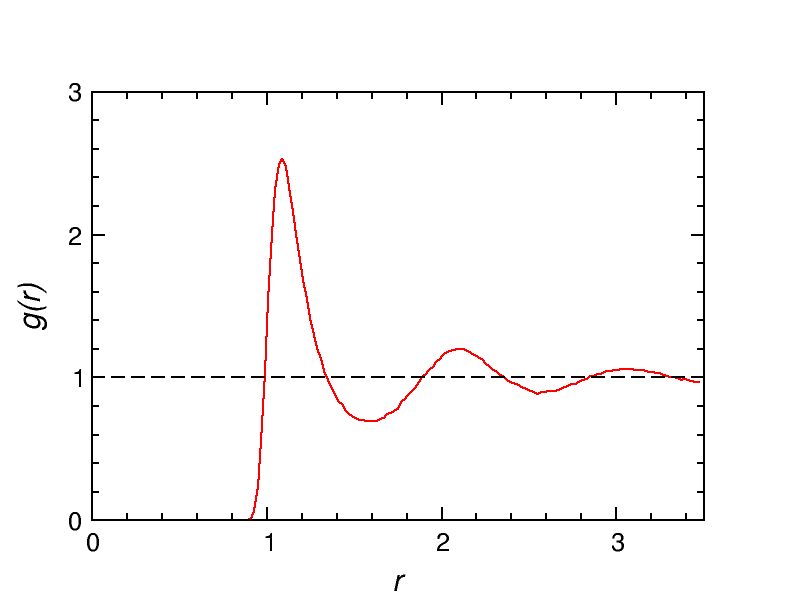
对关联函数是粒子之间与时间无关的关联性的量度，\(g(r)\)用以描述粒子数密度作为距参考原子的距离的函数如何变化。 \[ g(r) = \frac{n(r)}{4\pi r^2 dr}/(\frac{N}{V}) = \frac{n(r)}{4\pi r^2 dr}/\rho \quad(\rho=N/V) \] \(n(r)\)为\(r\sim r+\mathrm{d}r\)范围内的平均粒子数，\(\rho g(r)\)就是r处的粒子数密度。对关联函数在分子模拟中很有用，一方面，它揭示了流体结构以及分布的信息；另一方面，一个系统中任何pair function的系综平均都可以用\(\rho g(r)\)作为权重来对空间积分以求均值，对一个各向同性的流体系统： \[ \left<\mathscr{A}\right> = \left< \sum_i\sum_{j>i} a(r_{ij}) \right> = \frac{1}{2}N \int_0^\infty a(r)\rho g(r)4\pi r^2\mathrm{d}r \] 其中\(1/2\)由于两个原子相互作用积分多算了一次。

Virial theorem 维里定理

考虑一个大量质点（N）的体系，质点的位矢\(r\)和动量\(p\)两者均有界，并将此体系所有质点的位矢和动量的标量积之和用\(S\)表示： \[ S=\sum_{i=1}^{N} r_{i} \cdot p_{i} \] 将上式对时间求导： \[ \frac{d S}{d t}=\sum_{i=1}^{N}\left(\dot{r}_{i} \cdot p_{i}+r_{i} \cdot \dot{p}_{i}\right) \] 取系统的时间平均： \[ \left\langle\frac{d S}{d t}\right\rangle=\frac{1}{\tau} \int_{0}^{\tau} \frac{d S}{d t} d t=\frac{S(\tau)-S(0)}{\tau} \] 体系由大量粒子组成，在足够长的时间过后，必然有： \[ S(\tau)-S(0)=0 \quad \Rightarrow \quad\left\langle\frac{d S}{d t}\right\rangle=0 \] 于是： \[ \left\langle\sum_{i=1}^{N}\left(\dot{r}_{i} \cdot p_{i}\right)\right\rangle=-\left\langle\sum_{i=1}^{N}\left(r_{i} \cdot \dot{p}_{i}\right)\right\rangle \] 方程的左侧是体系动能的2倍，右侧是各粒子位矢和受力的标量积之和，于是： \[ \langle K\rangle=-\frac{1}{2}\left\langle\sum_{i=1}^{N}\left(r_{i} \cdot F_{i}\right)\right\rangle \] 得到维里定理：

由无数指点组成的力学体系，体系总动能的平均值等于其均功（维里）的负值。

把体系中各粒子位矢和受力标量积的一半，称作体系的维里。

把维里定理左右两边分别展开： \[ \frac{3}{2}Nk_BT = -\frac{1}{2}\left\langle\sum_{i=1}^{N}\left(r_{i} \cdot \left(F_{intermolecular}+F_{e}\right)\right)\right\rangle \] 其中粒子所受的外力等值于对外墙的碰撞：\(F_e = -P\vec{n}\mathrm{d}S\)

于是外力的均功为： \[ \begin{aligned} \Xi_{e}&=\frac{1}{2}\left\langle\sum_{S}\left(\vec{r} \cdot \vec{F}_{e}\right)\right\rangle \\ &=-\frac{1}{2} \oiint_{S} P(\vec{r} \cdot \vec{n}) d S \\ &=-\frac{1}{2} P \iiint_{V}\left(\frac{\partial}{\partial \vec{r}} \cdot \vec{r}\right) d \vec{r}\\ &=-\frac{3}{2} P V \end{aligned} \] 分子间相互作用的均功为： \[ \Xi_{i}=\frac{1}{2}\left\langle\sum_{i}\left(r \cdot F_{intermolecular}\right)\right\rangle \] 将其改写为与坐标系无关的形式，其中每一个粒子的受力都是它与其他所有粒子相互作用之和： \[ \sum_i r_i f_i = \sum_i r_i \sum_{j \neq i} f_{ij} = \sum_i\sum_{j \neq i} r_i f_{ij} \] 由于在上式中下标i与j是等价的，且分子之间的作用力是相互的，因此上式可改写成index对称的形式： \[ \sum_i\sum_{j \neq i} r_i f_{ij} = \frac{1}{2}\left( \sum_i\sum_{j \neq i} r_i f_{ij} + r_j f_{ji}\right) \]

其中根据牛顿第三定律，\(f_{ij} = -f_{ji}\)，于是可将内力均功改写成分子间相互作用的形式： \[ \begin{aligned} \sum_i\sum_{j \neq i} r_i f_{ij} &= \frac{1}{2}\left( \sum_i\sum_{j \neq i} r_i f_{ij} + r_j f_{ji}\right) \\ & = \frac{1}{2}\left( \sum_i\sum_{j \neq i} r_i f_{ij} - r_j f_{ij}\right) \\ &= \frac{1}{2}\sum_i\sum_{j\neq i} r_{ij}f_{ij} \end{aligned} \] 于是： \[ \Xi_{i}=\frac{1}{2}\left\langle\sum_{i}\left(r \cdot F_{intermolecular}\right)\right\rangle=-\frac{1}{4}\left\langle\sum_{i}\sum_{j\neq i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)\right\rangle \]

代回维里定理中，得到： \[ \frac{3}{2}Nk_BT = \frac{3}{2}PV + \frac{1}{4}\left\langle\sum_{i}\sum_{j\neq i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)\right\rangle \] 于是压强可表达为： \[ \begin{aligned} P &= \rho k_BT - \frac{\rho}{6N}\left\langle\sum_{i}\sum_{j\neq i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)\right\rangle \\ &= \rho k_BT - \frac{\rho}{3N}\left\langle\sum_{i}\sum_{j > i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)\right\rangle \end{aligned} \] 第二项可用对关联函数\(g(r)\)将求和改写为积分： \[ \left\langle\sum_{i}\sum_{j > i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)\right\rangle =\frac{1}{2N}\int_0^\infty \rho g(r)r\frac{\partial U}{\partial r}\cdot 4\pi r^2 \mathrm{d}r \] 压强可最终表达为： \[ P = \rho k_BT - \frac{\rho^2}{6}\int_0^\infty g(r) \frac{\partial U}{\partial r}\cdot 4\pi r^3 \mathrm{d}r \]

长程修正

能量和压强的一般形式可写为： \[ \begin{aligned} E &= \frac{3}{2}Nk_BT + \frac{1}{2}N\rho \int_0^\infty U(r) g(r)4\pi r^2 \mathrm{d}r\\ P &= \rho k_BT - \frac{\rho^2}{6}\int_0^\infty g(r) \frac{\partial U}{\partial r}\cdot 4\pi r^3 \mathrm{d}r \end{aligned} \] 在实际计算过程中会采用截断，即只考虑\(r_c\)以内粒子间的受力，忽略\(r_c\)以外的粒子间的相互作用，即： \[ \begin{aligned} E_{cut} &= \frac{3}{2}Nk_BT +\left(\sum_{i}\sum_{j > i} U_{ij}\right)_false\\ P_{cut} &= \rho k_BT -\frac{\rho}{3N}\sum_{i}\sum_{j > i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)_{r<r_c} \end{aligned} \] 这会导致能量和压强的计算出现问题，因此必须考虑长程修正，实际上就可以用能量和压强的一般形式推导长程修正的形式，只需从\(r_c\)积分到无穷远距离即可： \[ \begin{aligned} E &= \frac{3}{2}Nk_BT +\left(\sum_{i}\sum_{j > i} U_{ij}\right)_false+\frac{1}{2}N\rho \int_{r_c}^\infty U(r) g(r)4\pi r^2 \mathrm{d}r\\ P &= \rho k_BT -\frac{\rho}{3N}\sum_{i}\sum_{j > i}\left(r_{ij} \cdot \frac{\partial U_{ij}}{\partial r}\right)_{r<r_c} -\frac{\rho^2}{6}\int_{r_c}^\infty g(r) \frac{\partial U}{\partial r}\cdot 4\pi r^3 \mathrm{d}r \end{aligned} \] 从最上方的\(g(r)\)分布曲线可以看出，当\(r\)足够大时，\(g(r)\approx 1\)，因此在长程修正的部分中，\(g(r)\)也一般取1。

对于L-J势能的流体： \[ U(r) = 4\epsilon \left[ (\sigma/r)^{12} - (\sigma/r)^6 \right] \]

\[ \begin{aligned} E_{lrc} &= \frac{1}{2}N\rho \int_{r_c}^\infty U(r) g(r)4\pi r^2 \mathrm{d}r\\ &= \epsilon\left(\frac{8}{9}\pi N \rho^* {r_c^*}^{-9} - \frac{8}{3}\pi N \rho^* {r_c^*}^{-3}\right)\\ P_{lrc} &= -\frac{\rho^2}{6}\int_{r_c}^\infty g(r) \frac{\partial U}{\partial r}\cdot 4\pi r^3 \mathrm{d}r \\ &= \epsilon/\sigma^3\left(\frac{32}{9}\pi {\rho^*}^2 {r_c^*}^{-9} - \frac{16}{3}\pi {\rho^*}^2 {r_c^*}^{-3}\right) \end{aligned} \]

于是： \[ \begin{aligned} E^* &= \frac{3}{2}NT^* +\left(\sum_{i}\sum_{j > i} 4 \left[ (1/r_{ij}^*)^{12} - (1/r_{ij}^*)^6 \right]\right)_false\\ &+\left(\frac{8}{9}\pi N \rho^* {r_c^*}^{-9} - \frac{8}{3}\pi N \rho^* {r_c^*}^{-3}\right)\\ P^* &= \rho^* T^* -\frac{\rho^*}{3N}\sum_{i}\sum_{j > i}48\left[2(1/r_{ij}^*)^{12} - (1/r_{ij}^*)^6\right]_{r<r_c}\\ &+ \left(\frac{32}{9}\pi {\rho^*}^2 {r_c^*}^{-9} - \frac{16}{3}\pi {\rho^*}^2 {r_c^*}^{-3}\right) \end{aligned} \] 实际中L-J势能的流体的能量和压强计算大致就分为这三部分：

• 能量 = 平动动能 + 相互作用势能 + 长程修正
• 压强 = 理想气体部分 + 总维里 + 长程修正