MOS管的简单IV特性

Essentials of MOSFETs, Mark Lundstrom

我们可以用charge sheet approximation对MOSFET的IV特性做出一些简单又直观的描述，假如我们的MOS管是这样的，

我们认为电流只存在于硅的表面很薄的一层，把这个二维的分布变成一维的分布，那么电流就可以表达成 \[ I_D = - W Q_n(x) \langle v_x(x) \rangle \] \(W\)就是这个sheet的厚度，\(Q_n(x)\)是电荷密度，\(v_x(x)\)是电荷运动速度。电荷密度小的地方，电子运动速度就要快一些，保证每个截面上的电流都是一样的，像是一个变截面面积管道中水的流动。那么我们怎么理解沟道内会出现电荷呢？因为金属-氧化物-半导体MOS结构相当于一个电容，也就是栅的位置，施加栅压后就会诱导出电荷。再上方的能带图里，我们定义能带沿\(x\)变化为0的点为virtual source，虚源，这一点的能带高度只由栅极电压控制，与漏极电压无关，于是这一点的电荷量就可以很简单地表示为 \[ Q_n(x = 0) \approx - C_{ox}(V_{GS} - V_T) \] 其中\(V_T\)是阈值电压，只有超过阈值电压的部分才能使得半导体表面累积可移动的载流子电荷。所以电荷沿沟道分布的基本图像就是，在虚源处由栅压诱导出电荷，这一点的电荷量最大。随着逐渐向漏极移动，沟道内的电压愈发向漏极电压靠近，此时栅压和沟道电压之间的差变小，电荷量逐渐减小，载流子运动速度逐渐增大。

因为\(I_D\)在各个位置都是一样的，所以我们只要知道了一个点的电荷和速度就可以了。由于虚源处的电荷总能够写成上面的形式，因此我们只要知道虚源处的载流子速度就可以了。

Low \(V_{DS}\)

在低场下，载流子速度可以表示成 \[ v_x = - \mu E_x \] 其中\(\mu\)是电子迁移率，\(E_x\)是电场强度，当\(V_{DS}\)比较低时，我们可以认为沟道内的场强比较均匀，就是 \[ E_x = - V_{DS} / L \] 其中\(L\)是沟道长度。于是电流就可以表示成 \[ I_D = \frac{W}{L} C_{ox} (V_{GS} - V_T) \mu V_{DS} \]

High \(V_{DS}\)

Long Channel

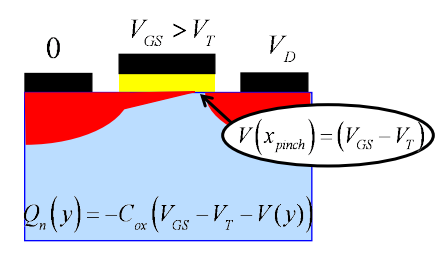
我们知道向漏极靠近的过程中，由漏极电压的影响栅压和沟道电压的差别越来越小。当漏极电压足够大时，会存在一个点使得沟道电压和栅压相等。在这个点，电荷量几乎为零，导致电子速度非常大，我们称这种状况为pinch-off。在pinch-off区域，电场强度非常大，载流子速度也非常大。pinch-off区域的电压为\(V_{GS} - V_T\)，我们近似认为这个区域靠近沟道的边缘，于是电场强度就可以近似表示为 \[ E_x \approx - V(x_{pinch}) / L = - (V_{GS} - V_T) / L \] 此时电流就可以表示成 \[ I_D = \frac{W}{2L}C_{ox}(V_{GS} - V_T)^2 \mu \]

Short Channel

对于短沟道MOSFET，沟道内的电场非常大，如果电势差是1V，沟道长度为20纳米，那么沟道内的场强大概就是\(5\times 10^5 \,\mathrm{V/cm}\)，在这种强度的电场下，整个沟道内的电子速度几乎都已经饱和，于是电子速度可以表示成 \[ v_x = v_{sat} \] 于是 \[ I_D = W C_{ox} (V_{GS} - V_T) v_{sat} \]