理解色散 - A Monte Carlo View

理解色散（能量动量关系）对载流子运动影响的关键就是，是色散决定了载流子波如何运动，而不是载流子的运动决定了他的波有什么样子的色散. 所以在这种意义上，是因为真空中自由电子波具有抛物型的能量动量关系，所以自由电子的运动才符合经典图像中的牛顿第二定律，而并不是因为自由电子的运动符合牛顿第二定律，它才具有抛物型色散波. 引入德布罗意关系，即粒子的动量、能量和它对应的波的波矢、频率之间的关系以后 \[ \mathbf{p} = \hbar \mathbf{k}, E = \hbar\omega \] 我们已经不需要经典意义上的加速度，我们只有能量和动量关系. 所以我们说Monte Carlo方法是半经典的，粒子的图像是经典的，但粒子应该怎么运动是非经典的.

电子

自由电子

给定自由电子的色散关系， \[ \epsilon = \frac{p^2}{2m} = \frac{(\hbar k)^2}{2m} \] 于是可以得到自由电子的群速度与能量和动量间的关系， \[ v(k) = \frac{1}{\hbar} \frac{\partial \epsilon}{\partial k} = \frac{\partial \epsilon}{\partial p} = \frac{\hbar k}{m} = \frac{p}{m} \] 力影响电子动量， \[ \frac{\mathrm{d}p}{\mathrm{d}t} = F \] 于是得到了经典的加速度和力之间的关系， \[ m\frac{\mathrm{d}v}{\mathrm{d}t} = F \]

Non-parabolic能带

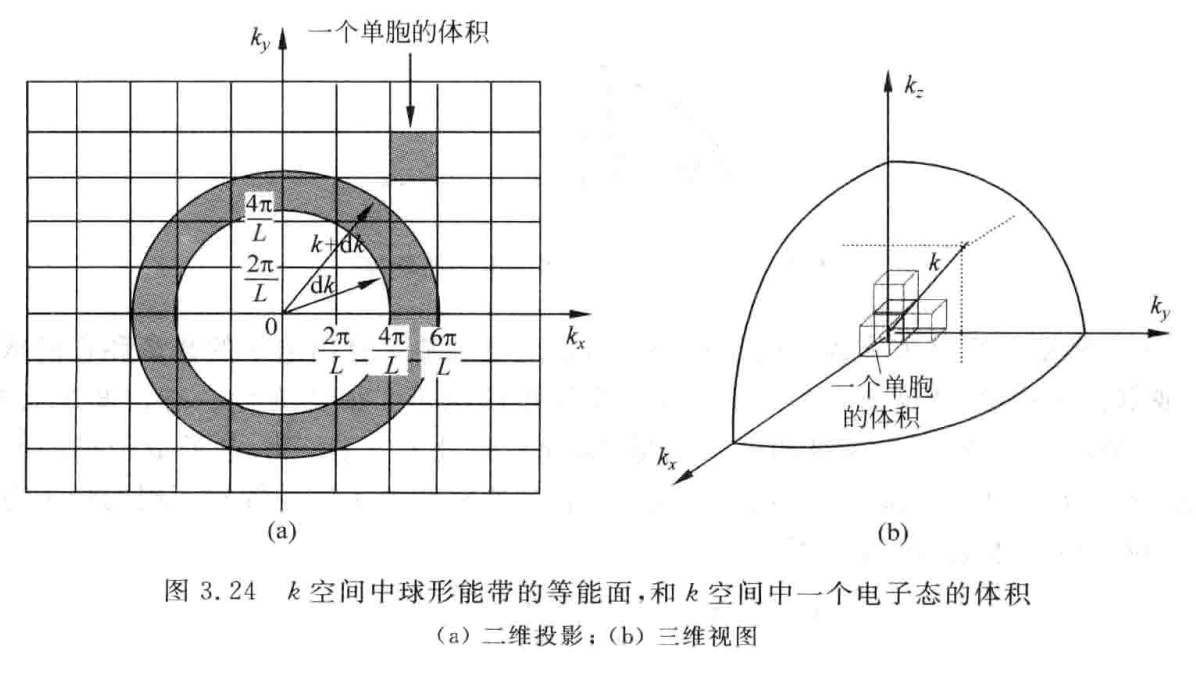
给定实际半导体导带底部non-parabolic的色散， \[ E^s_k (1 + \alpha E^s_k) = \frac{\hbar^2}{2}\left[\frac{(k_x - k^s_{0,x})^2}{m_x^*} + \frac{(k_y - k^s_{0,y})^2}{m_y^*} + \frac{(k_z - k^s_{0,z})^2}{m_z^*}\right] = \gamma \] 其中\(s=1,2,3,4,5,6\)，分别代表6个对称的导带底，我们可以把它改写一下， \[ 2\alpha \epsilon(\mathbf{k}) + 1 = \sqrt{1+4 \alpha \gamma} \] 其中 \[ \frac{\partial \gamma}{\partial k_x} = \hbar^2 \frac{k_x - k^s_{0, x}}{m_x^*} \] 于是可以得到导带里电子波的群速度与它的能量和动量之间的关系， \[ v_x(\mathbf{k}) = \frac{1}{\hbar}\frac{\epsilon(\mathbf{k})}{\partial k_x}=\frac{4\alpha \partial \gamma/\partial k_x}{4 \alpha\sqrt{1+4 \alpha \gamma}} = \hbar \frac{k_x - k^s_{0, x}}{m_x^*\sqrt{1+4 \alpha \gamma}} = \hbar \frac{k_x - k^s_{0, x}}{m_x^* \left(2 \alpha \epsilon(\mathbf{k}) + 1\right)} = \frac{p_x - p^s_{0, x}}{2\alpha\epsilon(\mathbf{k}) + 1} \] 此时电子波的群速度并不是在经典情况下只和动量有关了，而是和动量、能量均有关系. 假如在这个导带底部Valley里的电子受到电场\(\mathbf{E}\)的作用\(\Delta t\)时间，新时刻的电子动量为 \[ \mathbf{p}^{\prime} = \mathbf{p} + \mathbf{E}e\Delta t \] 代入色散关系，即可得到新时刻电子的能量以及群速度了. 在Electron Monte Carlo里，每一个电子在电场中的运动就是按照上述的方式进行的，当然还要处理一下散射过程.

声子

声子色散

声子是不受力的，所以它只有散射引起的扩散过程. 这里讨论一下态密度，态密度这个概念是用来描述能量简并的，就是说有很多个波矢态的能量均为\(E\). 当我们采用各向同性的色散关系时，具有相同能量的波矢态分布在一个球面上. 此时我们确定一个声子的性质时，我们可以只抽取声子的能量（频率），然后乘上该频率（能量）的态密度再乘上该声子态的声子数目（玻色-爱因斯坦分布），就得到了该能量下的声子数目. 由于是各向同性的，我们可以继续在这个球面上抽取波矢方向，相对于对立体角进行抽样. 最后相当于是在球坐标下确定了当前声子的波矢，各向同性假设使得对波矢的大小抽样和方向抽样是解耦的.

当然我们也可以像电子一样，直接抽取波矢，此时就没有态密度这个概念了，当然也就没有立体角这个概念了，因为每个波矢态已经确定了这个声子的所有性质、群速度大小、方向、频率、散射率. 其实这才是最原始的形式，因为量子力学告诉我们这些波矢态本身就是离散的. 这种Monte Carlo模拟，我们可以把它称之为第一性Monte Carlo，第一布里渊区内不同波矢态下声子的频率、群速度、弛豫时间全部用第一性原理算出来，把之前对频率的积分变成对布里渊区里波矢态的离散求和.

比如之前的散射抽样概率为 \[ \frac{\hbar\omega D(\omega)(f_\omega - f_{\omega}^{T_{eq}})\Delta \omega}{\tau(\omega, T_{eq})} / \sum_\omega \frac{\hbar\omega D(\omega)(f_\omega - f_{\omega}^{T_{eq}})\Delta \omega}{\tau(\omega, T_{eq})} \] 现在变成 \[ \frac{\hbar\omega_\mathbf{k} (f_{\omega_{\mathbf{k}}} - f_{\omega_k}^{T_{eq}})}{\tau(\omega, T_{eq})} / \sum_{k_x}\sum_{k_y}\sum_{k_z} \frac{\hbar\omega_\mathbf{k} (f_{\omega_{\mathbf{k}}} - f_{\omega_k}^{T_{eq}})}{\tau(\omega_\mathbf{k}, T_{eq})} \] 热流的话因为各向同性色散是有立体角的概念的，所以之前偏差热流抽样概率为 \[ \begin{aligned} q_{\omega, b}^{\prime \prime}=& \frac{1}{4} \sum_{p} D(\omega, p) v_{g, \omega} \hbar \omega \\ & \times\left(\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{b}}\right)-1}-\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{q q}}\right)-1}\right) \end{aligned} \] 现在回归原始了 \[ q^{\prime\prime}_{\mathbf{k}, b} = \sum_{\mathbf{k}}\hbar\omega (f_{\omega_k} - f_{\omega_k}^{T_{eq}})\vec{v_{g, \mathbf{k}}}\cdot \vec{n} \]

薄膜稳态导热

各向同性sine-shaped色散， \[ \begin{aligned} \omega &= \omega_m\sin(\frac{\pi}{2}\frac{k}{k_m}) \\ k_m &= \frac{\pi}{a_D} = (6\pi^2N)^{1/3} \end{aligned} \] 散射率表达式为 \[ \begin{aligned} \tau^{-1}_I &= A\omega^4 \\ \tau_U^{-1} &= B\omega^2T\exp(-C/T) \\ \tau^{-1} &= \tau^{-1}_I + \tau_U^{-1} \end{aligned} \] GaN的参数 \[ k_m = 10.94\times 10^{9}\, \mathrm{m}^{-1}, \omega_m = 3.5 \times 10^{13}\, \mathrm{rad/s}, A = 5.26\times 10^{-45}\, \mathrm{s^{3}}, B = 1.10\times 10^{-19}\, \mathrm{s/K}, C = 200\,\mathrm{K} \] 正常情况下，因为我们选用了各向同性色散，我们是没有必要在布里渊区里做离散的，因为各个方向都是一样的，我们只需要在这个球的半径方向离散就可以了，这个等价于对频率做离散，于是就引出了态密度这个概念. 那么声子的方向是怎么确定的呢？各向同性就相当于在球面上抽一个方向，对立体角怎么抽样就怎么抽样群速度的方向. 但是当我们在布里渊区里做离散的时候，波矢态的三个分量\(k_x, k_y, k_z\)都是确定的，这个声子的所有运动的性质就都确定了，我们也就没有对立体角抽运动方向这个概念了. 下面这个图，我们在各向同性的布里渊球里随机抽了1000个波矢态，我们模拟的声子所有可能出现的状态，就是这1000个波矢态，每一个态的运动方向也都是固定的.

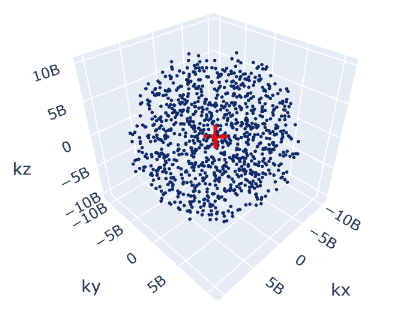
假如我们抽中了波矢态为\((k_x, k_y, k_z)\)的声子，那么它的群速度是多少呢？在各向同性的色散下，群速度只和频率有关， \[ v_g = \frac{\mathrm{d}\omega}{\mathrm{d}k} = \frac{\pi}{2}\frac{\omega_m}{k_m}\cos(\frac{\pi}{2}\frac{k}{k_m}) \] 此时 \[ \begin{aligned} v_{g, x} &= \frac{\mathrm{d}\omega}{\mathrm{d}k_x} = v_g\cdot \frac{k_x}{|\mathbf{k}|}\\ v_{g, y} &= \frac{\mathrm{d}\omega}{\mathrm{d}k_y} = v_g\cdot \frac{k_y}{|\mathbf{k}|}\\ v_{g, z} &= \frac{\mathrm{d}\omega}{\mathrm{d}k_z} = v_g\cdot \frac{k_z}{|\mathbf{k}|}\\ \end{aligned} \] 此时simulation需要选取一个波矢方向，比如我们模拟一个薄膜，这个薄膜摆放是有晶向的，我们可以模拟让\(k_z\)朝上的薄膜一维热传导，此时边界发射的声子态只能够选取\(k_z>0\)的波矢态. 最后统计上也没有什么本质区别，原始各向同性是对波矢空间积分，现在就是对离散波矢态求和了. 对于简单的1D薄膜稳态导热，下面是只发射两万个声子的结果，直接离散布里渊区的情况一般需要更多的声子才能减小统计误差.