蒙特卡洛中的采样

很多算法的需求就是在某个区间\((a, b)\)，按照给定的概率分布函数\(f(x)\)去抽样\(x\)，我们可以从均匀分布出发，来构造这种采样.

直接法

\(f(x)\)在是区间\((a,b)\)内\(x\)的概率分布函数，我们定义\(F(x)\)为\(x\)的累积分布函数，即 \[ F(x_u) = \int_a^{x_u}f(x)\mathrm{d}x \in (0, 1) \]

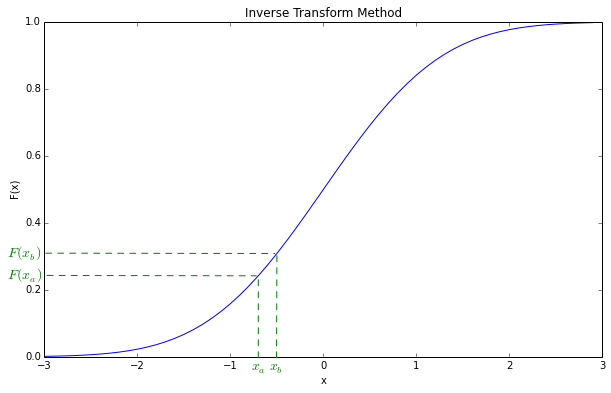
假设我们在\((0, 1)\)中随机均匀采样一个数值\(U\)，即在上图纵轴均匀撒一个点，那么\(U\)落进\((F(x_a), F(x_b))\)之间的概率就是\(F(x_b) - F(x_a)\). 由于累积分布函数是单调的，那么这个概率就等于\(x_u\)落入到\((x_a, x_b)\)之间的概率. 而我们知道\(x\)本身满足\(f(x)\)的概率分布，如果按照\(f(x)\)去抽样，那么理论上\(x\)落入到\((x_a, x_b)\)区间的概率就应该是 \[ P = \int_{x_a}^{x_b}f(x)\mathrm{d}x = F(x_b) - F(x_a) \] 于是我们就得到了一种采样方法，即在均匀分布中随机抽样一个数\(y\)，然后把这个\(y\)的数值映射到\(x\)上，即\(x = F^{-1}(y)\)，这样选出来的\(x\)就满足\(f(x)\)的分布了.

在蒙特卡洛模拟中，确定粒子随机发射的角度是就是采用这种方法去进行抽样的. 从下图可以看到，一个点向外辐射，不同方位处的辐射强度是不一样的，越往上或者越往下的投影面积会更小，所以对应的发射强度会小一些. 这个投影面积的大小，就是立体角，也就是我们确定粒子发射位置的概率分布，哪里面积越大哪里的发射概率就越大， \[ \mathrm{d}\Omega = \sin\theta\mathrm{d}\theta\mathrm{d}\phi \]

\(\phi\)方向完全是均匀的，只需要在\(\phi \in (0, 2\pi)\)做一个均匀采样就可以了，对于\(\theta\)方向，我们可以对它作归一化， \[ f(\theta) = \frac{\sin\theta}{2}, \theta \in (0, \pi) \] 它的累积分布函数为， \[ F(\theta^*) = \int_0^{\theta^*}f(\theta)\mathrm{d}\theta = \int_0^{\theta^*}\frac{\sin\theta}{2}\mathrm{d}\theta = \frac{ 1 - \cos\theta^*}{2} \]

\[ \therefore \theta^* = \arccos(1- 2F(\theta^*)) \]

所以我们对仰角的抽样方式就是在\((0,1)\)间均匀采样一个\(R_\theta\)，然后去计算\(R_\theta\)对应的角度， \[ \theta = \arccos(1 - 2R_\theta) \] 当然在实际模拟中我们不需要求反三角函数，只需要计算\(\cos\theta\)就可以确定粒子的发射方向了.

在粒子模拟的蒙特卡洛中，基本都是用这种直接法去进行抽样的，只不过角度抽样存在解析的表达式，其他性质的抽样不存在解析的表达式，只能采用查找表的方式进行数值抽样. 比如想要在声子色散中按照\(f(\omega)\)的分布抽样声子频率，我们可以把整个色散曲线切成好多段，每一段的概率分布就是\(f(\omega)\Delta\omega\)，第\(i\)段的累积分布函数就是 \[ F_i(\omega) = \frac{\sum_{j=0}^i f(\omega_j)\Delta \omega}{\sum_{j=0}^N f(\omega_j)\Delta \omega} \in (0, 1) \] 在构造好了离散化的累积分布函数后，可以在\((0,1)\)间进行均匀采样，然后用一些查找算法，比如二分查找（numpy中的searchsorted函数就是二分查找算法）去确定这一段的频率，相当于数值求解\(F^{-1}\).

接受拒绝采样

接受拒绝采样的基本方式是，在\((a, b)\)中均匀采样一个数\(x\)，再从\((0,1)\)中均匀采样一个数\(r\)，如果\(r <= f(x)\)，那么这次采样就被接受了. 如果\(r > f(x)\)，这次采样就被拒绝. 重复足够多的次数，就可以抽样出来\(f(x)\)的分布了. 这类似于用蒙特卡洛法求圆的面积. 这种采样方式的缺点是当\(f(x)\)的分布非常尖锐时，大量的点都被舍弃了，导致计算效率很低. 这种方法.. 不知道在蒙特卡洛中有没有应用.

复合采样

我们可以用直接法去按照有解析表达式的辅助分布函数\(g(x)\)采样一个数\(x\)，再从\((0,1)\)中均匀采样一个数\(r\)，如果\(g(x)r <= f(x)\)，那么这次采样就被接受了，反之这次采样就被拒绝了. 实际上就相当于之前撒点的范围为\((0,1)\)，现在撒点的范围变成\((0, g(x))\)了，需要把这个均匀采样压缩一下. 这种方式减少了\(f(x)\)和\(g(x)\)之间的差异，也就减少了被拒绝的次数，从而提高了采样效率.