蒙特卡洛中的频率抽样
声子蒙特卡洛模拟中的频率抽样
这里有一个20年邵成博士报告、超哥和郝磬老师做嘉宾的声子蒙特卡洛模拟的讲座
蒙特卡洛(MC)模拟实际上核心只包含两个过程,Drift+Scatter,模拟的粒子在体系内沿直线运动(Drift),在运动过程中会有一定几率受到散射(Scatter),散射后继续自由运动. 散射分为弹性散射和非弹性散射,在发生弹性散射时,动量和能量保持守恒,发生散射后粒子的性质保持不变,只有它的运动方向需要重新抽样. 声子-杂质散射或者在电子MC模拟中的电子-声学声子散射都属于弹性散射.
在发生非弹性散射时,粒子的性质会发生改变. 以声子蒙特卡洛为例,声子-声子散射会重置当前声子的状态. 我们认为声子-声子散射过程是没有记忆的,也就是说发生散射前这个声子的状态对它散射后的状态没有任何影响,它的新状态总是需要在整个允许空间里重新抽样. 在声子蒙特卡洛模拟中,一般都会采用各向同性假设,这个假设意味着被模拟粒子的性质和运动方向无关,只与频率(不同声子支是不同的,模拟三支声子,可以理解为三个抽样数组)有关,即散射后粒子的状态重新抽样过程,可以解耦为频率抽样和方向抽样,且方向抽样均为在蒙特卡洛中的采样里介绍的各向同性兰贝特发射. 在电子蒙特卡洛模拟中,由于有些散射机制的散射率是与方向有关的,所以散射后的方向抽样公式会和兰贝特发射存在一些差别. 在灰体近似下,我们认为声子的性质与频率无关,也就是说灰体蒙特卡洛模拟中,只存在方向抽样这个过程.
散射时间的确定
那么如何确定粒子Drift多久后会发生散射呢?我们可以假设现在共有\(N\)个粒子在漂移,\(\Gamma\)是粒子的散射率(也就是弛豫时间的倒数),被散射掉的声子数目显然和现有的声子数成正比,经过\(\mathrm{d}t\)时间后,存在 \[ \begin{gather*} \mathrm{d}N = -N\Gamma\mathrm{d}t \\ \therefore \frac{\mathrm{d}N}{N} = -\Gamma \mathrm{d}t \\ \therefore \frac{N_0 - N}{N_0} = 1 - \exp(-\Gamma t) \end{gather*} \] 可以看到对数关系实际上描述了函数增长率和函数值成正比的这种情况,经过了\(t\)时间被散射的声子占总声子数的比例是\(1 - \exp(-\Gamma t)\),当我们只考虑一个粒子的时候,就等价于这个粒子经过了\(t\)时间被散射的概率为\(p(t) = 1 - \exp(-\Gamma t)\). 这个\(P(t)\)已经相当于是累积分布函数了, 所以我们可以像在蒙特卡洛中的采样里介绍的一样,抽样一个\(R_t \in (0,1)\)的随机数,此时有 \[ \begin{gather*} R_t = 1 - \exp(-\Gamma t) \\ \therefore t = - \frac{1}{\Gamma}\ln (1 - R_t) \end{gather*} \] 不同频率声子的\(\Gamma\)不同,所以他们的散射时间也不相同. 在方程左右可以同时乘一个群速度\(v_g\)再除以一下体系的特征尺寸\(L\),就得到了超哥文章里的基于努森数的表达式, \[ \bar{l} = - Kn \ln(1 - R_t) \] > 华钰超, 董源, 曹炳阳. 硅纳米薄膜中声子弹道扩散导热的蒙特卡罗模拟. 物理学报, 2013, 62(24): 244401
从这个表达式也可以看出来,在灰体声子蒙特卡洛模拟中,我们什么声子性质都不需要,只需要给定系统的努森数就好了,那些声子性质都是用来对结果做后处理的.
散射后频率的确定
处理散射过程的关键,就是如何抽样散射后粒子的性质,对于声子来说也就是声子频率(某个声子支的某个频率). 本质上各种模拟各种抽样的概率计算方式都是一样的,就是抽样概率和它占有的份数成正比,比如对于角度发射,就是发射概率和立体角大小成正比. 假如有\(\omega_1, \omega_2, \omega_3\)三种频率,这三种频率的个数分别为\(n_1, n_2, n_3\),那么抽中\(\omega_2\)的比例就是 \[ P(\omega_2) = \frac{n_2}{n_1 + n_2 + n_3} \] 实际操作就像蒙特卡洛中的采样中介绍的在均匀分布中抽随机数就好了. 不同的模拟方法中的模拟对象可能不同,所以导致了份数的统计方式不同,最终导致了抽样概率公式的表达式不同. 在声子蒙特卡洛模拟中,一般存在两种模拟方式,一种是对声子团进行模拟,此时\(n_1, n_2, n_3\)代表不同频率的声子数目;另一种是对声子能量团进行模拟,此时\(n_1, n_2, n_3\)就代表不同频率的声子能量,因此这导致了不同的模拟方式中抽样概率表达式的区别. 另一方面,从边界发射的声子相当于从热流分布中抽样,内部发射的声子相当于从能量分布中抽样,这也导致了边界发射抽样概率和内部散射抽样概率表达式的区别.
前一种蒙特卡洛模拟的代表性文章是
Hao Q, Chen G, Jeng M S. Frequency-dependent Monte Carlo simulations of phonon transport in two-dimensional porous silicon with aligned pores[J]. Journal of Applied Physics, 2009, 106(11): 114321.
后一种蒙特卡洛模拟的代表性文章是
Péraud, Jean-Philippe M., and Nicolas G. Hadjiconstantinou. "Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations." Physical Review B 84.20 (2011): 205331.
前两种都是Ensemble系综声子蒙特卡洛,在Dr. Hua和Quasi Dr. Li的Tracing声子蒙特卡洛模拟中,模拟的对象也不是声子,而是声子能量团,所以抽样的方式和后一种蒙特卡洛是一样的,只不过此时我们假设系统内的温差并不大,即散射率和温度无关,此时抽样概率表达式可以进一步简化,简化的推论就是我们不再需要同时模拟很多个声子来获得实时统计模拟过程中不同位置的温度分布,而是可以单独追踪每一个声子,从而大幅提高了模拟效率. 在电子蒙特卡洛中,也有着类似的处理方式,我们将它称之为Single Particle Monte Carlo. 只不过电子的复杂性在于它是受到电场力的,而声子是不受力的. 所以即使一次只模拟一个电子,我们还是需要不断求解泊松方程更新电压场,不断进行蒙特卡洛更新电流场,迭代多次直到收敛。
Li, Han-Ling, Junichiro Shiomi, and Bing-Yang Cao. "Ballistic-diffusive heat conduction in thin films by phonon monte carlo method: Gray medium approximation versus phonon dispersion." Journal of Heat Transfer 142.11 (2020).
粒子数MC和能量偏差MC
我们知道温度在非平衡状态下是基于局域能量平衡定义的,所以我们基于求解玻尔兹曼方程来得到系统的温度分布,本质上得到的是系统的能量分布,在以声子为载热子的半导体中,也就是声子或声子能量的分布. 声子蒙特卡洛模拟的基本思想就是撒大量的点(声子),去近似这个分布. 从这个角度来讲,声子蒙特卡洛模拟和用投针法去估计圆的面积也没有什么本质的区别. 其他的蒙特卡洛模拟,比如分子蒙特卡洛就是近似体系在某个系综中的分布,量子蒙特卡洛估计就是近似体系波函数了.. 下面这张图示意着局域声子能量沿着频率的分布,即不同频率声子能量的占比. 在基于粒子的蒙特卡洛里,可以理解为生成很多很多个小方块,去近似这个分布,类似于数值积分中做的一样.

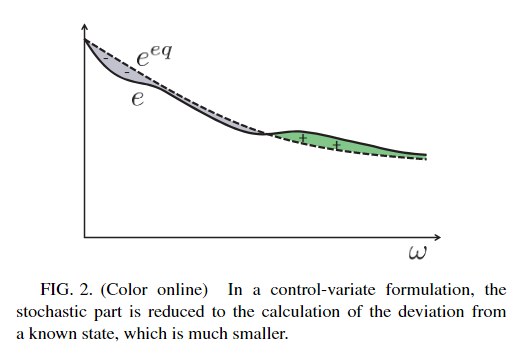
可以看到这种这种粒子蒙特卡洛需要近似整个分布,即我们需要逼近的面积是整个函数围成的面积,导致需要很多的声子才能降低统计误差. 而当系统内存在的温差比较小时,我们可以选定一个参考温度\(T_{eq}\),此时系统内部的能量分布也非常接近于根据参考温度计算的平衡分布\(f_{T_{eq}}(\omega) = \frac{1}{\exp(\frac{\hbar\omega}{k_bT} - 1)}\). 所以能量偏差(Energy-based variance reduced)蒙特卡洛的基本想法就是撒出的声子只去近似偏离参考分布的部分(下图中标注了颜色的部分),而不是去近似整个分布,相当于逼近的面积大幅减少了. 这种处理大幅降低了模拟的统计偏差,同时提高了模拟效率. 这两种方法的区别,就像蒙特卡洛中的采样中介绍的原始版的接受拒绝采样和复合采样之间的区别.
初始化抽样
在基于粒子的蒙特卡洛中,我们初始化系统中的声子是根据平衡态的玻色爱因斯坦分布生成的,我们给定体系的初始温度分布,画好网格,假设某个网格的温度为\(T\),网格大小为\(V\),那么这个网格中的声子总数就为, \[ N = V\sum_p \int_{\omega=0}^{\omega_m} D(\omega, p) f^{eq}_{T}(\omega)\mathrm{d}\omega \] \(D(\omega, p)\)是态密度,即频率为\(\omega\)的声子态共存在多少个,\(f_T^{eq}(\omega)\)是温度为\(T\)时,频率为\(\omega\)的某个声子态上共存在多少个声子,所以这两个乘起来再对所有的频率和声子支求和,就是得到系统内总的声子数目. 我们假设模拟的一个声子团代表\(N_{\text{eff}}\)个声子,那么我们在一个小格子里就要生成\(N/N_{\text{eff}}\)个声子团. 每个声子团都具有不同的频率,初识化时声子团的频率按照\(D(\omega, p)f^{eq}_T(\omega)\)的权重去抽样,因为\(D(\omega, p)f^{eq}_T\)就代表着这个频率的声子数目.我们统计局域格点能量时,也是去统计格点里所有声子团的能量之和, \[ E = N_{\text{eff}}\sum_i \hbar\omega_i = V\sum_p\int_{\omega=0}^{\omega_{m}} \frac{D(\omega, p)\hbar\omega}{\exp(\frac{\hbar\omega}{k_b T}) - 1} \mathrm{d}\omega \] 等式右侧的\(T\),就是局域平衡温度,在系综声子蒙特卡洛中温度就是通过上面这个式子来计算的。这个过程实际上相当于在确定性方法中求解能量守恒方程,
Li R, Lee E, Luo T. Physics-informed neural networks for solving multiscale mode-resolved phonon Boltzmann transport equation[J]. Materials Today Physics, 2021, 19: 100429.
玻尔兹曼方程为 \[ \frac{\partial f_\omega}{\partial t} + |v_g| \vec{s}\cdot \nabla f_\omega = - \frac{f_\omega - f_\omega^0(T)}{\tau_\omega} \] 在玻尔兹曼方程左右两侧同时乘上\(\hbar\omega D(\omega)\)后,再对立体角和频率积分,就得到了能量守恒方程,能量守恒要求积分值为0,于是, \[ \frac{\partial e}{\partial t} + \nabla \cdot \vec{q} = - \sum_p \int_{\omega=0}^{\omega_m}\int_{\Omega} \hbar\omega D(\omega) \frac{f - f_0}{\tau(\omega)} \mathrm{d}\Omega \mathrm{d}\omega = 0 \] 所以BTE描述了这样一个事实,每个空间位置都有一个局域平衡温度,我们可以用这个温度来计算该位置各频率声子的平衡玻色爱因斯坦分布, \[ f^0_\omega (T) = \frac{1}{\exp(\frac{\hbar\omega}{k_bT}) - 1} \] 该位置各个频率、各个方向的分布函数\(f\)都偏离并围绕在该频率对应的平衡分布的附近,BTE等式右侧的碰撞项就是分布\(f_\omega\)与该频率平衡分布之差再除以该频率的弛豫时间,所以能量守恒方程也就相当于是计算局域平衡温度的方程,建立了\(f_\omega\)和\(f_\omega^0(T)\)之间的关系. 在BTE的求解过程中,\(f_\omega^0(T)\)和\(f_\omega\)都是不知道的,所以玻尔兹曼方程加上能量守恒方程,这个方程组才封闭,离散坐标法解的也就是这两个方程.
李含灵, 曹炳阳. 微纳尺度体点导热的拓扑优化. 物理学报, 2019, 68(20): 200201
在能量偏差的蒙特卡洛里,我们模拟的东西并不是声子团,而是声子能量团,每个声子能量团代表的能量都是一样的,所以当他们的频率不一样时,实际上代表了这一团里包含的声子数目不同. 假如初始化时当前格子里的温度为\(T\)高于参考温度\(T_{eq}\),那么当前格子相对参考温度的能量偏差就是 \[ \begin{aligned} \Delta E &= \sum_p \int_{\omega=0}^{\omega_m} \hbar\omega D(\omega, p) \times \left[ f_T(\omega) - f_{T_{eq}}(\omega)\right] \\ &= \sum_p \int_{\omega=0}^{\omega_m} \hbar\omega D(\omega, p) \times \left[\frac{1}{\exp(\frac{\hbar\omega}{k_bT})- 1} - \frac{1}{\exp(\frac{\hbar\omega}{k_bT_{eq}}) - 1} \right] \end{aligned} \] 假设一个模拟的声子能量团代表\(\xi_{\text{eff}}^d\)的能量,那么我们在这个小格子里就要生成\(\Delta E / \xi_{\text{eff}}^d\)个声子能量团. 每个声子能量团都具有不同的频率,我们这个时候就不能够按照\(D(\omega, p)f_T^{eq}(\omega)\)这个权重去抽样了, 因为它代表着这个频率的总声子数目,我们现在模拟的对象是声子能量偏差,需要按照某个频率的总能量偏差去抽样,即按照 \[ D(\omega, p)e^d(\omega) = \hbar\omega D(\omega, p) \left[ \frac{1}{\exp(\frac{\hbar\omega}{k_bT}) - 1} - \frac{1}{\exp (\frac{\hbar\omega}{k_b T_{eq}}) - 1}\right] \] 这个权重去抽样. 当然实际数值模拟中不可能总去算指数,一般都是先算好一张对应表,然后用二分查找去确定对应温度或频率的数值.
散射抽样
散射后频率的确定和初始化过程中频率抽样的区别就是需要把原始的权重函数除以一个频率相关的弛豫时间,频率越高的声子,其被散射的概率就越大. 此外,此时权重中的平衡分布中的温度\(T_{\text{loc}}\),也要采用基于除以弛豫时间的假能量(pseudoenergy)来定义,
\[ \begin{aligned} \tilde{E} &=N_{\mathrm{eff}} \sum_{i} \frac{\hbar \omega_{i}}{\tau\left(\omega_{i}, p_{i}, T\right)} \\ &=V \int_{\omega=0}^{\omega_{\max }} \sum_{p} \frac{D(\omega, p) \hbar \omega}{\tau(\omega, p, T)} \frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{\mathrm{loc}}}\right)-1} d \omega, \end{aligned} \] 所以在基于粒子的蒙特卡洛中,散射后的频率确定权重为 \[ \frac{D(\omega, p )f^{\text{loc}}}{\tau(\omega, p, T)}. \] 在能量偏差的蒙特卡洛中,这个权重就要相应地从粒子数替换成能量偏差, \[ \begin{aligned} &\frac{D(\omega, p)\left(e^{\text {loc }}-e_{T_{e q}}^{e q}\right)}{\tau\left(\omega, p, T\right)} \\ &=\frac{D(\omega, p) \hbar \omega}{\tau\left(\omega, p, T\right)}\left(\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b}\left[T_{\text {loc }}\right]_{j}}\right)-1}-\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{e q}}\right)-1}\right) \end{aligned} \] 在一个格子里面散射,散射后格子内的总能量应该是守恒的,而在基于粒子的蒙特卡洛中不同频率声子团的能量是不一样的,所以散射完之后格子内的能量可能不再守恒,这时候需要按照当前格子散射前温度的平衡分布随机增加或者删除声子,直到格子内的能量恢复到发生散射前的能量. 而在能量偏差的蒙特卡洛中,每一份声子能量团的能量都是相等的,只不过有的声子能量团能量为正,有的声子能量团能量为负,因为他们代表能量偏差. 假如在格子里抽样时选中了\(N_{s,j}^+\)个正能量的声子能量团,\(N_{s,j}^{-}\)负能量的声子能量团,那么最后我们只会选中\(|N_{s,j}^{+} - N_{s, j}^{-}|\)个能量团让他们发生散射,并且把他们的符号都设置为\(e^{\text{loc}} - e^{eq}_{T_{eq}}\)的符号,并删除掉其余选中的能量团. 这样处理会保证格子内的能量在散射前后是守恒的,不再需要额外发射或者删除声子。
边界发射抽样
边界发射和内部散射的区别就是,后者是在局域能量中抽样,而前者是在边界热流中抽样. 所以后者的抽样权重是各频率对能量的贡献,前者的抽样权重是各频率对边界热流的贡献. 对于恒温热沉边界,它的分布是满足平衡玻色爱因斯坦分布的,因此分布函数是各向同性的,对立体角的积分不涉及分布函数。此时热流强度的表达式为, \[ Q = q\Delta t = \Delta t\sum_p \int_{\Omega \, \text{in}\, 2\pi} \int_{\omega=0}^{\omega_m} \hbar\omega D(\omega)f^{eq}(T_b)v_g \vec{s}\cdot\vec{n} \mathrm{d}\omega\mathrm{d}\Omega \] 其中\(\vec{n}\)为边界的法向量,\(\vec{s}\)为声子发射的方向向量. 当内部点热源发射时,我们只需要考虑立体角的分布就可以了. 而当边界面热源发射时,除了立体角,我们还需要考虑可见面积的影响,越垂直于发射面的地方热流强度越大,所以我们还需要乘一个相对于发射平面法向量的\(\cos\theta\).


我们可以把坐标轴挪到发射边界上,此时热流强度的表达式就可以改写为, \[ \begin{aligned} Q &= \Delta t\sum_p \int_0^{2\pi} \int_0^{\pi/2} \int_{\omega=0}^{\omega_m} \hbar\omega D(\omega)f^{eq}(T_b)v_{g, \omega} \mathrm{d}\omega\cos\theta\sin\theta \mathrm{d}\theta\mathrm{d}\phi \\ &= \Delta t \sum_p \int_{\omega = 0}^{\omega_m}\frac{1}{4} \hbar\omega D(\omega) f^{eq}(T_b) v_{g, \omega} \mathrm{d}\omega \end{aligned} \] 所以对于等温边界,基于粒子数的蒙特卡洛的发射抽样权重就是 \[ D(\omega)f^{eq}(T_b)v_{g, \omega} \] 和散射过程抽样的差别就是少除了一个弛豫时间多乘了一个群速度.
对于能量偏差的MC来说,这个热流就相应变为了和参考温度热流的偏差, \[ \begin{aligned} q_{\omega, b}^{\prime \prime}=& \frac{1}{4} \sum_{p} D(\omega, p) v_{g, \omega} \hbar \omega \\ & \times\left(\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{b}}\right)-1}-\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{e q}}\right)-1}\right) \end{aligned} \] 此时的抽样权重为 \[ D(\omega)v_{g, \omega} \hbar\omega\left(\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{b}}\right)-1}-\frac{1}{\exp \left(\frac{\hbar \omega}{k_{b} T_{e q}}\right)-1}\right) \]
Tracing Monte Carlo
我们查看一下能量偏差能量卡洛中散射抽样概率的表达式: \[ \begin{aligned} \frac{D(\omega, p) \hbar \omega}{\tau\left(\omega, p, T\right)}\left(f_{\omega}(T_{\text{loc}}) - f_{\omega}(T_{eq})\right) \end{aligned} \] 假设体系温差相对于参考温度偏差不大,我们可以对这两个分布函数之差做差分近似, \[ f(T_{\text{loc}}) - f(T_{eq}) \approx (T_{\text{loc}} - T_{eq}) \frac{\mathrm{d}f_{\omega}}{\mathrm{d}T} \Big|_{T=T_{eq}} \] 同时把弛豫时间中的温度直接设置为参考温度,我们可以得到新的抽样概率表达式为, \[ \begin{aligned} \frac{D(\omega, p) \hbar \omega}{\tau\left(\omega, p, T_{eq}\right)}(T_{\text{loc}} - T_{eq}) \frac{\mathrm{d}f_{\omega}}{\mathrm{d}T} \Big|_{T=T_{eq}} \end{aligned} \] 而在同一个网格内抽样,\(T_{\text{loc}} - T_{eq}\)这一项大家都是相等的,对权重没有影响,我们又知道 \[ C_\omega = \hbar\omega D(\omega)\frac{\mathrm{d}f_\omega}{\mathrm{d}T} \] 可以参考之前写过的从声子色散到热导率. 此时抽样概率表达式就变成了 \[ \frac{C(\omega, p)}{\tau(\omega, \rho, T_{eq})} \] 同理,边界热流的抽样概率表达式就变成了 \[ C(\omega, p)v_{g,\omega, p} \] 就得到了含灵师兄或者Péraud文章里抽样概率的表达式
Péraud J P M, Hadjiconstantinou N G. An alternative approach to efficient simulation of micro/nanoscale phonon transport[J]. Applied Physics Letters, 2012, 101(15): 153114.
Li, Han-Ling, Junichiro Shiomi, and Bing-Yang Cao. "Ballistic-diffusive heat conduction in thin films by phonon monte carlo method: Gray medium approximation versus phonon dispersion." Journal of Heat Transfer 142.11 (2020).
所以Tracing方法正常情况下是没法考虑温度对散射率的影响的,而在小温差下Tracing应该和Ensemble给出一样的结果,当温差较大时可能存在一定的区别,在电子器件里能影响多少呢..