Electron Monte Carlo (1) - 散射

电热输运

Electron Monte Carlo (1) - 散射

晶体管为什么产热

电子大体上存在两类散射，弹性散射和非弹性散射，弹性散射只影响电子的动量，而不影响电子的能量，非弹性散射既影响电子的动量也影响电子的能量。导带中的自由电子从电场获得能量加速，在运动的过程中通过和晶格碰撞将能量传递给声子，热量于是产生了。电场给了电子加速的作用，散射则限制了电子的速度，电子的输运实际上就是这两个作用的平衡。当晶体管的尺寸很小，比如和电子的自由程相当（5 - 10 nm），电子没发生足够的非弹性散射就跑掉了，能量并没有完全传递给声子，这两个能量系统间就处于不平衡的状态，此时焦耳定律会高估产热，因为一部分能量通过热电子直接从接触耗散了.

能量小于50 meV的电子主要和声学声子发生散射，更高能量的电子主要和光学声子发生散射，光学声子再退化到声学声子。光学声子退化到声学声子的速度是很慢的，所以可能会发生什么呢？高能电子大量发射光学声子，但是光学声子来不及退化到声学声子，导致局域的光学声子发生累积，使得局域散射率增加，电子的运动被阻碍，将这个现象称为phonon energy bottleneck。从这个过程也可以看出不同能量系统间的相互影响机制，就是散射，在Monte Carlo模拟中只要通过系统间传递的信息来修改散射率就可以体现这一过程了。所以所谓的cross-scale的模拟，并不是像A x B x C这种大家都搅在一起混乱的过程，而是类似A -> B -> C -> A -> B -> C -> converge，每一个系统本身还是独立的。

另一方面，在高场区域下声子散射具有非局域的特点，电子在电场尖峰下获得大部分的能量，但是在将能量完全传递给晶格之前，往往需要漂移几个平均自由程的路径，因此实际产热尖峰位置相比于基于漂移-扩散模型算出来的焦耳热，大概会偏移几个电子自由程的距离，尖峰的高度会扁一些。

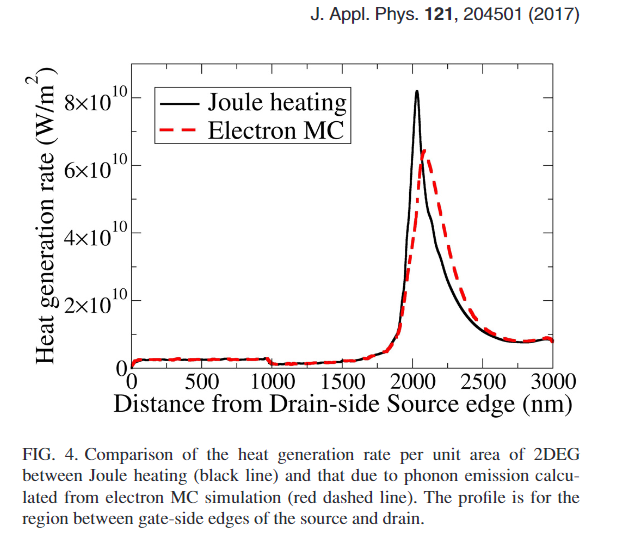
image-20221111101217943

各种载流子的Monte Carlo模拟可以很好地帮助理解波粒二象性.. 倒空间中波的性质，色散关系（频率+群速度）和弛豫时间，决定了载流子的可能状态；而载流子本身在正空间中运动，受到外界条件和边界条件的制约。电子运动和声子运动的区别在哪里呢？一个主要的区别就是电子会受到电场力的驱动，在Monte Carlo模拟的同时要求解泊松方程和连续性方程，而声子是不受力的。这个区别使得在Monte Carlo模拟中，对电子散射要额外做一些处理。

自散射

假设\(\Gamma\)为散射率，那么载流子在两次散射事件间的自由飞行时间就可以抽样为 \[ 1 - r = \exp\left[-\int_0^{t_r}\Gamma\left[\mathbf{k}(t^\prime)\right]\mathrm{d}t^\prime\right] \] 其中\(r\)是\((0,1)\)的随机数，\(\mathbf{k}\)是载流子波矢，在抽样确定了\(r\)之后，就可以通过这个等式关系把两次散射间的自由飞行时间\(t_r\)确定下来。

对于声子来说，由于两次散射间声子不受外力，因此自由飞行期间\(\mathbf{k}\)是始终保持不变的，于是这个等式可以简化成 \[ 1 - r = \exp\left[-\Gamma(\mathbf{k_0})t_r\right] \] 于是 \[ t_r = - \frac{1}{\Gamma(\mathbf{k_0})} \ln(1-r) \] 对于电子来说，由于它始终受到电场力的作用，波矢一直在发生变化，\(\Gamma\left[\mathbf{k}(t^\prime)\right]\)也相应在一直发生变化，这使得自由飞行时间无法整理成声子这样简单的形式。于是semiconductor people引入了self-scattering方法，它引入了一项虚拟的散射机制\(\Gamma_\text{self}\)，这个散射机制的散射率自动调整以使得总散射率（自散射率+真实散射率）保持不变， \[ \Gamma_t = \Gamma(t^\prime) + \Gamma_\text{self}(t^\prime) \] 此时，我们就可以像声子一样来确定自由飞行时间了， \[ t_r = - \frac{1}{\Gamma_t}\ln(1-r) \] 这个\(\Gamma_t\)只是用来确定电子是否发生散射，在发生散射后，我们再根据各个散射机制散射率的大小确定发生了哪种散射， \[ \Gamma_t = \Gamma_\text{self}(\mathbf{k}) + \Gamma_1(\mathbf{k}) + \Gamma_2(\mathbf{k}) + \ldots + \Gamma_N(\mathbf{k}) \] 其中\(\mathbf{k}\)是自由飞行结束后（在\(t_r\)时间内经电场加速后）电子的波矢，如果抽中了自散射，电子的所有性质保持不变，进入下一个自由飞行。所以\(\Gamma_t\)的选取要确保在整个模拟时间内大于电子可能的最大真实散射率。

散射机制

声子的散射机制是比较简单的，在常温以上，基本就两种散射，本征散射（or Umklapp散射 or 三声子散射）和杂质散射。本征散射重新抽样声子状态，而杂质散射只改变声子的运动方向，不改变声子的能量。而由于本征散射一般远大于杂质散射，因此仿真中全部重新抽样影响也不大。

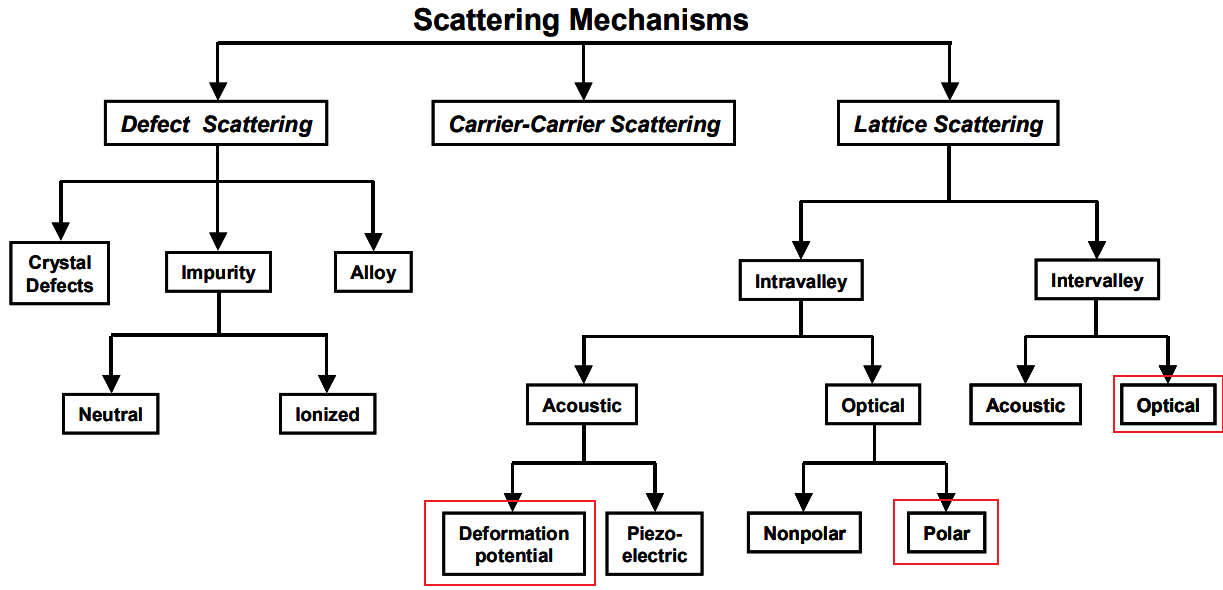
image-20221110202207773

电子的散射机制就要复杂许多，虽然大体分类可以分为弹性散射和非弹性散射，但具体机制如上图所示的一样，不同材料中起主要作用的散射机制会有些区别，其中最重要的，就是Lattice Scattering，电子和晶格之间发生的相互作用，也就是电子和声子的相互作用，这也是半导体发热的根源。在计算散射率的时候，采用基于微扰论的费米黄金定则（所以我们称电子Monte Carlo是半经典的，用量子的性质驱动经典的运动）， \[ \Gamma(\mathbf{k})=\frac{2 \pi}{\hbar} \sum_{\mathbf{k}^{\prime}}\left|M_{\mathbf{k k}^{\prime}}\right|^2 \delta\left(E_{\mathbf{k}}-E_{\mathbf{k}^{\prime}} \pm \Delta E\right) \] 其中\(M_{\mathbf{k k}^{\prime}} = \langle \mathbf{k^{\prime}}|H^\prime|\mathbf{k}\rangle\)，\(H^\prime\)是该散射机制对应的势能，这个表达式是个典型的算符形式的内积.. 对于上式来说，弹性散射前后电子能量不发生变化\(\Delta E = 0\)，由于声学声子的能量比较小，因此在一般不需要太细致的情况下，声学声子散射可以认为是弹性的。而由于光学声子的频率很高，它无论如何都是非弹性的，\(\Delta E = \hbar\omega\)。从上面的图里可以看到，晶格散射可以分为两种，一种是Intravalley谷内散射，一种是Intervalley谷间散射。之前的文章里也提到过，

但幸运的是，电子满足的费米-狄拉克分布告诉我们，电子的数目在超过费米能级后，其数目会随着能量的增加而大幅衰减. 因此，对于电子导电的半导体来说，自由电子可能允许的状态基本都集中在导带的底部，相当于被困在了这个势阱里. 因此对于大部分情况来说，我们没有必要给出所有的导带形貌，我们只需要对导带底部做出一些合理的描述即可. 由于导带底部是导带的能量最低点，相当于稳定平衡位置，而在平衡位置附近由于势能的一阶导数（力）为0，所以任何势能分布都可以采用二阶简谐来近似，也就是抛物线，弹簧的胡克定律或者固体物理中推导的晶格相互作用，都是基于这种近似得到的.

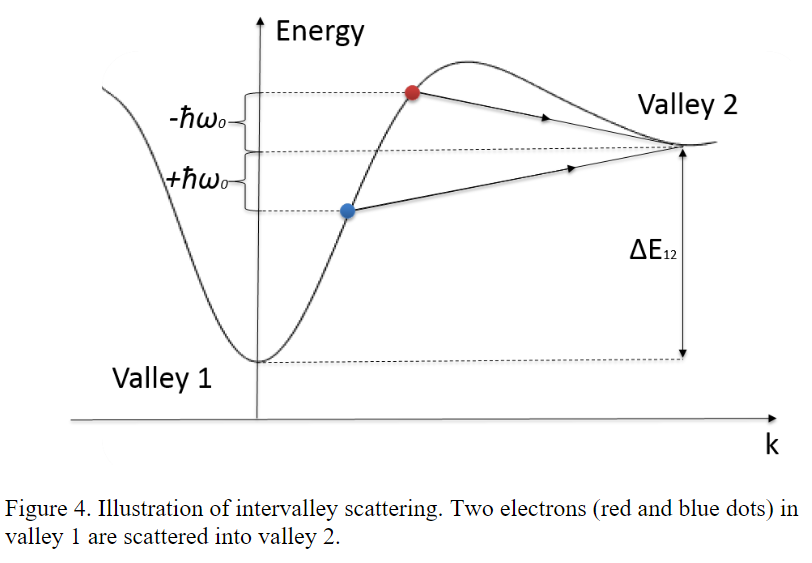
我们把一个能量面的各个局域最低点称作谷，当电子散射前后处于一个谷中时，我们就称这种散射为谷内散射；当电子散射后运动到另一个谷中时，我们称这种散射为谷间散射。对于谷内散射，对于硅这种极性很弱的材料来说，一般认为只有声学声子参与，而对于GaN这种极性很强的材料，极性光学声子散射是必须考虑的。

对于能量为\(E_k\)的电子，谷内弹性声学声子散射率的表达式可以写成， \[ \lambda_\text{ac}(E) = \frac{\pi k_bT}{\hbar} \frac{1}{\rho v_s^2} g(E_k)D_a^2 \] 其中\(v_s\)是声速，\(\rho\)是材料密度，\(D_a\)称为声学变形势能（acoustic deformation potential），\(g(E_k)\)是电子态密度，对于非抛物型能带，可以写成 \[ g(E_k) = \frac{(2m_d)^{3/2}}{2\pi\hbar^3}\sqrt{E_k\left(1 + \alpha E_k\right)}\left(1 + 2\alpha E_k\right) \] 对于谷间散射，电子的波矢变化很大，表达式可以整理成， \[ \lambda_{iv} = Z_{f} D_{iv}^2 \left(n_q(\omega_{op}) + \frac{1}{2}\mp \frac{1}{2}\right) g_f(E_K \pm \hbar\omega_{q}) \] 其中\(Z_f\)是散射后的等价能谷数目，\(n_q\)是玻色-爱因斯坦分布，\(g_f\)是散射后能谷的态密度，\(\omega_q\)是参与的散射的声子的频率。

image-20221110211615466

由于光学色散比较平缓群速度比较低，在声子输运过程的求解中，一般也只把光学声子系统当作一个纯热容系统，相当于在电子和声学声子的能量交换中起到一个中介的作用，在控制方程中没有输运的扩散项， \[ \frac{3 n k_B}{2} \cdot \frac{T_e-T_O}{\tau_{e-O}}=C_O \cdot \frac{T_O-T_A}{\tau_{O-A}} \] ## Silicon

硅有6个等价的椭球形valley，椭球的中心处于距离布里渊区原点的\(0.85\)倒格矢的位置处。在硅中，影响比较大的散射机制，主要是谷内声学声子散射和谷间声子散射。谷间散射可以分为两大类，一类是相邻的谷间发生散射，如下图的\(f\)过程，散射后等价能谷数目为4；另一类是对向的谷间发生散射，称为g过程，散射后等价能谷数目为1。

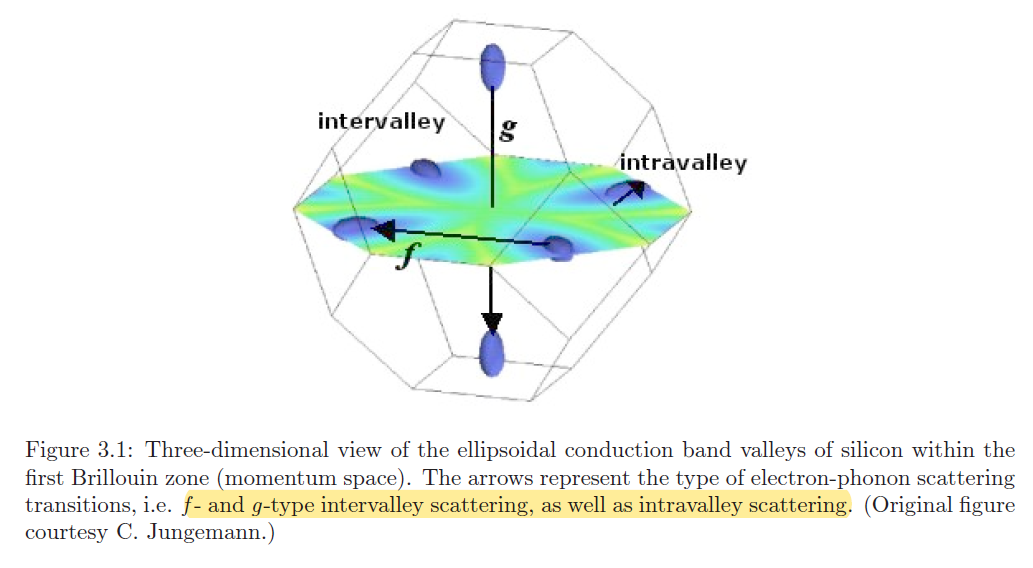
image-20221111105410225

在硅中，f散射和g散射都是U过程。在一般情况下，散射前后动量守恒，散射前后电子的波矢之差，等于参与的声子波矢之差；对于U过程，散射前后的电子波矢之差等于声子波矢之差再加上一个倒格矢G。

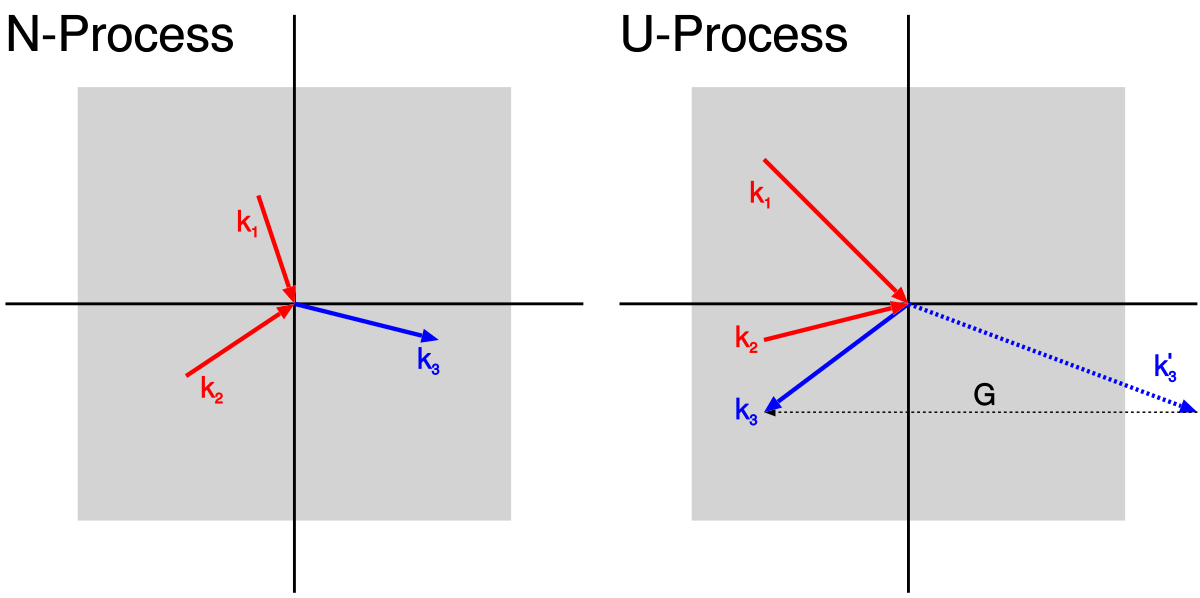
Umklapp scattering - Wikipedia

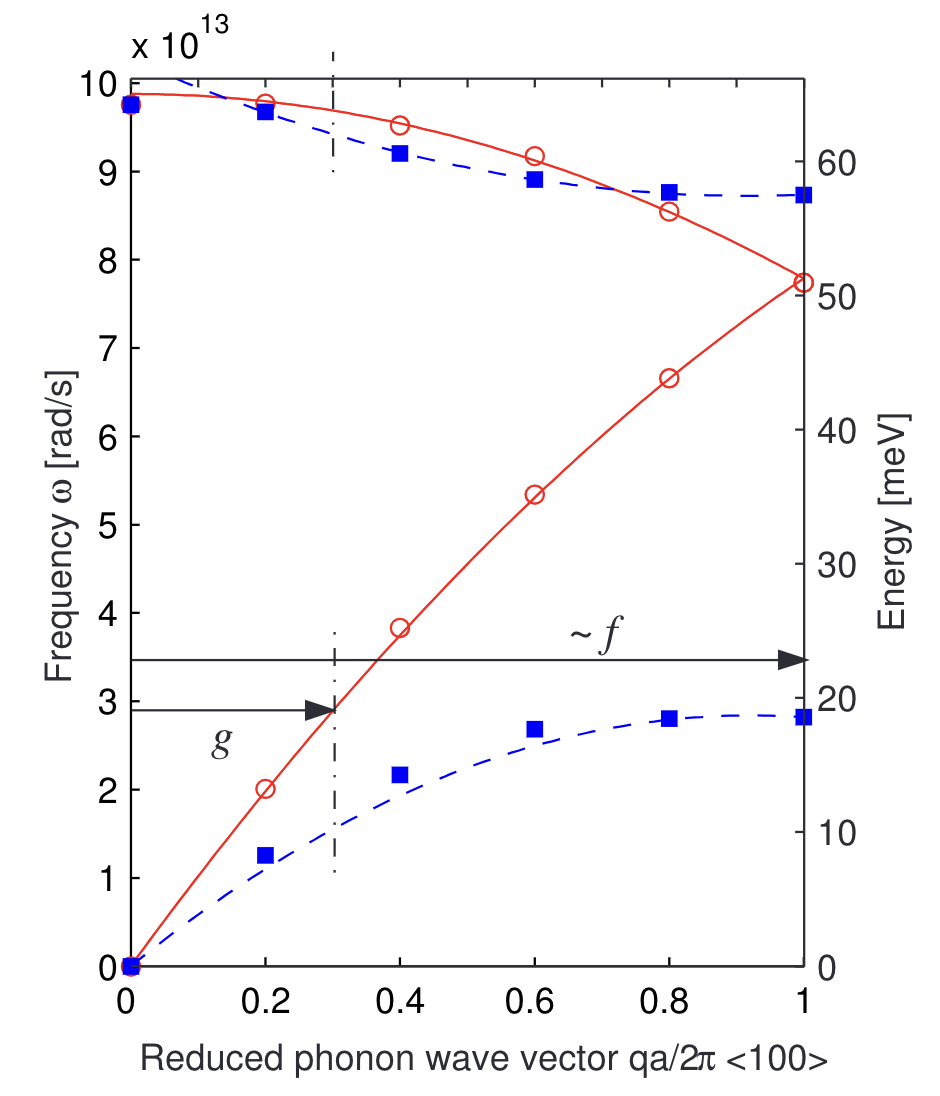
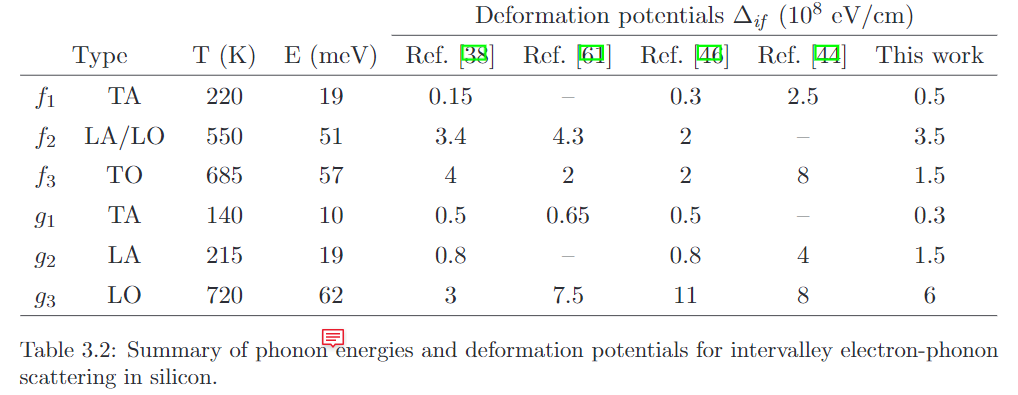
因此对于f散射来说，电子在两个能谷间跳跃导致的波矢变化是\((0, 0.85, 0.85)G\)，g散射能谷跳跃导致的波矢变化是\((1.7, 0, 0)G\)，减去一个倒格矢G，则对应的声子波矢则是\((1, 0.15, 0.15)G\)和\((0.3, 0, 0)G\)。下图是硅沿\(\langle 1 0 0 \rangle\)方向的声子色散，g声子的约化波矢就是0.3，f声子的约化波矢一般就认为处于布里渊区边界处。所以参与谷间散射的声子能量，分别在色散曲线上做两条竖线，与各声子支的交点，就是声子频率。f声子的LT和LO支频率重合，g声子的LO和TO的频率也几乎一样，所以硅的谷间散射最后可以认为一共存在\(8 - 2 = 6\)种类型，不同文献取的能量和对应散射的变形势能可能会有所区别。

Snipaste_2022-11-11_10-56-38

image-20221111122344085

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Silicon(object):
    def __init__(self):
        self.rho = 1.4516e+12
        self.hbar = 6.58211915e-16
        self.m0 = 5.68562975e-16
        self.kb = 8.61734318e-05
        self.ml = 0.91 * self.m0
        self.mt = 0.19 * self.m0
        self.md = (self.ml * self.mt * self.mt)**(1/3)
        self.alpha = 0.5
        self.T = 300
        self.vs = 9040e2
        
    def DOS(self, E):
        dos = (
                self.md ** (3 / 2) * np.sqrt(2)
                / (np.pi**2 * self.hbar**3)
                * np.sqrt(E * (1 + self.alpha * E))
                * (1 + 2 * self.alpha * E)
            )
        dos[np.isnan(dos)] = 0
        return dos
        
    def bose(self, E_phonon):
        return 1 / (np.exp(E_phonon / (self.kb * self.T)) - 1)
        
    def intervalley(self, E, D, E_phonon, Z_iv):
        scatOconst = np.pi / (2 * self.rho / self.hbar)
        Nq = self.bose(E_phonon)
        rate_em = Z_iv * D**2 * (Nq + 1) * self.DOS(E - E_phonon) * scatOconst / E_phonon
        rate_abs = Z_iv * D**2 * (Nq) * self.DOS(E + E_phonon) * scatOconst / E_phonon
        return rate_em, rate_abs
    
    def intravalley_a(self, E):
        D = 6.55
        return np.pi * self.kb * self.T / self.rho / self.hbar / self.vs**2 * D**2 * self.DOS(E)
    
######################################################################
si = Silicon()
E = np.linspace(0, 0.3, 301)
plt.plot(E, si.intravalley_a(E), label='intravalley acoustic', color='b', linestyle=':')
plt.plot(E, si.intervalley(E, 6e8, 62e-3, 1)[0], label='g3-em', color='r')
plt.plot(E, si.intervalley(E, 6e8, 62e-3, 1)[1], label='g3-ab', color='g')
plt.legend() 
plt.yscale('log')
plt.xticks([0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3])
plt.xlim(0, 0.3)
plt.ylim(1e10, 1e13)
plt.xlabel('Energy (eV)')
plt.ylabel(r'Scattering rate ($\text{s}^{-1}$)')

dodo

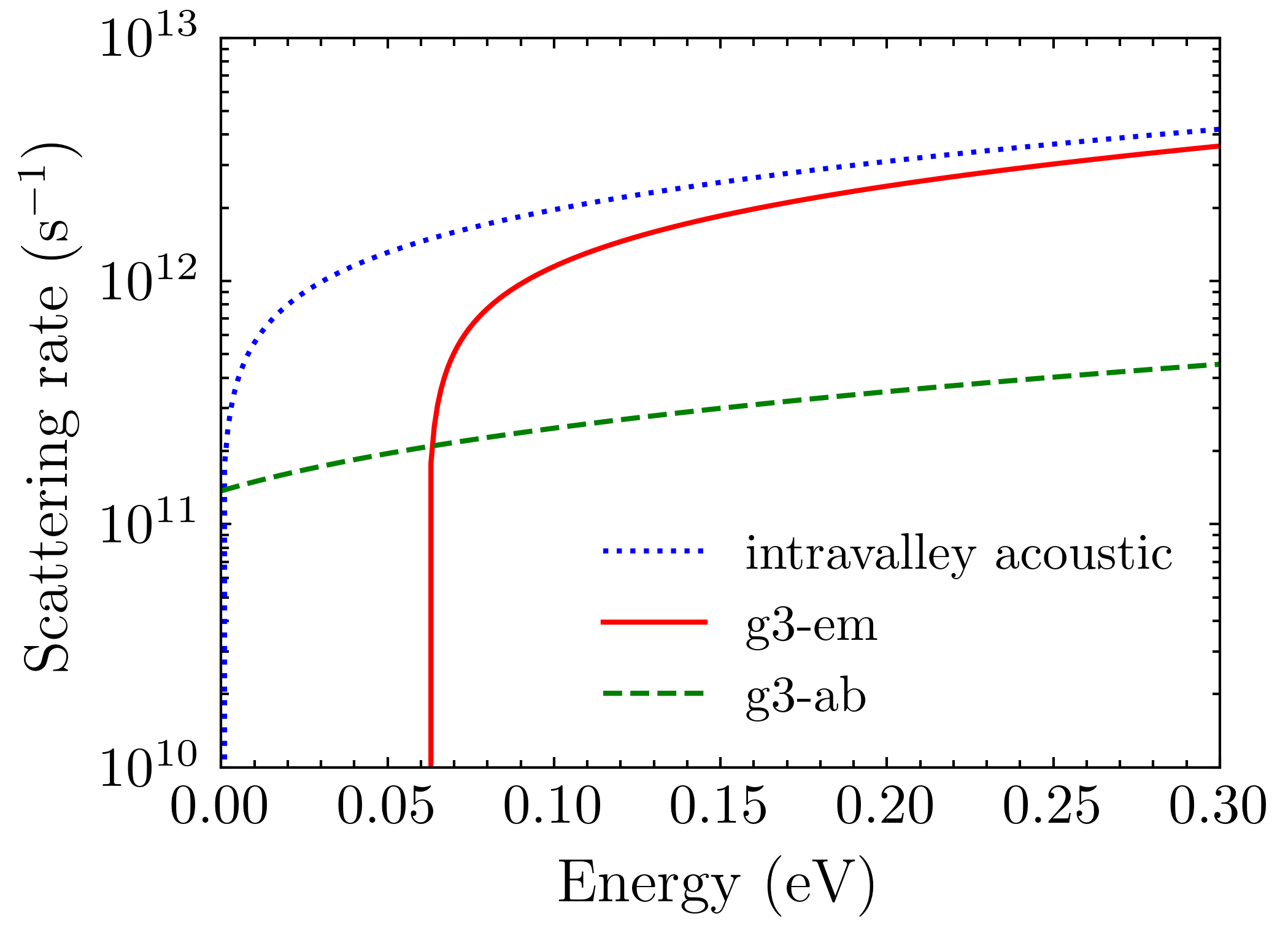
Reference

  1. Hao, Q., et al. "Multi-length scale thermal simulations of GaN-on-SiC high electron mobility transistors." Multiscale Thermal Transport in Energy Systems. Nova Science Publishers, 2016.
  2. Pop, Eric. Self-heating and scaling of thin body transistors. stanford university, 2005.
  3. Vasileska, D. "Direct Solution of Boltzmann Transport Equation: Monte Carlo Method." Arizon State University.