晶格温度和载流子温度

从Sentaurus可以看到最主流的半导体器件仿真中是如何处理温度的，Sentaurus可以计算三种不同的温度，晶格温度、电子温度、和空穴温度。在半导体中，热量是通过热电子和晶格碰撞（发射声子）产生的，当半导体器件的制程并不是太小时，高能电子从源极跑向漏极的时候已经撞了很多次，局域电子温度和晶格温度之间已经达到了平衡，电子温度=空穴温度=晶格温度。而对于深亚微米器件，电子可能没经过什么碰撞就跑了，此时局域电子能量和晶格能量间是不平衡的，这种非平衡效应使得电子温度、空穴温度和晶格温度间是不相等的。

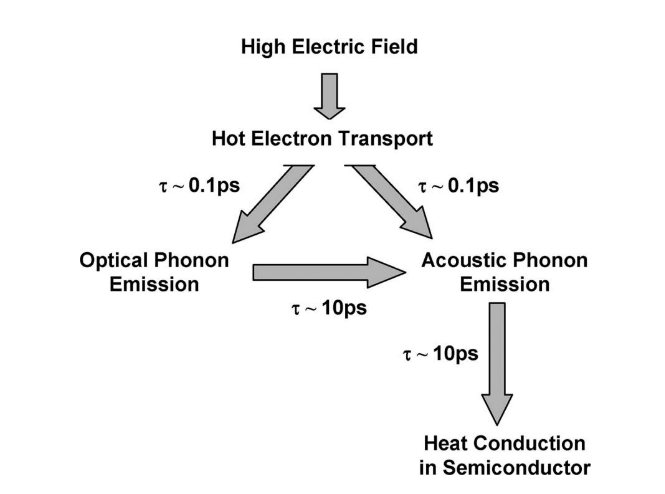
从粗糙到复杂，Sentaurus中有几种温度计算的方法：

• 假设器件的晶格温度分布是均匀的，计算器件总的产热，然后得到器件的平均温度
• 使用热力学模型或者水动力学模型求解非均匀的晶格温度分布
• 使用水动力学模型求解载流子的温度

求解晶格温度时，需要设置热边界条件（等温/绝热边界），因为它本质上就是用傅里叶定律在解温度场；求解载流子温度时，不需要设置热边界条件，因为载流子的运动本质上是受电学部分控制的，这个温度只是对局域载流子能量的一种描述，比如电子迁移率越高，电子跑的越快，动能越大，电子温度也就越高。

Uniform Self-Heating

Chen X, Boumaiza S, Wei L. Self-heating and equivalent channel temperature in short gate length GaN HEMTs[J]. IEEE transactions on electron devices, 2019, 66(9): 3748-3755.

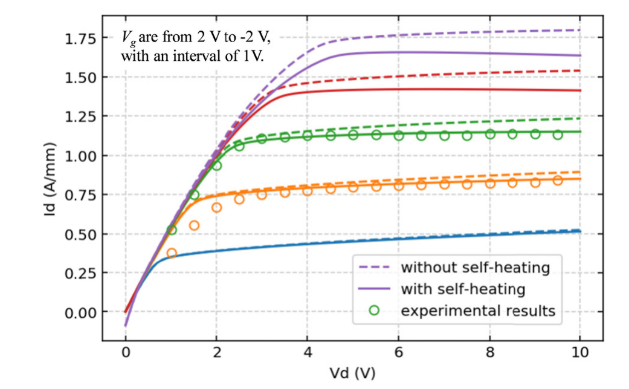
这是处理Self-Heating的比较简单的方式，Self-Heating效应可以理解为器件内的温升引起的器件性能的下降。最直观的，就是同一个Drain电压下，器件的输出电流变小了。如果我们关注的只是电学性能，那么我们实际上只需要引入一个等效温度就可以描述这种器件输出电流的降低了。比如理想情况下整个器件都是300K，得到的理想输出电流为1，电热耦合仿真给出的实际电流为0.9，此时我可以将整个器件的等效温度设置为350K，在350K下得到的输出电流就变成0.9了。通过建立等效温度的对应关系，我们可以用这种简单的方法考虑自热效应引起的电学性能退化，上面这篇文章讨论的就是这个问题，不过作者已经不在学术圈去Sentaurus工作，联系不到了..

Thermodynamic Model for Lattice Temperature

Chatterjee B, Dundar C, Beechem T E, et al. Nanoscale electro-thermal interactions in AlGaN/GaN high electron mobility transistors[J]. Journal of Applied Physics, 2020, 127(4): 044502.

\[ \begin{aligned} \frac{\partial}{\partial t}\left(c_{\mathrm{L}} T\right)-\nabla \cdot(\kappa \nabla T)=&-\nabla \cdot\left[\left(P_{n} T+\Phi_{n}\right) \vec{J}_{n}+\left(P_{p} T+\Phi_{p}\right) \vec{J}_{p}\right] \\ &-\frac{1}{q}\left(E_{\mathrm{C}}+\frac{3}{2} k T\right)\left(\nabla \cdot \vec{J}_{n}-q R_{\mathrm{net}, n}\right) \\ &-\frac{1}{q}\left(-E_{\mathrm{V}}+\frac{3}{2} k T\right)\left(-\nabla \cdot \vec{J}_{p}-q R_{\mathrm{net}, p}\right)+\hbar \omega G^{\mathrm{opt}} \end{aligned} \]

在SDEVICE脚本中的Physics部分开启Thermodynamic，Sentaurus就会用thermodynamic模型计算晶格温度，上面这篇文章里特别提到了这个thermodynamic model。这个方程看起来复杂，但是实际上很好理解，左侧分别是非稳态项和导热项，导热项使用傅里叶定律。右侧全部是热源项，不同项对应着不同机制。

第一项是焦耳热和汤姆逊热，实际上就是由于塞贝克效应，温度场的不均匀性会产生一个附加电动势， \[ \begin{aligned} &\vec{J}_{n}=-n q \mu_{n}\left(\nabla \Phi_{n}+P_{n} \nabla T\right) \\ &\vec{J}_{p}=-p q \mu_{p}\left(\nabla \Phi_{p}+P_{p} \nabla T\right) \end{aligned} \] 分别是电子和空穴电流，\(\Phi_n\)和\(\Phi_p\)分别是电子和空穴的准费米能级，第一项就是用爱因斯坦关系简化后的扩散漂移模型（DDM），原始的DDM模型中电流可以拆成扩散项和漂移项两项， \[ \begin{aligned} &\vec{J}_{n}=\mu_{n}\left(n \nabla E_{\mathrm{C}}-1.5 n k T \nabla \ln m_{n}\right)+D_{n}\left(\nabla n-n \nabla \ln \gamma_{n}\right) \\ &\vec{J}_{p}=\mu_{p}\left(p \nabla E_{\mathrm{V}}+1.5 p k T \nabla \ln m_{p}\right)-D_{p}\left(\nabla p-p \nabla \ln \gamma_{p}\right) \end{aligned} \] 第一项是电场作用下的运动，第二项是浓度梯度作用下的扩散。在爱因斯坦关系下，\(D_n = kT\mu_n, D_p = kT\mu_p\)，此时方程可以化简成 \[ \begin{aligned} &\vec{J}_{n}=-n q \mu_{n} \nabla \Phi_{n} \\ &\vec{J}_{p}=-p q \mu_{p} \nabla \Phi_{p} \end{aligned} \] thermodynamic模型相比于DDM额外加上了一项由温差产生的电流，\(P_n\)和\(P_p\)分别是电子和空穴的帕尔贴系数。在不考虑温度场的时候，自然也就不存在温度场梯度，这一项也就不存在了。考虑温差电动势后，电动势和电流均要额外补充温差电项，这也就是第一项的形式。

第二项和第三项分别是局域电子和空穴的能量净生成量，电流的散度是净流入/流出多少电子，\(R_{\text{net}}\)是当地的电子的复合率，即生成或湮灭多少电子，前面\(E_c\)是当地的导带能量，即近似可以认为是当地电子所具有的势能，\(3/2kT\)是电子的动能，因此\(E_C+3/2kT\)就是当地一个电子的总能量，\(\left(\nabla \cdot \vec{J}_{n}-q R_{\mathrm{net}, n}\right)/q\)是当地电子的净生成数目，加起来就是能量的净生成量。

最后一项是生成光子的能量，\(G^{\text{opt}}\)是光子生成率。

在稳态情况下，局域的电子和空穴数目达到平衡，既不会增多，也不会减少，根据电子和空穴的连续性方程， \[ \nabla \cdot \vec{J}_{n}=q R_{\text {net }, n}+q \frac{\partial n}{\partial t} \quad-\nabla \cdot \vec{J}_{p}=q R_{\text {net }, p}+q \frac{\partial p}{\partial t} \] 第二项和第三项消失，总产热退化为， \[ H=-\nabla \cdot\left[\left(P_{n} T+\Phi_{n}\right) \vec{J}_{n}+\left(P_{p} T+\Phi_{p}\right) \vec{J}_{p}\right]+h \omega G^{\mathrm{opt}} \] 其中电子部分可以整理为， \[ -\nabla \cdot\left[\left(P_{n} T+\Phi_{n}\right) \vec{J}_{n}\right]=\frac{1}{q n \mu_{n}}\left|\vec{J}_{n}\right|^{2}-q T \nabla P_{n}\cdot \vec{J}_{n}+\left[\left(P_{n} T+\Phi_{n}\right) \vec{J}_{n} \cdot n_{S}\right]_{S} \delta_{S}-q\left(P_{n} T+\Phi_{n}\right) R_{\mathrm{net}, n} \] 由左到右四项分别是电子的焦耳热、汤姆逊热、帕尔贴热、重组热，对于N型MOSFET而言，电子焦耳热占据了绝大部分，只考虑第一项也没什么影响。

Thermodynamic Model for Lattice Temperatures

我们可以这样理解流动传热中的能量方程，它本质上是一个能量守恒方程，即局域能量净增加量=净热流量+净热源项，只不过局域能量通过比热容和温度对应，而此时方程不封闭，我们此时需要一个模型来建立热流和温度的关系，于是傅里叶模型出现了，它假定热流和温度梯度成正比，这个比例系数是热导率。实际上傅里叶定律只是对热流满足关系的一种假设，它只在宏观情况下成立，通过对玻尔兹曼方程做积分，我们可以得到如下形式的连续方程、动量方程及能量方程， \[ \begin{gathered} \frac{\mathrm{d} \rho}{\mathrm{d} t}+\rho \frac{\partial v_{k}}{\partial x_{k}}=0, \\ \rho \frac{\mathrm{d} v_{i}}{\mathrm{~d} t}+\theta \frac{\partial \rho}{\partial x_{i}}+\rho \frac{\partial \theta}{\partial x_{i}}+\frac{\partial \sigma_{i k}}{\partial x_{k}}=0, \\ \frac{3}{2} \rho \frac{\mathrm{d} \theta}{\mathrm{d} t}+\rho \theta \frac{\partial v_{k}}{\partial x_{k}}+\frac{\partial q_{k}}{\partial x_{k}}+\sigma_{k l} \frac{\partial v_{k}}{\partial x_{l}}=0, \end{gathered} \] 方程中有粘性应力张量\(\sigma\)和热流密度\(q\)，我们可以在给定线性碰撞算子的前提下用矩方法推导出更高阶的粘性应力张量和热流的表达式代替牛顿定律和傅里叶定律，比如在R13方程框架下，粘性应力张量和热流满足如下方程， \[ \begin{aligned} &\frac{\mathrm{d} \sigma_{i j}}{\mathrm{~d} t}+\sigma_{i j} \frac{\partial v_{k}}{\partial x_{k}}+\frac{4}{5} \frac{\partial q_{(i}}{\partial x_{j\rangle}}+2 \rho \theta \frac{\partial v_{\langle i}}{\partial x_{j\rangle}}+2 \sigma_{k\langle i} \frac{\partial v_{j\rangle}}{\partial x_{k}}+\frac{\partial m_{i j k}^{(\eta)}}{\partial x_{k}}=\Sigma_{i j}^{(\eta, 1)}+\Sigma_{i j}^{(\eta, 2)}, \\ &\frac{\mathrm{d} q_{i}}{\mathrm{~d} t}+\frac{5}{2} \rho \theta \frac{\partial \theta}{\partial x_{i}}+\frac{5}{2} \sigma_{i k} \frac{\partial \theta}{\partial x_{k}}+\theta \frac{\partial \sigma_{i k}}{\partial x_{k}}-\theta \sigma_{i k} \frac{\partial \ln \rho}{\partial x_{k}}+\frac{7}{5} q_{k} \frac{\partial v_{i}}{\partial x_{k}} \\ &\quad+\frac{2}{5} q_{k} \frac{\partial v_{k}}{\partial x_{i}}+\frac{7}{5} q_{i} \frac{\partial v_{k}}{\partial x_{k}}-\frac{\sigma_{i j}}{\rho} \frac{\partial \sigma_{j k}}{\partial x_{k}} \\ &\quad+C^{(\eta)}\left(\sigma_{i k} \frac{\partial \theta}{\partial x_{k}}+\theta \frac{\partial \sigma_{i k}}{\partial x_{k}}\right)+\frac{1}{2} \frac{\partial R_{i k}^{(\eta)}}{\partial x_{k}}+\frac{1}{6} \frac{\partial \Delta^{(\eta)}}{\partial x_{i}}+m_{i j k}^{(\eta)} \frac{\partial v_{j}}{\partial x_{k}}=Q_{i}^{(\eta, 1)}+Q_{i}^{(\eta, 2)}, \end{aligned} \] 方程组共有密度、温度、速度分量、应力分量及热流密度分量共13个独立变量，在给定了高阶矩和碰撞项以低阶矩表示的形式后，方程封闭。

我们可以这样理解半导体中求解的这几个方程，根本上我们要求解泊松方程和电流连续性方程，泊松方程是电通量守恒方程，电流连续性方程是也是守恒方程，他们都是自然满足的，但此时方程不封闭，我们需要模型来封闭我们的方程。所以我们说DDM不是方程，而是一个模型，这个模型假设给出了电流的表达式，建立了电流和电场、载流子浓度分布间的关系，就像傅里叶定律建立了热流和温度场之间的关系一样。傅里叶定律在载流子自由程和体系尺寸相当时不成立，我们需要引入更高阶的假设，所以DDM不足以完全描述深亚微米器件，我们需要引入更高阶的模型，即hydrodynamic水动力学模型，实际上thermodynamic模型也可以这样理解。在水动力学模型中，电流的表达式为， \[ \begin{aligned} &\vec{J}_{n}=\mu_{n}\left(n \nabla E_{\mathrm{C}}+k T_{n} \nabla n-n k T_{n} \nabla \ln \gamma_{n}+\lambda_{n} f_{n}^{\mathrm{td}} k n \nabla T_{n}-1.5 n k T_{n} \nabla \ln m_{n}\right) \\ &\vec{J}_{p}=\mu_{p}\left(p \nabla E_{\mathrm{V}}-k T_{p} \nabla p+p k T_{p} \nabla \ln \gamma_{p}-\lambda_{p} f_{p}^{\mathrm{td}} k p \nabla T_{p}+1.5 p k T_{p} \nabla \ln m_{p}\right) \end{aligned} \] 其中四项和DDM中一样，只是此时的温度不再是晶格温度而是载流子温度了，多了一项由载流子温度梯度引起的电流贡献，就像热电效应一样。此外，这里多了两个载流子温度，我们还需要引入载流子温度的能量守恒方程， \[ \begin{gathered} \frac{\partial W_{n}}{\partial t}+\nabla \cdot \vec{S}_{n}=\vec{J}_{n} \cdot \nabla E_{\mathrm{C}} / q+\left.\frac{d W_{n}}{d t}\right|_{\text {coll }}\\ \frac{\partial W_{p}}{\partial t}+\nabla \cdot \vec{S}_{p}=\vec{J}_{p} \cdot \nabla E_{\mathrm{V}} / q+\left.\frac{d W_{p}}{d t}\right|_{\text {coll }} \\ \frac{\partial W_{\mathrm{L}}}{\partial t}+\nabla \cdot \vec{S}_{\mathrm{L}}=\left.\frac{d W_{\mathrm{L}}}{d t}\right|_{\text {coll }} \end{gathered} \] 对于能量流，我们还需要给出新的近似， \[ \begin{gathered} \vec{S}_{n}=-\frac{5 r_{n} \lambda_{n}}{2}\left(\frac{k T_{n} }{q}\vec{J_n}+f_{n}^{\mathrm{hf}} \hat{\kappa}_{n} \nabla T_{n}\right) \\ \vec{S}_{p}=-\frac{5 r_{p} \lambda_{p}}{2}\left(\frac{-k T_{p}}{q} \vec{J_{p}}+f_{p}^{\mathrm{hf}} \hat{\kappa}_{p} \nabla T_{p}\right) \\ \vec{S}_{\mathrm{L}}=-\kappa_{\mathrm{L}:} \nabla T_{\mathrm{L}} \\ \hat{\kappa}_{n}=\frac{k^{2}}{q} n \mu_{n} T_{n} \\ \hat{\kappa}_{p}=\frac{k^{2}}{q} p \mu_{p} T_{p} \end{gathered} \] 具体的推导有点麻烦.. 但大致的逻辑和图像是这样。