五点差分格式的构造
五点差分格式的构造
泊松方程,描述了含源系统稳态扩散过程的分布,比如静电场方程或者含内热源的导热方程, \[ - \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) = f \] 用数值差商代替微商,可以得到微分方程对应的差分方程: \[ 4u_{i,j} - u_{i+1, j} - u_{i-1, j} - u_{i, j+1} - u_{i, j-1} = h^2f_{i, j} \] 数值求解微分方程本质上等同于求解一个线性方程组, \[ A\boldsymbol{u} = \boldsymbol{b} \] 线性方程组有唯一解,即需要有效的方程组个数等于未知量个数. 在差分方程的求解过程中,每一个离散的节点都相当于一个未知量,因此每一个节点都需要一个对应的线性方程,才能保证方程组封闭. 在泊松方程的五点差分格式中,每一个节点对应的线性方程都是上面那个离散出的差分方程,边界节点差分方程的表达式也是在它的基础上得到的,在后面的section分不同情况讨论一下.

我们把网格点按照自左至右、自下而上的自然次序排列,可以得到 \[ \begin{equation} \begin{aligned} \boldsymbol{u} &=\left(u_{11}, u_{21}, \cdots, u_{N 1}, \cdots, u_{N 2}, \cdots, u_{1 N}, \cdots, u_{N N}\right)^{T} \\ \boldsymbol{b} &=h^{2}\left(f_{11}, \cdots, f_{N 1}, f_{12}, \cdots, f_{N 2}, \cdots, f_{1 N}, \cdots, f_{N N}\right) \end{aligned} \end{equation} \] 有\(N\)个节点,就有\(N\)个方程组,相当于\(\boldsymbol{u}\)就是一个\(N\)维向量,而\(A\)就是一个\(N\times N\)阶的矩阵,\(A\)和\(\boldsymbol{u}\)的每一行相乘,就代表了一个方程组. 现在要求解这个线性方程组,唯一要做的就是确定矩阵\(A\)的系数. 以\(3\times 3\)的情况为例,
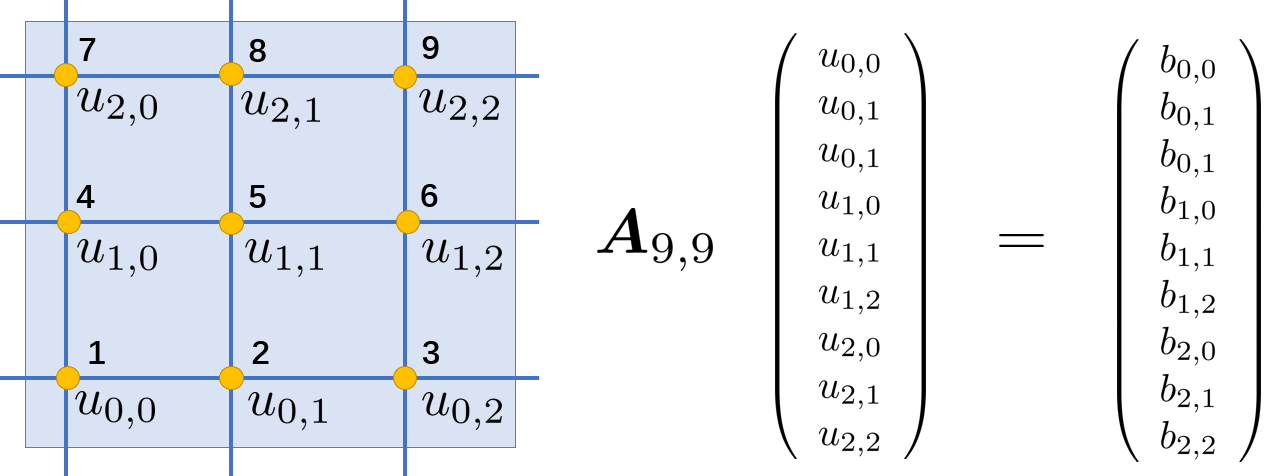
\(u_{i, j}\)这一行就对应着以\(u_{i, j}\)为中心的五点差分方程,也就是\(A\)的第\(i\times N+j\)行和整个\(\boldsymbol{u}\)向量相乘. 比如\(u_{1, 1}\)对应的五点差分方程,就对应着\(A_{4, \ldots}\)这一行(行、列的索引从0开始定义). 于是我们就得到了行索引的对应关系,以\(u_{i, j}\)为中心的五点差分方程余下的系数,对应着\(A_{i\times N+j, \ldots}\)这一行的列索引. 根据矩阵乘法的对应关系,我们可以得到 \[ \begin{aligned} &\text{row} = i\times N + j\\ &u_{i, j} \rightarrow A_{\text{row}, \text{row}}\\ &u_{i+1, j} \rightarrow A_{\text{row}, \text{row} + N}\\ &u_{i-1, j} \rightarrow A_{\text{row}, \text{row} - N}\\ &u_{i, j+1} \rightarrow A_{\text{row}, \text{row} + 1}\\ &u_{i, j-1} \rightarrow A_{\text{row}, \text{row} - 1}\\ \end{aligned} \] \(u_{i, j}\)上面的节点,就是在行标的基础上加一个格点总列数\(N\),下面的节点就是减去\(N\),左边的节点\(-1\),右面的节点\(+1\),于是内节点对应的矩阵\(A\)的系数,就是 \[ \begin{aligned} &A_{\text{row}, \text{row}} = 4\\ &A_{\text{row}, \text{row}+N} = -1\\ &A_{\text{row}, \text{row}-N} = -1\\ &A_{\text{row}, \text{row}+1} = -1\\ &A_{\text{row}, \text{row}-1} = -1\\ \end{aligned} \] 通过一个遍历循环,我们可以得到矩阵\(A\)所有位置的系数,之后就可以解这个线性方程组了. 下面讨论一下边界节点的处理方式.
第一类边界条件
当一圈的边界值都是第一类边界条件时处理比较容易,我们不需要列出边界节点的方程,因此比如对于上方\(3\times 3\)的网格,这9个节点都是内节点. 此时左上角的角点对应的差分方程,只要把边界值挪到等式右侧就可以了,左侧不存在对应节点系数. \[ 4u_{i,j} - u_{i-1, j} - u_{i, j+1} = h^2f_{i, j} + u_{\text{上方边界}} + u_{\text{左侧边界}} \] 这个时候得到的是这样的矩阵:

1 | N = 40 |

第二、三类边界条件
对于第二类或者第三类边界条件,这时边界节点的值也是未知的,我们在求解时需要求解边界节点. 以左边界为例,我们可以列出这个边界节点的五点差分方程, \[ 4u_{i,j} - u_{i+1, j} - u_{i-1, j} - u_{i, j+1} - u_{i, j-1} = h^2f_{i, j} \] 此时\(u_{i, j-1}\)是不存在的,但是我们可以把它当作虚拟节点,来构造边界条件的中心差分,这种构造方式保留了二阶精度. 比如对于绝热边界条件, \[ \frac{\partial u}{\partial x} = 0 \] 其差分方程为 \[ \frac{u_{i, j+1} - u_{j-1}}{2h} = 0 \] 实际上意味着左边界节点两侧的节点值相等,因此五点差分格式变为 \[ 4u_{i,j} - u_{i+1, j} - u_{i-1, j} - 2u_{i, j+1} = h^2f_{i, j} \] 对应的矩阵系数变为 \[ \begin{aligned} &A_{\text{row}, \text{row}} = 4\\ &A_{\text{row}, \text{row}+N} = -1\\ &A_{\text{row}, \text{row}-N} = -1\\ &A_{\text{row}, \text{row}+1} = -2\\ \end{aligned} \] 对于对流换热边界条件(这里全部无量纲化), \[ \frac{\partial u}{\partial x} = -u \] 其差分方程为 \[ \frac{u_{i, j+1} - u_{j-1}}{2h} = -u \] 代回边界节点的五点差分格式中,可以得到 \[ (4+2h)u_{i,j} - u_{i+1, j} - u_{i-1, j} - 2u_{i, j+1} = h^2f_{i, j} \] 于是 \[ \begin{aligned} &A_{\text{row}, \text{row}} = 4+2h\\ &A_{\text{row}, \text{row}+N} = -1\\ &A_{\text{row}, \text{row}-N} = -1\\ &A_{\text{row}, \text{row}+1} = -2\\ \end{aligned} \] 对于角点,其矩阵系数就是两个边界条件的叠加. 比如对于下面这个问题,
在\(D=\{(x, y) \mid 0 \leq x, y \leq 1\}\)上给出边值问题 $$ { \[\begin{array}{l} -\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right)=16, \quad 0<x, y<1 \\ \left.u\right|_{x=1}=0,\left.\quad \frac{\partial u}{\partial y}\right|_{y=1}=-u \\ \left.\frac{\partial u}{\partial x}\right|_{x=0}=0,\left.\quad \frac{\partial u}{\partial y}\right|_{y=0}=0 \end{array}\]. $$ 这个边值问题描述了含有均匀内热源的正方形体系,左侧和下侧绝热,上侧对流换热,右侧与低温热沉相接触的导热问题. 我们分别引入一层边界节点,此时左、上、下边界节点代表边界值,而右侧仍然是内节点.

1 | N = 40 |
