扩展热阻(3)-多层器件
多层器件的热阻分析
Bagnall K R, Muzychka Y S, Wang E N. Analytical solution for temperature rise in complex multilayer structures with discrete heat sources[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2014, 4(5): 817-830.
Problem Statement
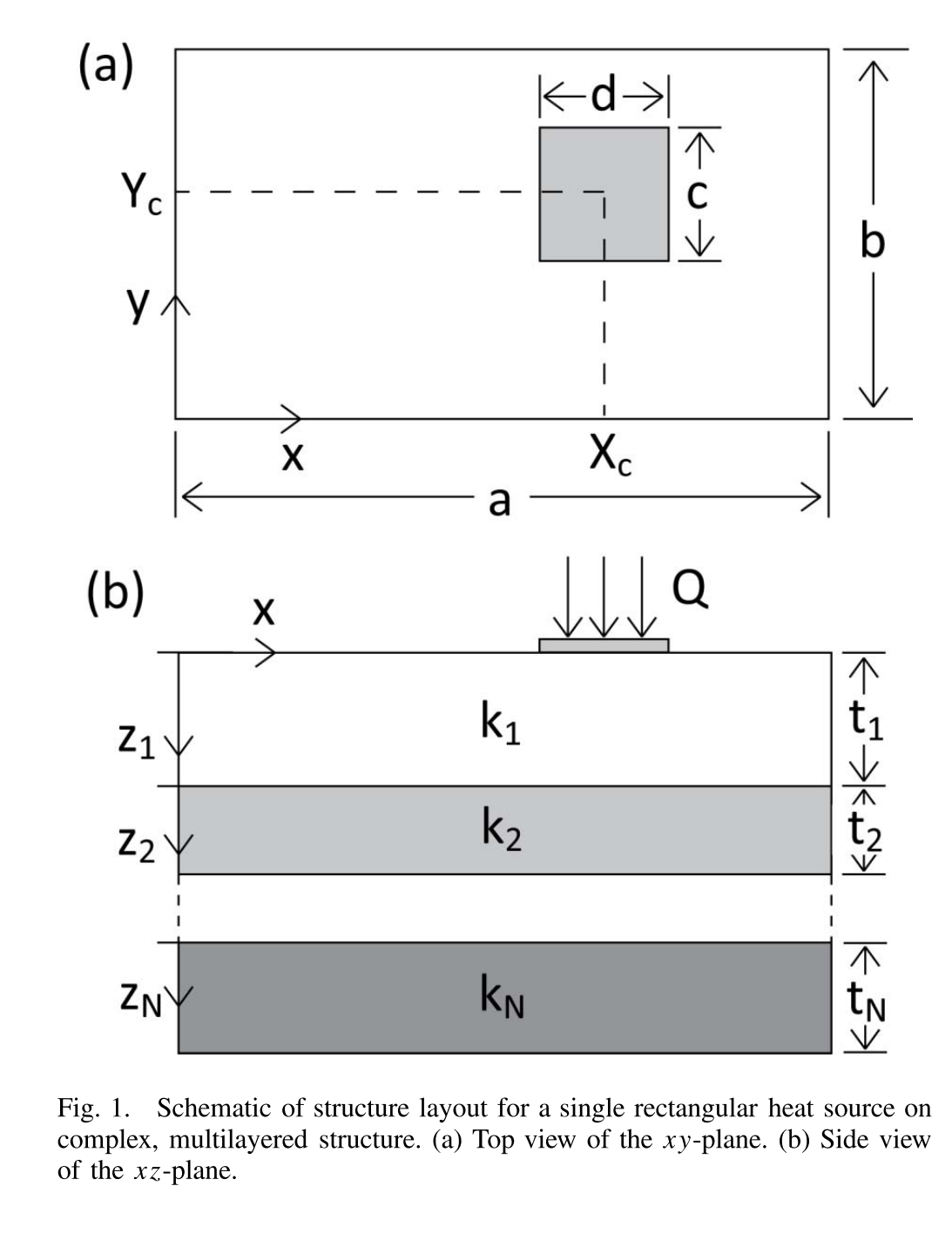
控制方程,
\[ \nabla^{2} \theta=\frac{\partial^{2} \theta}{\partial x^{2}}+\frac{\partial^{2} \theta}{\partial y^{2}}+\frac{\partial^{2} \theta}{\partial z^{2}}=0 \]
顶层热源区域的边界条件,
\[ -\left.k_{1} \frac{\partial \theta_{1}}{\partial z_{1}}\right|_{z_{1}=0}=q = Q/cd \]
下标代表第几层,其中\(1\)为最上层热源平面,\(N\)为最底层对流换热或者热沉平面,\(j\)代表中间层。之前求过单层的扩展热阻解析解,在处理多层时,实际上各层的解的形式基本还是一样的,只不过底部的边界形式有一些差别。所以处理这种多层问题,基本思路是按照单层求解的方式,对每一层分别求解,然后处理边界的耦合问题。因此求解的不是整个的\(\theta\),而是各层的\(\theta_j\),对每一层来说,它\(z\)方向可取的值就是从\(0\)开始到\(t_j\)结束。因此\(z_j = 0\)代表第\(j-1\)层和第\(j\)层的界面,\(z_j = t_j\)代表第\(j\)层和第\(j+1\)层的界面。
顶层其他区域的边界条件,
\[ -\left. \frac{\partial \theta_{1}}{\partial z_{1}}\right|_{z_{1}=0}=0 \]
侧边界绝热边界条件,
\[ \begin{aligned} &\left.\frac{\partial \theta_j}{\partial x}\right|_{x=0, a}=0 \\ &\left.\frac{\partial \theta_j}{\partial y}\right|_{y=0, b}=0 \end{aligned} \]
底层(第\(N\)层)为对流换热边界条件,
\[ k_N\left.\frac{\partial \theta_N}{\partial z_N}\right|_{z=t_{N}}=-\frac{h_s}{k_{N}}\theta \left(x, y, t_{N}\right) \]
\(h_s\)是底部的对流换热系数,当\(h_s\rightarrow\infty\)时,底部退化为热沉边界条件。
对于层间的边界条件,当理想界面(无界面热阻时),满足温度和热流连续条件,
\[ \begin{aligned} &\theta_{j}\left(x, y, t_{j}\right)=\theta_{j+1}(x, y, 0) \\ &\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=\left.k_{j+1} \frac{\partial \theta_{j+1}}{\partial z_{j+1}}\right|_{z_{j+1}=0} \end{aligned} \]
当存在界面热阻时,此时热流连续,温度会在界面发生跳跃,
\[ \begin{aligned} &-\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=h_{c j}\left[\theta_{j}\left(x, y, t_{j}\right)-\theta_{j+1}(x, y, 0)\right] \\ &\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=\left.k_{j+1} \frac{\partial \theta_{j+1}}{\partial z_{j+1}}\right|_{z_{j+1}=0} \end{aligned} \]
\(h_c\)被称为界面热导,它的值被定义为界面的热流与两侧温差的比值。
General Solution
具体分离变量的解法已经总结在前面的文章里了(矩形偏心热源的扩展热阻模型),每一层通解的形式满足,
\[ \begin{aligned} \theta_{j}\left(x, y, z_{j}\right)=& A_{0 j}+B_{0 j} z+\sum_{m=1}^{\infty} \cos \left(\lambda_{m} x\right)\left[A_{1 j} \cosh \left(\lambda_{m} z_{j}\right)+B_{1 j} \sinh \left(\lambda_{m} z_{j}\right)\right] \\ &+\sum_{n=1}^{\infty} \cos \left(\delta_{n} y\right)\left[A_{2 j} \cosh \left(\delta_{n} z_{j}\right)+B_{2 j} \sinh \left(\delta_{n} z_{j}\right)\right] \\ &+\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} \cos \left(\lambda_{m} x\right) \cos \left(\delta_{n} y\right)\left[A_{3 j} \cosh \left(\beta_{m n} z_{j}\right)+B_{3 j} \sinh \left(\beta_{m n} z_{j}\right)\right] \end{aligned} \]
其中
\[ \lambda = m\pi/a, \sigma = n\pi/b, \beta = \sqrt{\lambda^2 + \sigma^2} \]
同样,定义各层的扩展函数,
\[ \phi_j(\gamma_n) \equiv -\frac{B_{ij}}{A_{ij}} \]
\(\gamma_n\)分别代表\(x,y,z\)方向展开的特征值\(\lambda_m, \delta_n, \beta_{mn}\),其中\(i\)代表是第几组无穷级数的系数,\(j\)代表是第几层。扩展函数的值可以用每一层的底部边界条件来确定。
对于底部边界,
\[ k_N\left.\frac{\partial \theta_N}{\partial z_N}\right|_{z=t_{N}}=-\frac{h_s}{k_{N}}\theta \left(x, y, t_{N}\right) \]
代入无穷级数通解可以得到,
\[ \phi_{N}\left(\gamma_{n}\right)=-\frac{B_{i N}}{A_{i N}}=\frac{\frac{k_{N} \gamma_{n}}{h_{s}} \tanh \left(\gamma_{n} t_{N}\right)+1}{\frac{k_{N} \gamma_{n}}{h_{s}}+\tanh \left(\gamma_{n} t_{N}\right)} \]
对于第\(j\)层的扩展函数,可以用\(j+1\)层的扩展函数递归得到,下面分是否考虑界面热阻两种情况讨论。
无界面热阻
对于第\(j\)层和第\(j+1\)层的界面,满足,
\[ \begin{aligned} &\theta_{j}\left(x, y, t_{j}\right)=\theta_{j+1}(x, y, 0) \\ &\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=\left.k_{j+1} \frac{\partial \theta_{j+1}}{\partial z_{j+1}}\right|_{z_{j+1}=0} \end{aligned} \]
代入无穷级数解,可以得到,
\[ \begin{aligned} A_{i,j} \cosh(\beta t_j) + B_{i,j}\sinh (\beta t_j) &= A_{i,j+1}\\ k_j \left[ A_{i,j}\sinh(\beta t_j) + B_{i,j} \cosh(\beta t_j) \right] &= k_{j+1}B_{i,j+1} \\ \end{aligned} \]
代入
\[ \begin{aligned} \phi_j(\gamma_n) &= -\frac{B_{ij}}{A_{ij}} \\ \phi_{j+1}(\gamma_n) &= -\frac{B_{i,j+1}}{A_{i,j+1}} \\ \end{aligned} \]
得到,
\[ \begin{aligned} A_{i,j} \left[ \cosh(\beta t_j) +\phi_j(\gamma_n)\sinh (\beta t_j)\right] &= A_{i,j+1}\\ k_j A_{i, j} \left[ \sinh(\beta t_j) +\phi_j(\gamma_n) \cosh(\beta t_j) \right] &= -k_{j+1}A_{i,j+1}\phi_{j+1}(\gamma_n) \\ \end{aligned} \]
上下两式相除,得到,
\[ \phi_{j}\left(\gamma_{n}\right)=-\frac{B_{i j}}{A_{i j}}=\frac{\frac{k_{j}}{k_{j+1}} \tanh \left(\gamma_{n} t_{j}\right)+\phi_{j+1}\left(\gamma_{n}\right)}{\frac{k_{j}}{k_{j+1}}+\phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)} \]
\(\phi_1(\gamma_n)\)可以通过\(\phi_2(\gamma_n)\)来求解,\(\phi_2(\gamma_n)\)可以通过\(\phi_3(\gamma_n)\)来求解..最后可以通过热沉平面递归得到所有的扩展函数。
热源平面的温度分布为,
\[ \begin{aligned} \theta_{1}(x, y, 0)=& A_{01}+\sum_{m=1}^{\infty} A_{11} \cos \left(\lambda_{m} x\right)+\sum_{n=1}^{\infty} A_{21} \cos \left(\delta_{n} y\right) \\ &+\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{31} \cos \left(\lambda_{m} x\right) \cos \left(\delta_{n} y\right) \end{aligned} \]
按照同样的方法(矩形偏心热源的扩展热阻模型),在热源平面作傅里叶级数展开,可以得到\(Ai1\)同样的表达式,只不过此时扩展函数发生了变化,
\[ \begin{aligned} A_{11}&=\frac{4 Q \cos \left(\lambda_{m} X_{c}\right) \sin \left(\frac{1}{2}\lambda_m c\right)}{a b c k_{1} \lambda_{m}^{2} \phi_1 \left(\lambda_{m}\right)}\\ A_{21}&=\frac{4 Q \cos \left(\delta_{n} Y_{c}\right) \sin \left(\frac{1}{2}\delta_n d\right)}{a b d k_{1} \delta_{n}^{2} \phi_1 \left(\delta_{n}\right)}\\ A_{31}&=\frac{16 Q \cos \left(\lambda_{m} X_{c}\right) \sin \left(\frac{1}{2}\lambda_m c\right) \cos \left(\delta_{n} Y_{c}\right) \sin \left(\frac{1}{2}\delta_n d\right)}{a b c d k_{1}\lambda_{m} \delta_{n} \beta_{\mathrm{mn}} \phi_1 \left(\beta_{\mathrm{mn}}\right)}\\ \end{aligned} \]
线性部分的解为,
\[ \begin{aligned} A_{01} &=\frac{Q}{a b}\left(\frac{1}{h_{s}}+\sum_{l=1}^{N} \frac{t_{l}}{k_{l}}\right) \\ B_{01} &=-\frac{Q}{a b k_{1}} \end{aligned} \]
各层的温度分布为,
\[ \begin{aligned} \theta_{j}\left(x, y, z_{j}\right)=& A_{0 j}+B_{0 j} z+\sum_{m=1}^{\infty} A_{1 j} \cos \left(\lambda_{m} x\right)\left[\cosh \left(\lambda_{m} z_{j}\right)-\phi_{j}\left(\lambda_{m}\right) \sinh \left(\lambda_{m} z_{j}\right)\right] \\ &+\sum_{n=1}^{\infty} A_{2 j} \cos \left(\delta_{n} y\right)\left[\cosh \left(\delta_{n} z_{j}\right)-\phi_{j}\left(\delta_{n}\right) \sinh \left(\delta_{n} z_{j}\right)\right] \\ &+\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} A_{3 j} \cos \left(\lambda_{m} x\right) \cos \left(\delta_{n} y\right)\left[\cosh \left(\beta_{m n} z_{j}\right)-\phi_{j}\left(\beta_{m n}\right) \sinh \left(\beta_{m n} z_{j}\right)\right] \end{aligned} \]
按照反向求\(\phi_j(\gamma_n)\)的关系式正向递归,此时可以建立\(A_{i, j}\)和\(A_{i, j-1}\)之间的联系,
\[ A_{i j}=A_{i, j-1}\left[\cosh \left(\gamma_{n} t_{j-1}\right)-\phi_{j-1}\left(\gamma_{n}\right) \sinh \left(\gamma_{n} t_{j-1}\right)\right] \]
对于零阶傅里叶系数实际上就是\(\theta_0 = QR_{1D}\),其中\(A_{0j}\)为温度的截距部分,每一层都要做一个偏置, \[ A_{0 j}=\frac{Q}{a b}\left(\frac{1}{h_{s}}+\sum_{l=j}^{N}\frac{t_{l}}{k_{l}}\right) \] 斜率部分和每层的热导率有关, \[ B_{0 j}=-\frac{Q}{a b k_{j}} \] 于是通过一反一正两个递归,最终可以得到整个系统中的温度分布。
考虑界面热阻
当考虑界面热阻时,解的形式是完全一样的,唯一要做的就是对扩展函数作出修改,而且考虑界面热阻后的扩展函数应该是可以退化成不考虑界面热阻时的结果的
用含界面热阻的边界条件重新推导一下扩展函数的递推关系,
\[ \begin{aligned} &-\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=h_{c j}\left[\theta_{j}\left(x, y, t_{j}\right)-\theta_{j+1}(x, y, 0)\right] \\ &\left.k_{j} \frac{\partial \theta_{j}}{\partial z_{j}}\right|_{z_{j}=t_{j}}=\left.k_{j+1} \frac{\partial \theta_{j+1}}{\partial z_{j+1}}\right|_{z_{j+1}=0} \end{aligned} \]
代入无穷级数解,可以得到,
\[ \begin{aligned} - \gamma_n k_j \left[ A_{i,j}\sinh(\gamma_n t_j) + B_{i,j} \cosh(\gamma_n t_j) \right] &= h_{cj}\left[ A_{i,j} \cosh(\gamma_n t_j) + B_{i,j}\sinh (\gamma_n t_j) - A_{i,j+1} \right]\\ k_j \left[ A_{i,j}\sinh(\gamma_n t_j) + B_{i,j} \cosh(\gamma_n t_j) \right] &= k_{j+1}B_{i,j+1} \\ \end{aligned} \]
代入,
\[ \begin{aligned} \phi_j(\gamma_n) &= -\frac{B_{ij}}{A_{ij}} \\ \phi_{j+1}(\gamma_n) &= -\frac{B_{i,j+1}}{A_{i,j+1}} \\ \end{aligned} \]
得到,
\[ \begin{aligned} - \gamma_n k_j A_{ij} \left[\sinh(\gamma_n t_j) -\phi_j(\gamma_n) \cosh(\gamma_n t_j) \right] &= h_{cj}A_{i,j}\left[ \cosh(\gamma_n t_j) -\phi_j(\gamma_n)\sinh (\gamma_n t_j)\right] - h_{cj}A_{i,j+1} \\ - \gamma_nk_j A_{i,j} \left[\sinh(\gamma_n t_j) -\phi_j(\gamma_n) \cosh(\gamma_n t_j) \right] &= k_{j+1}\phi_{j+1}(\gamma_n)A_{i,j+1} \\ \end{aligned} \]
把第一个等式右边的第一项挪到左边去,上下两个等式相除,可以得到,
\[ \phi_{j}\left(\gamma_{n}\right)=-\frac{B_{i j}}{A_{i j}}=\frac{\frac{k_{j}}{k_{j+1}} \tanh \left(\gamma_{n} t_{j}\right)+\phi_{j+1}\left(\gamma_{n}\right)+\frac{k_{j}}{h_{c j}} \gamma_{n} \phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)}{\frac{k_{j}}{k_{j+1}}+\phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)+\frac{k_{j}}{h_{c j}} \gamma_{n} \phi_{j+1}\left(\gamma_{n}\right)} \]
从最底层向最顶层逐层递归,可以得到热源层的扩展函数\(\phi_1({\gamma_n})\),由于对热源平面作傅里叶级数展开时,和\(\phi_1(\gamma_n)\)的具体形式无关,因此\(A_{i1}\)的形式并没有变化,只要把新的扩展函数带进去就可以了。
\(A_{ij}\)的处理方式是一样的, $$ \[\begin{aligned} A_{i j}&=A_{i, j-1}\left[\frac{\cosh \left(\gamma_{n} t_{j-1}\right)-\phi_{j-1}\left(\gamma_{n}\right) \sinh \left(\gamma_{n} t_{j-1}\right)}{\frac{k_{j}}{h_{c, j-1}} \gamma_{n} \phi_{j}\left(\gamma_{n}\right)+1}\right]\\ \end{aligned}\]$$
对于零阶项,此时一维热阻需要额外考虑考虑界面热阻, \[ \begin{aligned} A_{0 j}&=\frac{Q}{a b}\left(\frac{1}{h_{s}}+\sum_{l=j}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right)\\ B_{0 j}&=-\frac{Q}{a b k_{j}}\\ \end{aligned} \] 按照同样的递归方式,可以得到整个系统中的温度分布。
二维情况的对应解
整体思路都是一样的,扩展函数的形式也是一样的,只是傅里叶级数展开的形式有些差别,具体可以参考扩展热阻(2)-二维情况的解析解,这里直接给出结果。
通解形式
$$ \[\begin{aligned} \theta_{j}\left(x, z_{j}\right)=& A_{0 j}+B_{0 j} z+\sum_{m=1}^{\infty} A_{1 j}\cos \left(\lambda_{m} x\right)\left[ \cosh \left(\lambda_{m} z_{j}\right)- \phi_j(\lambda_m) \sinh \left(\lambda_{m} z_{j}\right)\right] \\ \phi_{N}\left(\lambda_{m}\right) &= -\frac{B_{i N}}{A_{i N}}=\frac{\frac{k_{N} \lambda_{m}}{h_{s}} \tanh \left(\lambda_{m} t_{N}\right)+1}{\frac{k_{N} \lambda_{m}}{h_{s}}+\tanh \left(\lambda_{m} t_{N}\right)} \\ A_{11} &= \frac{4 Q \sin \left(\frac{d \lambda_{m}}{2}\right) \cos \left(X_{c} \lambda_{m}\right)}{a d k_{1} \lambda_{m}^{2}\phi_1 \left(\lambda_{m}\right) } \\ \end{aligned}\]$$
热源平面的温度表达式为,
\[ \begin{aligned} \theta_{1}\left(x, 0\right) &= A_0 + \sum_{m=1}^{\infty} \cos(\lambda_m x) A_{11}\\ &= \frac{Q}{a}\left(\frac{1}{h_{s}}+\sum_{l=1}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right) + \sum_{m=1}^{\infty} \cos(\lambda_m x)\frac{4 Q \sin \left(\frac{d \lambda_{m}}{2}\right) \cos \left(X_{c} \lambda_{m}\right)}{a d k_{1} \lambda_{m}^{2}\phi_1 \left(\lambda_{m}\right) } \end{aligned} \]
热源区域的平均温度为,
\[ \begin{aligned} \bar{\theta}_s &= \frac{1}{d} \int_{X_c + \frac{d}{2}}^{X_c - \frac{d}{2}} A_0 + \sum_{m=1}^{\infty} \cos(\lambda_m x) A_{11} \mathrm{d}x \\ &= \frac{Q}{a}\left(\frac{1}{h_{s}}+\sum_{l=1}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right) + \sum_{m=1}^{\infty} \int_{X_c - \frac{d}{2}}^{X_c + \frac{d}{2}} \cos(\lambda_m x)\frac{4 Q \sin \left(\frac{d \lambda_{m}}{2}\right) \cos \left(X_{c} \lambda_{m}\right)}{a d k_{1} \lambda_{m}^{2}\phi_1 \left(\lambda_{m}\right) } \mathrm{d}x \\ &= \frac{Q}{a}\left(\frac{1}{h_{s}}+\sum_{l=1}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right) + \sum_{m=1}^{\infty} \frac{8 Q \sin ^{2}\left(\frac{d \lambda_m}{2}\right) \cos ^{2}\left(X_{c} \lambda_m\right)}{a d^2 k_{1} \lambda_m^{3} \phi_1(\lambda_m)} \end{aligned} \]
总热阻为,
\[ R_t = \bar{\theta}_s / Q \]
一维热阻为,
\[ R_{1D} = \frac{1}{a}\left(\frac{1}{h_{s}}+\sum_{l=1}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right) \]
扩展热阻为,
\[ R_s = \sum_{m=1}^{\infty} \frac{8 \sin ^{2}\left(\frac{d \lambda_m}{2}\right) \cos ^{2}\left(X_{c} \lambda_m\right)}{a d^2 k_{1} \lambda_m^{3} \phi_1(\lambda_m)} \]
从这里的分析可以看到,扩展函数只是级数的函数,与坐标无关。不同的扩展函数表达式对于基于温度的物理量的一般表达式没有影响。进而,每一层的扩展函数是固定的,\(A_ij\)也是固定的,虽然每个点的温度都要求一遍无穷级数,但是系数只需要每一层求一次。
无界面热阻
\[ \begin{aligned} \phi_{j}\left(\gamma_{n}\right)&=\frac{\frac{k_{j}}{k_{j+1}} \tanh \left(\gamma_{n} t_{j}\right)+\phi_{j+1}\left(\gamma_{n}\right)}{\frac{k_{j}} {k_{j+1}}+\phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)}\\ A_{i j}&=A_{i, j-1}\left[\cosh \left(\gamma_{n} t_{j-1}\right)-\phi_{j-1}\left(\gamma_{n}\right) \sinh \left(\gamma_{n} t_{j-1}\right)\right]\\ A_{0 j}&=\frac{Q}{a}\left(\frac{1}{h_{s}}+\sum_{l=j}^{N} \frac{t_{l}}{k_{l}}\right) \\ B_{0 j}&=-\frac{Q}{a k_{j}}\\ \end{aligned} \]
考虑界面热阻
\[ \begin{aligned} \phi_{j}\left(\gamma_{n}\right)&=\frac{\frac{k_{j}}{k_{j+1}} \tanh \left(\gamma_{n} t_{j}\right)+\phi_{j+1}\left(\gamma_{n}\right)+\frac{k_{j}}{h_{c j}} \gamma_{n} \phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)}{\frac{k_{j}}{k_{j+1}}+\phi_{j+1}\left(\gamma_{n}\right) \tanh \left(\gamma_{n} t_{j}\right)+\frac{k_{j}}{h_{c, j}} \gamma_{n} \phi_{j+1}\left(\gamma_{n}\right)}\\ A_{i j}&=A_{i, j-1}\left[\frac{\cosh \left(\gamma_{n} t_{j-1}\right)-\phi_{j-1}\left(\gamma_{n}\right) \sinh \left(\gamma_{n} t_{j-1}\right)}{\frac{k_{j}}{h_{c, j-1}} \gamma_{n} \phi_{j}\left(\gamma_{n}\right)+1}\right]\\ A_{0 j}&=\frac{Q}{a}\left(\frac{1}{h_{s}}+\sum_{l=j}^{N}\left[\frac{t_{l}}{k_{l}}+\frac{1}{h_{\mathrm{cl}}}\right]\right) \\ B_{0 j}&=-\frac{Q}{a k_{j}}\\ \end{aligned} \]
GaN-on-SiC HEMT
GaN-on-SiC HEMT
在芯片的实际制备过程中,先从晶体粉末生长晶体,把晶体切片抛光后制备衬底晶片。常用的PVT升华法制备衬底时,需要加热到2000℃左右,让固体粉末升华为气体,气体在籽晶表面凝华生长成衬底。显而易见,这种方案制备的衬底片一定会存在很多缺陷,将它直接用于功率器件制造时,性能和良率都是有问题的。因此在器件衬底的基础上,生长制备一层表面缺陷少,晶格排列整齐,表面形貌良好的外延层,将外延片用于制备功率器件。外延层消除了许多在晶体生长和其后的晶片加工中所引入的表面或近表面的缺陷,器件的参数稳定性和良率都会大幅提高。
GaN-on-SiC HEMT器件就是在SiC衬底上生长的GaN外延层器件,结合了SiC优异的导热性和的GaN高功率密度和低损耗的能力。模拟多层器件,分析其温升和热阻,这是一个很好的研究对象。

(Warzoha R J, Wilson A A, Donovan B F, et al. Applications and impacts of nanoscale thermal transport in electronics packaging[J]. Journal of Electronic Packaging, 2021, 143(2): 020804.)
GaN/SiC HEMT可以抽象为两层或者三层的简单结构,最上层为GaN外延层,中间为SiC衬底层,最下层为Die attach黏着层,把器件和热沉贴在一起,形成封装。

还是拿出一个Period来分析,
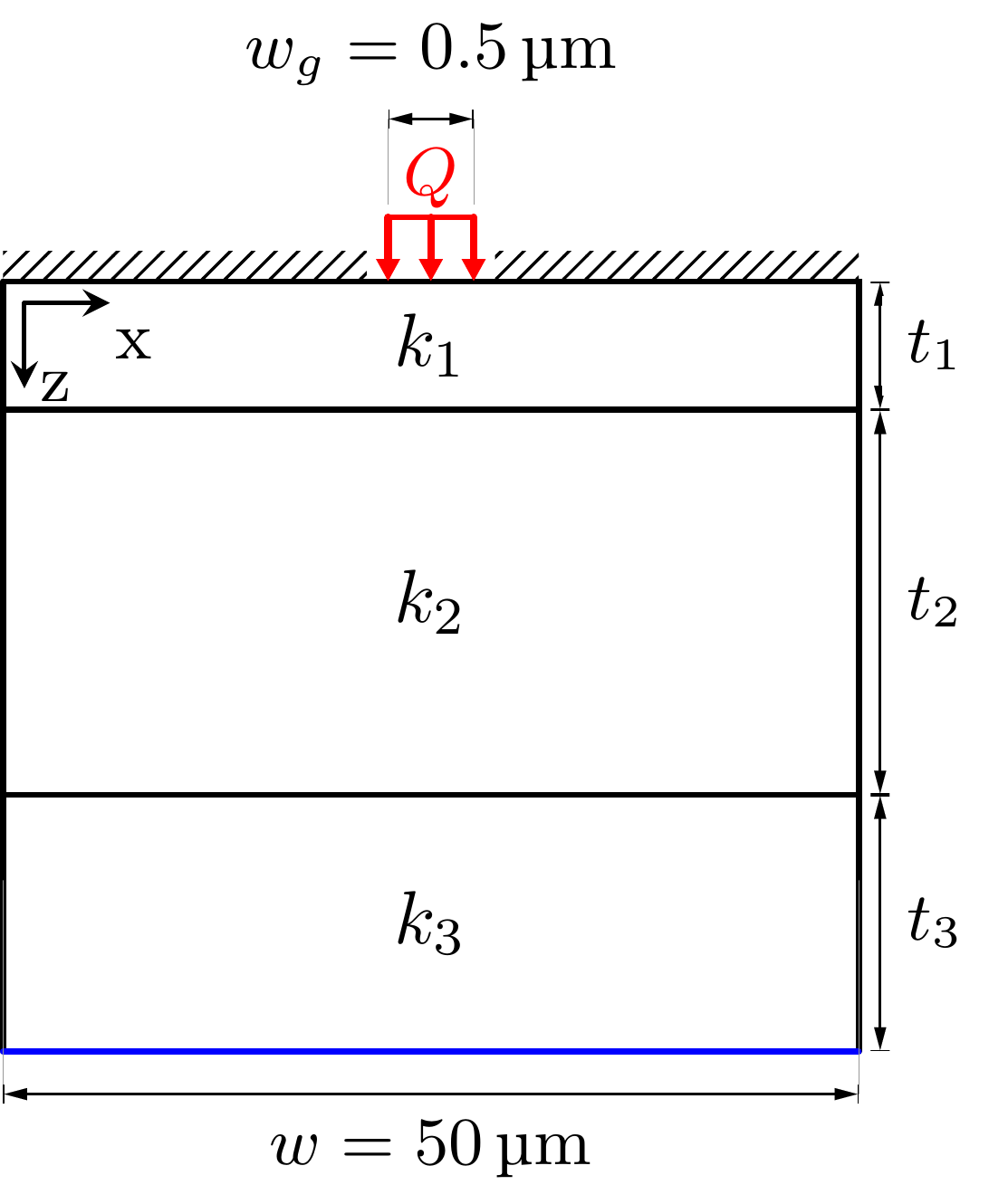
这里主要关注三个量,一个是体系的总热阻,一个是热源平面的温度分布,一个是热源中心线的温度分布。设第一层和第二层的界面热导为\(1\mathrm{e}^7 \, \mathrm{Wm^2/K}\),第二层和第三层间无界面热阻。
数值计算
不采用符号推导,用纯数值方案计算傅里叶级数时,一旦级数项稍微多一些,或者当深度\(z\)较大, \[
\sinh(\gamma_mt)=\frac{\mathrm{e}^{\gamma_m t} - \mathrm{e}^{-\gamma_m t}}{2}
\] 就会超过8位double类型的上限\(1.7E+308\),导致溢出。而处理这种热源宽度很窄的体系时,相当于作仿真要画至少比热源更窄的网格,解析解也需要更多的级数项才能保证收敛。这个时候需要对 \[
\cosh \left(\lambda_{m} z_{j}\right)- \phi_j(\lambda_m) \sinh \left(\lambda_{m} z_{j}\right)
\] 这一项做一些近似,在观察解的特征时,可以发现当\(\lambda_m\)较大时, \[
\phi_j(\gamma_m)\approx 1
\] 且\(z_j\)越大,\(\phi_j(\gamma_m)\)趋向于\(1\)的速度就越大。在热源平面层,级数到第\(93\)项时才满足 \[
1 - \phi_1(\gamma_{93}) < 1\mathrm{e}^{-10}
\] 而对于第二层或者第三层,在级数的第二项就成立了。在\(\phi_j(\gamma_m)\approx 1\)近似下,存在 \[
\cosh \left(\lambda_{m} z_{j}\right)- \phi_j(\lambda_m) \sinh \left(\lambda_{m} z_{j}\right) \approx \exp\left( -\gamma_n z_j \right)
\] 从而避免了指数发散。
1 | class SingleSpreading(object): |
结果
热源平面的温度分布,

\(x = 25\mathrm{\mu m}\)的温度分布,
