半导体载流子和高温激发

......约翰·斯图尔特·密尔（John Stuart Mill）曾抱怨：“我们徒劳地在工人阶层中寻找自尊，这会驱动他们选择以优秀的工作回报高薪，但在绝大多数情况下，单方面的善意被报以竭尽所能的偷懒。”他哀叹过去的工匠这么快就变成了工人，只剩下计算成本效益的冷漠，哀叹前工业时代的工匠本能如此迅速地消亡。颇为讽刺的是，市场理性腐蚀工人的奉献精神，对工作伦理的呼吁却遮蔽了昔日驱动工人远离市场理性的力量。工作伦理的幌子之下演化出一种纪律伦理：不用在意尊严或荣誉，感受或目的——全力工作就好，日复一日，争分夺秒，即使你完全看不到努力的意义所在。

在过去，工人通过自己设定目标、自己控制进程获得工作的意义和动力，但现在，他们只能被动地完成由他人设置和控制的任务，工作对他们而言失去了意义。在这种转变之下，如何驱动工人运用自己的技能完成这些没有意义的任务，是现代化的开拓者面临的真正问题。解决方案是机械地训练工人，让他们习惯于不假思索的盲从，并且剥夺他们完善工作的自豪感。如同维尔纳·桑巴特（Werner Sombart）所言，新的工厂系统需要的只是人的一部分：身处复杂机器之中，如同没有灵魂的小齿轮一样工作的那部分。这场战斗是为了对抗人身上那些无用的“部分”——兴趣和雄心，它们不仅与生产力无关，还会干扰生产需要的那些有用的“部分”。工作伦理本质上是对自由的摒弃。

1806年，一位佚名的针织品商人，生动地描述了这种披着“工作伦理”外衣的道德说教对于其目标群体的真正意义：

我发现人们对于任何规律性的安排有着极度的厌恶……他们非常不满意，因为他们不能随心所欲地出入，不能随心所欲地享受假期，不能按习惯的方式行事，下班之后还会遭受其他工人不怀好意的监视。这使得他们痛恨整个系统，我不得不将其打破。

就目的而言，工作伦理改革运动是一场关于控制和服从的战争。除名称以外，这是一场彻头彻尾的权力斗争，以崇高道德为名，迫使劳动者接受既不高尚，也不符合他们道德标准的生活。

---

……上层阶级希望劳动者只具有奴隶的价值。工人应该是勤勉的、专注的，永远不要考虑自己，只对主人忠诚，依附于主人，他们应该认识到自己在国家经济中最适当的地位就是过去种植园经济时代奴隶所处的地位。我们平时赞赏的人类美德，到了奴隶身上就成为了罪恶。

让人们平和地、不假思索地服从冷酷无情的机械化工厂工作的规劝之中，存在着一种奇怪的混合：本质上属于前工业时代、反现代的奴隶经济心态与一种大胆的新设想混合在一起。后者认为，一旦传统的束缚被打破，随着人们创造力的发展和对自然的掌控，呈现在人们面前的将是一个美好的、神奇的、丰富的世界。

​ <工作、消费主义和新穷人>，齐格蒙特·鲍曼

电子运动的基本规律

伟大的物理学家德布罗意告诉我们，任何一个实物粒子又同时是一种波，假如粒子的动量是\(\mathbf{p}\)，能量是\(E\)，那么这个粒子对应的波的波矢\(\mathbf{k}\)和角频率\(\omega\)则满足 \[ \mathbf{p} = \hbar\mathbf{k}, E = \hbar\omega \] 德布罗意关系告诉我们，我们不再能用传统的牛顿力学去预测粒子的运动了，而必须考虑到波的传播特性。为方便描述粒子运动，我们一般采用波包近似，波包是指局限在空间的某有限范围区域内的波，在其他区域的部分非常微小，可以被忽略，因此它的传播好像一小团弥散的粒子一样。我们用波包中心的坐标\(\mathbf{r_0}\)代表这个等效的粒子位置，用波包中心的动量代表粒子动量\(\hbar \mathbf{k_0}\)，实际上波包中粒子空间分布在波包中心\(\mathbf{r_0}\)附近的\(\Delta \mathbf{r}\)范围内，动量取值为波包动量中心\(\hbar\mathbf{k_0}\)附近的\(\hbar\Delta \mathbf{k}\)范围内，\(\Delta \mathbf{r_0}\)与\(\Delta \mathbf{k}\)满足测不准关系。在这种近似下，粒子可以被视为准经典的粒子，它有着经典的坐标和动量，但是坐标和动量的取值和更新方式，由波的性质决定。

波包的群速度，就是波包中心的移动速度，也就等同于准粒子的移动速度 \[ \mathbf{v}(\mathbf{k}) = \nabla_k \omega = \frac{1}{\hbar}\nabla_k E(k) \] 这个关系告诉我们，电子速度的方向为k空间中能量梯度的方向，即垂直于等能面。因此，电子的运动方向取决于等能面的形状。在一般情况下，k空间中的等能面并不是球面，因此，速度的方向一般并不是k的方向，只有当等能面为球面（自由电子），或在某些特殊方向上， v才与k的方向相同。电子状态\(k\)确定，则电子速度确定。

硅导带底部6个等价的椭球形等能面

在受到电场作用时， \[ \mathbf{F} = \frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = \hbar \frac{\mathrm{d}\mathbf{k}}{\mathrm{d}t} \] 于是 \[ \frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t} = \frac{1}{\hbar} \frac{\mathrm{d} \nabla_k E(k)}{\mathrm{d}t} = \frac{1}{\hbar} \sum_\beta \frac{d k_\beta}{\partial t} \frac{\partial}{\partial k_\beta}\left(\frac{\partial E(k)}{\partial k_\alpha}\right) = \frac{1}{\hbar^2} \sum_\beta F_\beta \cdot \frac{\partial^2}{\partial k_\beta \partial k_\alpha} E(k) \]

能带理论

根据上面的讨论，我们已经知道了，电子状态确定，则电子速度确定。也知道了给定状态的电子，在受到电场力后是如何运动的，那么我们只要知道实际半导体中，电子可取得的状态，就可以理解电子在半导体中的运动了。

从这个观点来看，历史上人类对于电子态的认识，大体上历经了三个阶段，德鲁德理论（经典的自由电子气模型），索末菲理论（量子化的自由电子气模型），和布洛赫理论（能带模型）。在德鲁德模型中，电子如同理想气体分子，遵循玻尔兹曼统计规律，E-k关系也自然是连续的抛物线分布；在索末菲模型中，通过求解自由电子薛定谔方程并引入周期性的波恩-卡门边界条件，发现电子可以取的态并不是连续的，而是一个个离散的态；更进一步，布洛赫通过引入周期性势场，发现此时在波函数布里渊区边界处会发生简并微扰，边界能级会发生突变，形成能带结构，属于一个布里渊区的能级构成一个能带，不同的布里渊区的能级对应不同的能带。电子可以取到的态，只能位于能带中，而禁带中是不允许存在的。

费米-狄拉克统计

通过能带模型，我们已经知道了电子态在半导体里是怎么分布的了，那么电子是怎么填充到这些态里的呢？于是根据泡利不相容原理推导的费米-狄拉克分布出现了， \[ f(\epsilon_i) = \frac{1}{e^{(\epsilon_i - \mu) /k_BT} + 1} \] 其中\(\mu\)是化学势，在半导体中，也被称为费米能级。费米分布告诉了我们一个电子填充到能量为\(\epsilon_i\)的态上的概率，如下图所示。

假设处于绝对零度，那么高过费米能级的态上有电子填充的概率为0，低于费米能级的态上有电子填充的概率为1。于是此时材料中的电子状态由最低能级依次向上填充，恰好填到某一个能带填满，下一个能带全空，电子填充的最高能级，就被称为费米能级。此时被填满的能带被称为满带，如下图的红色区域，满带中能量最高的带称为价带。费米能级的标准定义是这样，实际上在现实场合中，绝对零度根本不可能达到，那么我们怎么确定费米能级呢？根据费米分布可以发现，当能量等于费米能级的时候，填充概率为1/2。于是在实际半导体里它只是一个统计概念了，用来参考能带上某个位置被电子填充的概率，我们一般是通过载流子的浓度来确定费米能级的位置，而不是通过费米能级来计算载流子浓度。

在满带中，由于电子已经占据了所有能级，因此电子无法发生运动，因此满带是不导电的。这一点可以结合前面讨论的德布罗意关系+能带理论+费米-狄拉克分布来理解。只要电子的态确定了，电子的速度就确定了，因此电子在固体中的运动，实际上相当于电子在一系列离散的态之间跳跃。而由于同一个态上最多只能填充一个电子，电子从一个态跳跃到另一个态，必然有另一个电子从对应的态跳回来，这样电子运动恰好抵消，晶体中净电流为0。声子满足的玻色分布就不一样了，由于没有泡利不相容原理的限制，一个态上填充多少个声子都行，声子同时又不受力，所以它的理论要简单许多。

对于导体来说，它根本就没有禁带，导带和价带直接重合了，所以电子始终可以在非满的导带中运动。对于半导体来说，导带和价带间的禁带宽度并不是太大，因此在温度大于绝对零度的情况下，一部分电子会因为热运动的激发跳跃到非满的导带中，此时价带中有留下了相等数目的带正电的空穴，他们是可以导电的；而对于绝缘体来说，禁带宽度太大，基本上不会有电子有足够的能量跳跃到导带，无法导电。

载流子激发

通过前面的讨论我们已经知道了，想让半导体导电，就得让电子从满的价带，跳跃到不满的导带上。导带比价带能量高，所以我们将这种跳跃，称作激发。半导体中主要存在两种激发方式，分别是本征激发和杂质激发。

当温度较高时，电子受热运动从价带跃迁到导带，同时产生价带的空穴和导带的电子，空穴数目等于电子数目，我们将这种电子和空穴统称为本征载流子能级。在\(E - E_F \gg k_BT\)时，费米分布退化为玻尔兹曼分布，此时导带中的电子浓度可以表示为 \[ n = \int_{E_c}^{\infty} N_c(E) f(E) = \int_{E_c}^{\infty} \frac{(2m_c^*)^{3/2}}{2\pi^2\hbar^3}\sqrt{E - E_c} \exp(- \frac{E - E_F}{k_BT}) \mathrm{d}E = 2 \left(\frac{m_c^*k_BT}{2\pi\hbar^2}\right)^{3/2} \exp(- \frac{E_c - E_F}{k_BT}) \] 把\(N_c = 2 \left(\frac{m_ck_BT}{2\pi\hbar^2}\right)^{3/2}\)称为导带的有效状态密度，这个表达式表明在计算导带电子数时可以等效地用导带底部能级\(E_c\)来代替整个导带，导带的电子数就如同在导带底\(E_c\)处集中了\(N_c\)个能态所含有的电子数。这个意思是说，电子可以存在的态还是一个一个离散的，这样的态共有\(N_c\)个，但是这些态的能量都是\(E_c\)。空穴浓度也有着类似的表达式， \[ p = 2 \left(\frac{m_v^*k_BT}{2\pi\hbar^2}\right)^{3/2} \exp(- \frac{E_F - E_v}{k_BT}) \] 把\(N_v = 2 \left(\frac{m_vk_BT}{2\pi\hbar^2}\right)^{3/2}\)称作价带的有效状态密度。两种载流子的浓度乘积，满足 \[ np = N_c N_v \exp(- \frac{E_g}{k_B T}) \] 半导体中两种载流子浓度的乘积是一个仅与禁带宽度\(E_g\)和温度有关的量，而与半导体的费米能级\(E_F\)无关。在一定温度下，导带中的电子越多，价带中的空穴就越少。导带电子、价带空穴和浓度乘积的关系表达式是半导体处于热平衡时的普遍表达式，不论是本征半导体还是掺杂半导体，都同样适用，因为导带位置基本不会变，掺杂相当于引入了距离导带更近的杂质能级，杂质能级上电子更容易激发到导带中。那么掺杂相当于改变了什么呢？相当于改变了材料的费米能级\(E_F\)。

半导体中另一种载流子激发方式是杂质激发，以N型半导体为例，通过在本征半导体中引入五价元素，如P和As等，这些原子本身就带有5个价电子，热运动断掉一个键以后，外层电子刚好填满，没有空位，因此不会产生空穴，导致电子数目会大大高于空穴数目。而对于本征半导体比如Si，它有4个键，断掉一个后，产生一个自由电子，空出一个位置，就会留下一个空穴，因此本征半导体中电子数目和空穴数目是相等的。

对于浅掺杂，掺杂能级靠近导带，杂质能级对电子的束缚能很小，电子很容易从施主能级跃迁到导带。大部分情况下，我们可以认为掺杂的杂质全部发生电离，且在温度不太高时，电离出的自由电子浓度远大于本征载流子浓度，因此存在关系 \[ N_c \exp\left(- \frac{E_c - E_F}{k_BT}\right) = N_D \] 解得费米能级为 \[ E_F = E_c + k_BT\ln(\frac{N_D}{N_c}) \] 在一般掺杂浓度下，\(N_c > N_D\)，因此在一定温度时，掺杂浓度越高，费米能级\(E_F\)就越向导带靠近；而在掺杂浓度一定时，温度越高，本征载流子激发就越强，此时\(E_F\)就越向本征费米能级\(E_{Fi}\)靠近（无掺杂时的费米能级）。

载流子高温特性

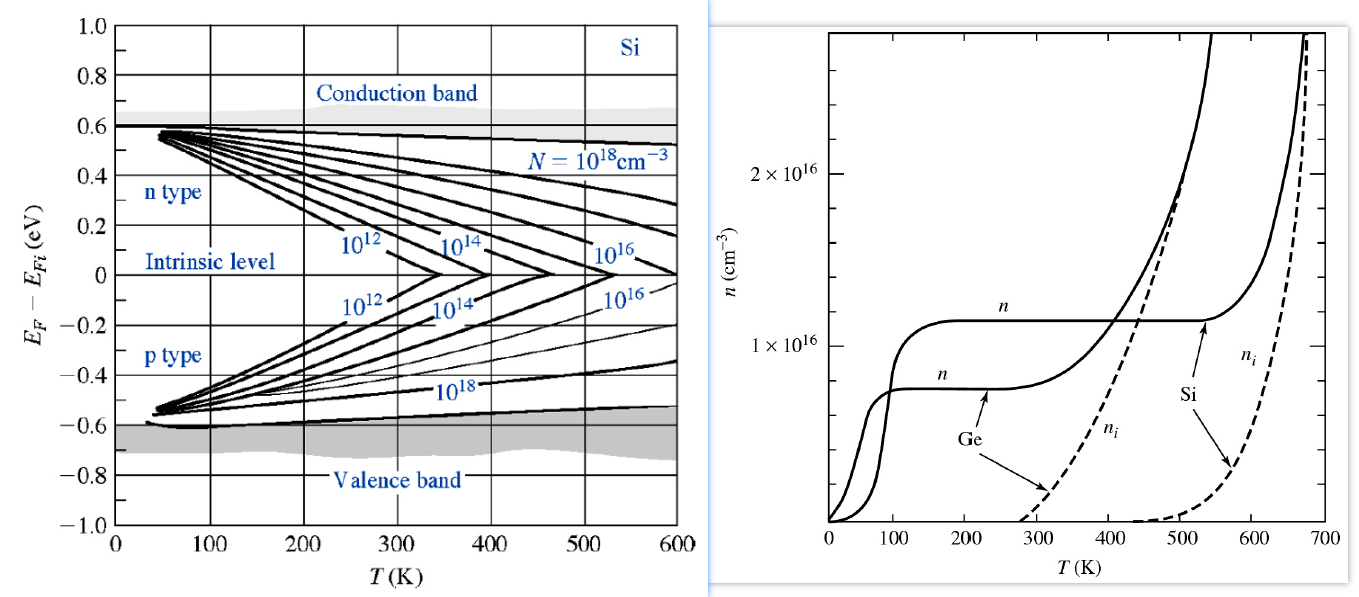
经常提到宽禁带半导体很适合在高温下工作，通过前面讨论的这些内容，就可以理解这件事情了。下面这两张图，左边展示了硅的费米能级与掺杂浓度和温度的关系，右边展示了N型硅和锗的电子浓度与温度的关系曲线。在低温段，载流子激发很少，费米能级高于杂质能级；在常温段，费米能级下降，低于杂质能级；在高温段，本征载流子激发增强，费米能级靠近本征费米能级，此时掺杂基本失效了。从右边这张图可以看到，对于硅，在低温时，电子浓度随着温度的升高而增加，因为此时杂质在逐渐电离。温度升高到100K时，杂质全部电离，此时电子浓度基本保持不变，而当温度高于500K时，本征激发开始起主要作用，此时掺杂就失效了，器件也就没用了。显然，杂质浓度越高，达到本征激发起主要作用的温度也就越高。对于锗来说，它的禁带宽度更小，所以在常温下，也很难阻止它的本征激发，所以在人类的世界里，锗材料并没有被广泛使用。

所以为什么宽禁带半导体适合在高温场合下应用？因为本征载流子浓度为 \[ n_i = n = p = (N_c N_p)^{1/2} \exp(- \frac{E_g}{2k_BT}) \] 带隙越宽，本征载流子就越难激发，理论最大容许温度就越高。所以对硅来说，在一般掺杂的情况下300℃就是极限了，而SiC的理论极限工作温度可以达到800℃。这个温度并没有考虑器件的可靠性，实际上SiC器件在200℃左右的结温下就会发生热失控问题，而硅器件可能结温达到175℃左右也会发生可靠性和性能下降问题。